Matriks segitiga atas dan bawah

Pada halaman ini Anda akan melihat apa itu matriks segitiga dan macam-macam matriks segitiga beserta contohnya. Selain itu, Anda akan mengetahui cara menghitung determinan matriks segitiga dan apa saja sifat-sifat matriks yang sangat menarik ini. Terakhir, kami juga akan menjelaskan apa itu matriks Hessenberg, karena merupakan matriks yang berkaitan dengan matriks segitiga.

Apa itu matriks segitiga?

Definisi matriks segitiga:

Matriks segitiga adalah matriks persegi yang semua elemen di atas atau di bawah diagonal utamanya bernilai nol (0).

Matriks segitiga banyak digunakan dalam perhitungan aljabar linier, karena membalikkan matriks segitiga, menghitung determinannya, atau bahkan menyelesaikan sistem persamaan linier dengan matriks jenis ini jauh lebih mudah dibandingkan dengan matriks yang memiliki elemen selain 0 di semua posisi. .

matriks segitiga atas

Matriks segitiga atas adalah matriks persegi yang elemen-elemen di bawah diagonal utamanya bernilai nol (0).

Contoh matriks segitiga atas:

matriks segitiga bawah

Matriks segitiga bawah adalah matriks persegi yang mempunyai angka nol (0) pada setiap elemennya yang berada di atas diagonal utama.

Contoh matriks segitiga bawah:

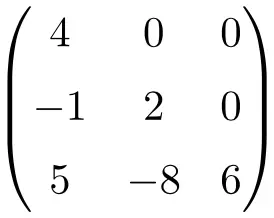
Kadang-kadang matriks ini disebut juga dengan huruf U, untuk matriks segitiga atas, dan dengan huruf L, untuk matriks segitiga bawah. Meskipun tata nama ini terutama digunakan dalam bahasa Inggris, sebenarnya U adalah singkatan dari matriks segitiga atas dan L adalah matriks segitiga bawah .

Contoh matriks segitiga

Matriks segitiga 2×2 dimensi

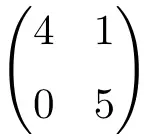
Matriks segitiga berorde 3×3

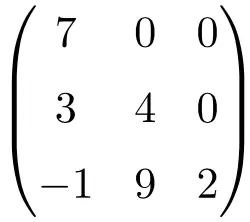
matriks segitiga berukuran 4×4

Penentu matriks segitiga

Penentu matriks segitiga , baik segitiga atas maupun bawah, adalah hasil kali elemen-elemen pada diagonal utama.

Perhatikan latihan berikut untuk menyelesaikan cara menghitung perkalian elemen-elemen diagonal utama matriks segitiga dengan cukup untuk mencari determinannya:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Teorema ini mudah ditunjukkan: cukup hitung determinan matriks segitiga dengan blok (atau kofaktor). Demonstrasi ini dirinci di bawah ini menggunakan matriks segitiga umum:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Sebaliknya, kita mengetahui bahwa suatu matriks dapat dibalik jika determinannya berbeda dengan 0. Jadi, jika tidak ada elemen pada diagonal utama yang bernilai 0, maka matriks segitiga tersebut juga dapat dibalik dan akibatnya menjadi matriks beraturan. matriks.

Sifat-sifat matriks segitiga

Sekarang mari kita lihat apa saja sifat-sifat matriks segitiga:

Hasil kali dua matriks segitiga atas sama dengan satu matriks segitiga atas. Dan sebaliknya: mengalikan dua matriks segitiga bawah menghasilkan matriks segitiga bawah lainnya.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

Transpos matriks segitiga atas adalah matriks segitiga bawah, dan sebaliknya: transpos matriks segitiga bawah adalah matriks segitiga atas.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Suatu matriks segitiga dapat dibalik jika semua elemennya pada diagonal utama bukan nol, yaitu jika berbeda dari nol. Dalam hal ini, invers matriks segitiga atas (bawah) juga merupakan matriks segitiga atas (bawah).

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Selain itu, diagonal utama matriks terbalik akan selalu memuat invers elemen diagonal utama matriks segitiga asal.

Setiap matriks diagonal merupakan matriks segitiga atas dan matriks segitiga bawah, misalnya:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Jadi matriks skalar juga merupakan matriks segitiga atas dan bawah. Misalnya matriks identitas:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Jelasnya matriks nol juga merupakan matriks segitiga atas dan bawah, karena elemen-elemen di atas dan di bawah diagonal utama adalah 0:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Nilai eigen (atau nilai eigen) suatu matriks segitiga adalah elemen diagonal utama.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Matriks segitiga atas atau bawah selalu mampu melakukan diagonalisasi berdasarkan vektor eigen (atau vektor eigen).

Matriks apa pun dapat difaktorkan menjadi hasil kali matriks segitiga bawah dan matriks segitiga atas . Artinya, matriks apa pun dapat diubah menjadi perkalian matriks segitiga. Selain itu, jika matriksnya dapat dibalik, transformasi ini bersifat unik. Untuk memfaktorkan suatu matriks, metode dekomposisi LU sering digunakan.

Melakukan segitiga pada suatu matriks

Ada beberapa teorema tentang matriks yang dapat ditriangularkan dengan mengubah alasnya. Namun, di sini kita akan melihat cara melakukan triangulasi suatu matriks dengan menerapkan transformasi elementer pada garis , seperti pada metode Gauss.

Misalnya:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

Dan dengan cara ini, kita telah membuat segitiga matriks aslinya.

Ingatlah bahwa transformasi dasar yang diotorisasi antar garis dalam metode Gaussian adalah:

Gantikan sebuah garis dengan kombinasi linier dari garis-garis lainnya.
Kalikan atau bagi semua suku dalam satu baris dengan angka selain 0.
Edit baris pesanan.

Matriks Hessenberg

Pengertian matriks Hessenberg adalah sebagai berikut:

Matriks Hessenberg merupakan matriks yang “hampir” berbentuk segitiga, artinya semua elemennya bernilai nol mulai dari subdiagonal pertama (matriks Hessenberg atas) atau superdiagonal pertama (matriks Hessenberg bawah).

Saya yakin ini paling baik dipahami dengan contoh matriks Hessenberg atas dan contoh matriks Hessenberg bawah lainnya:

Matriks Hessenberg Atas

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Matriks Hessenberg Bawah

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Matriks yang merupakan matriks Hessenberg atas dan bawah merupakan matriks tridiagonal .

Nama matriks ini diambil dari nama Karl Hessenberg, seorang insinyur dan matematikawan terkemuka Jerman abad ke-20.

Terakhir, matriks jenis ini memiliki kekhasan yaitu jika dikalikan dengan matriks segitiga maka hasilnya selalu berupa matriks Hessenberg.