Matriks hermitian (atau hermitian).

Di halaman ini Anda dapat mempelajari apa itu matriks Hermitian, yang juga dikenal sebagai matriks Hermitian. Anda akan menemukan contoh matriks Hermitian, semua sifat dan bentuk matriks jenis ini untuk memahaminya dengan sempurna. Terakhir, kami juga menjelaskan cara menguraikan matriks kompleks apa pun menjadi jumlah matriks Hermitian ditambah matriks anti-Hermitian.

Apa itu matriks Hermitian atau Hermitian?

Matriks Hermitian atau disebut juga matriks Hermitian adalah matriks persegi dengan bilangan kompleks yang mempunyai sifat sama dengan transpos konjugasinya.

A=A^*

Emas

A^*

adalah matriks transpos konjugat dari

A

.

Karena penasaran, matriks jenis ini dinamai untuk menghormati Charles Hermite, seorang matematikawan Perancis abad ke-19 yang melakukan penelitian penting di bidang matematika, khususnya di bidang aljabar linier.

Alasan penamaan matriks ini dengan cara ini adalah karena menunjukkan bahwa nilai eigen (atau nilai eigen) dari matriks tertentu selalu berupa bilangan real, namun kami akan menjelaskannya lebih detail di Sifat-sifat Matriks Hermitian.

Terakhir, matriks ini terkadang juga dapat disebut sebagai matriks adjoint mandiri, meskipun hal ini sangat jarang terjadi.

Contoh matriks Hermitian

Setelah kita melihat definisi matriks Hermitian (atau matriks Hermitian), mari kita lihat beberapa contoh matriks Hermitian dengan dimensi berbeda:

Contoh matriks Hermitian berorde 2×2

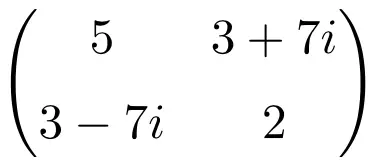
Matriks Hermitian atau Hermitian berdimensi 2x2

Contoh matriks Hermitian berdimensi 3×3

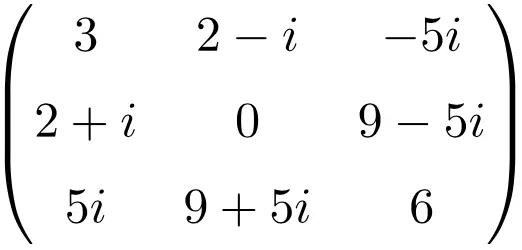
Matriks Hermitian atau Hermitian berdimensi 3x3

Contoh matriks Hermitian berukuran 4×4

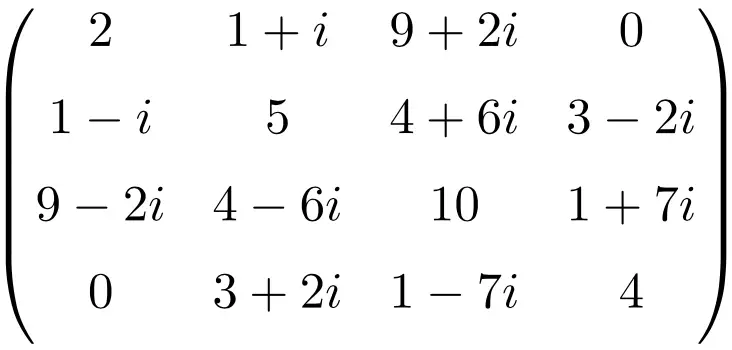
Matriks Hermitian atau Hermitian berdimensi 4x4

Semua matriks ini bersifat Hermitian karena matriks transpos konjugasinya masing-masing sama dengan matriks itu sendiri.

Struktur matriks Hermitian

Matriks Hermitian memiliki struktur yang sangat mudah diingat: matriks tersebut terdiri dari bilangan real pada diagonal utama, dan elemen kompleks yang terletak pada baris ke-i dan kolom ke-j harus merupakan konjugasi dari elemen yang terdapat pada baris ke-j dan kolom ke-i.

Berikut beberapa contoh struktur matriks Hermitian.

Struktur pertapa 2×2

\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}

Struktur pertapa 3×3

\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}

Struktur pertapa 4×4

\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}

Sifat-sifat matriks Hermitian

Sekarang kita akan melihat apa saja sifat-sifat matriks kompleks persegi jenis ini:

  • Setiap matriks Hermitian adalah matriks normal . Meskipun tidak semua matriks normal merupakan matriks Hermitian.
  • Matriks Hermitian apa pun dapat didiagonalisasi. Selanjutnya matriks diagonal yang dihasilkan hanya mengandung unsur nyata.
  • Oleh karena itu, nilai eigen (atau nilai eigen) matriks Hermitian selalu berupa bilangan real. Properti ini ditemukan oleh Charles Hermite, dan karena alasan ini dia mendapat kehormatan untuk menyebut matriks yang sangat istimewa ini Hermitian.
  • Demikian pula, ruang eigen matriks Hermitian adalah ortogonal dua per dua: terdapat basis ortonormal dari

    \mathbb{C}^n

    terdiri dari vektor eigen (eigenvector) dari matriks.

  • Suatu matriks bilangan real, artinya tidak ada unsur yang mempunyai bagian imajiner, adalah matriks Hermitian jika dan hanya jika matriks tersebut simetris. Seperti misalnya matriks identitas 2×2 .
  • Matriks Hermitian dapat dinyatakan sebagai jumlah dari matriks simetris nyata dan matriks antisimetri imajiner.

A =B+Ci

  • Jumlah (atau pengurangan) dua matriks Hermitian sama dengan matriks Hermitian lainnya, karena:

(A\pm B)^* = A^*\pm B^* = A \pm B

  • Hasil perkalian matriks Hermitian dengan skalar adalah matriks Hermitian lain jika skalarnya bilangan real.

(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A

  • Hasil kali dua matriks Hermitian umumnya bukan lagi matriks Hermitian. Akan tetapi, hasil perkaliannya adalah Hermitian jika kedua matriks tersebut dapat diubah, yaitu jika hasil perkalian kedua matriks tersebut sama terlepas dari arah perkaliannya, karena maka kondisi operasi dengan transpos konjugasi berikut matriks:

(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B

  • Jika matriks Hermitian dapat dibalik, maka inversnya juga merupakan matriks Hermitian.

(A^{-1})^* = (A^*)^{-1} = A^{-1}

  • Penentu matriks Hermitian selalu ekuivalen dengan bilangan real. Inilah bukti properti ini:

det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}

Haus

A = A^*

:

det(A) = \overline{det(A)}

Oleh karena itu, agar kondisi ini terpenuhi, determinan matriks Hermitian harus berupa bilangan real. Dengan cara ini, konjugasi hasilnya sama dengan hasil itu sendiri.

Penguraian matriks kompleks menjadi matriks Hermitian dan matriks anti-Hermitian

Setiap matriks dengan elemen kompleks dapat diuraikan menjadi jumlah matriks Hermitian ditambah matriks anti-Hermitian lainnya . Namun untuk ini Anda perlu mengetahui kekhasan dari jenis matriks berikut ini:

  • Jumlah matriks kompleks persegi ditambah konjugatnya yang ditransposisi menghasilkan matriks Hermitian.

C + C^* = \text{Matriz Hermitiana}

  • Perbedaan antara matriks kompleks persegi dan konjugat transposisinya menghasilkan matriks anti-Hermitian (atau anti-Hermitian).

C - C^* = \text{Matriz Antihermitiana}

  • Oleh karena itu, semua matriks kompleks dapat diuraikan menjadi jumlah matriks Hermitian dan matriks anti-Hermitian. Teorema ini dikenal sebagai dekomposisi Teoplitz :

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Dimana C adalah matriks kompleks yang ingin kita dekomposisi, C* adalah konjugat yang ditransposisikan, dan terakhir A dan B masing-masing adalah matriks Hermitian dan anti-Hermitian yang menjadi tempat dekomposisi matriks C.

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top