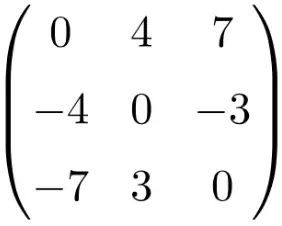Pada halaman ini kami menjelaskan apa itu matriks persegi dan Anda akan menemukan contoh matriks persegi. Selain itu, Anda akan melihat properti apa saja yang dimiliki matriks persegi, operasi yang dapat dilakukan dengannya, dan berbagai jenis yang ada.
Apa itu matriks persegi?
Matriks persegi adalah a matriks yang jumlah barisnya sama dengan jumlah kolomnya.
Contoh matriks persegi
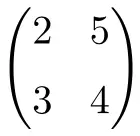
matriks persegi orde 2
matriks persegi orde 3
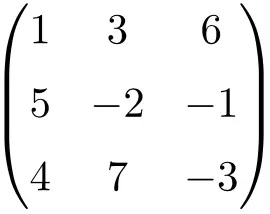
matriks persegi orde 4
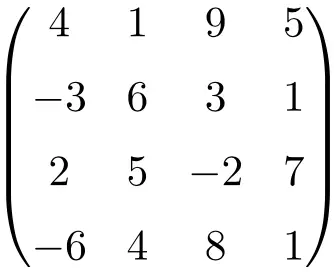
Seperti yang Anda lihat, matriks persegi biasanya diberi nama berdasarkan ordonya, yaitu matriks persegi berorde 2 berarti matriks tersebut berdimensi 2×2 (2 baris dan 2 kolom), atau kita menyebutnya matriks persegi berorde 3 yang menandakan ukurannya 3×3 (3 baris dan 3 kolom).
Diagonal matriks persegi
Diagonal-diagonal matriks persegi mempunyai nama tertentu, yaitu diagonal utama dan diagonal sekunder:
- Diagonal utama matriks persegi terdiri dari elemen-elemen yang bergerak dari sudut kiri atas ke sudut kanan bawah:

- Diagonal sekunder matriks persegi sesuai dengan elemen-elemen yang bergerak dari sudut kiri bawah ke sudut kanan atas:

Sifat-sifat matriks persegi
Matriks persegi banyak digunakan dalam aljabar linier, itulah sebabnya matriks persegi sangat penting. Jadi mari kita lihat ciri-ciri apa yang membuat kelas matriks ini begitu relevan:
- Matriks persegi apa pun dapat diuraikan menjadi jumlah matriks simetris dan matriks antisimetris .
- Jika dua matriks persegi berordo sama, maka matriks-matriks tersebut dapat dijumlahkan atau dikurangkan satu sama lain:
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- Dua matriks persegi dapat dikalikan pada kedua arah yang memungkinkan. Namun hasil kali matriks persegi tidak bersifat komutatif, yaitu hasil perkaliannya akan berubah tergantung pada sisi mana matriks tersebut dikalikan. Perhatikan pada contoh berikut bagaimana hasilnya bergantung pada posisi matriks:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- Matriks persegi adalah satu-satunya matriks yang dapat menghitung determinannya. Oleh karena itu, suatu determinan hanya dapat diselesaikan jika matriks tersebut berbentuk persegi. Misalnya, untuk mencari determinan matriks persegi 3×3, Anda harus menerapkan aturan Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
Ingat juga bahwa jika determinan suatu matriks berbeda dengan 0, berarti matriks tersebut adalah matriks beraturan , yaitu matriks yang dapat dibalik. Sebaliknya, jika determinannya nol, maka matriks tersebut merupakan matriks singular (yang tidak memiliki invers).
- Akhirnya matriks persegi dapat didiagonalisasi . Dengan demikian perubahan basis dapat dilakukan untuk menghitung nilai eigen (atau nilai eigen) dan vektor eigen (atau vektor eigen) suatu matriks persegi.
Operasi dengan matriks persegi
Seperti yang telah kita ketahui, determinan suatu matriks hanya dapat dihitung jika matriks tersebut berbentuk persegi. Demikian pula, ada juga operasi tertentu yang hanya dapat dilakukan jika matriksnya berdimensi persegi:
jejak suatu matriks
Jejak suatu matriks adalah jumlah elemen-elemen yang membentuk diagonal utama suatu matriks persegi.
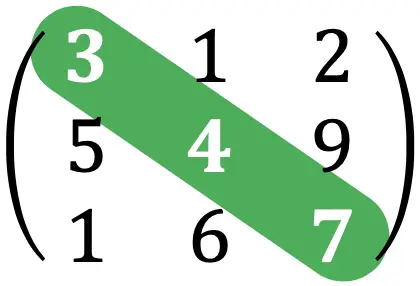
Misalnya, jejak matriks dari latihan di atas adalah:
![]()
Jenis cetakan persegi
Maka Anda memiliki jenis matriks persegi terpenting yang ada. Klik pada jenis dadu untuk mengetahui apa yang istimewa darinya.
Seperti yang Anda lihat, ada banyak jenis matriks persegi, dan masing-masing matriks memiliki namanya sendiri karena alasan yang berbeda.