Matriks involusional

Di halaman ini Anda akan mempelajari apa itu matriks involusi. Kami juga menunjukkan contoh matriks involutif berdimensi 2×2, 3×3, dan 4×4. Dan terakhir, Anda akan menemukan rumus matriks involusional.

Apa itu matriks involusional?

Arti dari matriks involusional adalah sebagai berikut:

Pengertian matriks involutif : Suatu matriks persegi yang dapat dibalik yang matriks inversnya adalah matriks itu sendiri.

$A^{-1} = A$

Emas

$A$

adalah matriks apa pun dan

$A^{-1}$

mewakili kebalikannya.

Jadi jelas matriks involusional merupakan contoh matriks beraturan atau matriks tak berdegenerasi .

Jika anda belum mengetahui apa itu invers suatu matriks, disini anda bisa melihat cara menghitung invers matriks 3×3 . Penting untuk mengetahui cara membalikkan matriks, namun untuk ini Anda juga perlu mengetahui cara menghitung adjoint suatu matriks .

Namun kembali ke pokok bahasan: ketika suatu matriks bersifat involutif, perkalian matriks dengan matriks itu sendiri menghasilkan matriks identitas. Lihatlah demonya:

Setiap matriks dikalikan dengan inversnya menghasilkan matriks Identitas (atau Unit). JADI:

$\displaystyle A \cdot A^{-1} = I$

Dan karena invers dari matriks involusi adalah matriks itu sendiri:

$\displaystyle A \cdot A = I$

Akibatnya, matriks involusi kuadrat menghasilkan matriks identitas:

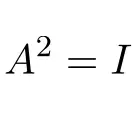
Contoh matriks involusional

Contoh matriks involusi 2×2:

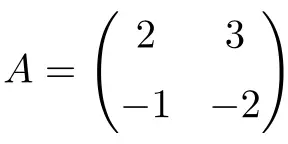
Kita dapat memverifikasi bahwa ini adalah matriks involusional dengan menghitung pangkat kedua dari matriks tersebut:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Karena matriks A kuadrat adalah matriks identitas, maka matriks A adalah matriks involusional 2×2.

Contoh matriks involusi 3×3:

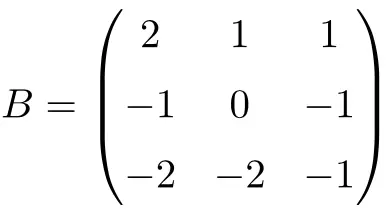
Kita dapat memverifikasi bahwa ini adalah matriks involusional dengan menyelesaikan perkalian matriks itu sendiri:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Karena matriks B kuadrat adalah matriks identitas, maka matriks B adalah matriks involusional 3×3.

Contoh matriks involusi 4×4:

Matriks Identitas (atau Unit), apa pun dimensinya, menurut definisinya adalah matriks involusional.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Kita dapat memverifikasi bahwa ini adalah matriks involusional dengan menaikkan matriks menjadi 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Karena matriks identitas kuadrat adalah matriks identitas, maka matriks identitas tersebut merupakan matriks involusi 4×4.

Tentu saja matriks identitas dapat berdimensi apa saja, karena matriks tersebut hanyalah sebuah matriks diagonal dengan semua angka 1 pada diagonal utama dan sisanya 0. Jadi matriks identitas akan selalu berupa matriks involusional, apapun ordenya.

Rumus matriks yang melibatkan

Salah satu sifat matriks involusi adalah dapat diketahui rumusnya. Namun pembuktian rumus matriks involusi orde kedua cukup membosankan, jadi langsung saja kita lihat hasilnya, itu yang penting. Jika Anda lebih tertarik dengan demonya, Anda dapat melihatnya dijelaskan langkah demi langkah di bawah di komentar.

Rumus matriks involutif berdimensi 2 × 2 adalah sebagai berikut:

Oleh karena itu, setiap matriks yang nilai diagonal utamanya berlawanan dan determinannya -1, akan menjadi matriks involusional.

Namun, selain matriks yang dijelaskan oleh rumus ini, harus diperhatikan bahwa matriks identitas dan kebalikannya juga merupakan matriks involusional berorde 2:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Sifat-sifat matriks involusi

Matriks involusional mempunyai ciri-ciri sebagai berikut:

Penentu matriks involusional selalu sama dengan -1 atau +1.

Ada hubungan antara matriks involusional dan matriks idempoten : matriks
$A$

bersifat involusional jika dan hanya jika matriksnya

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

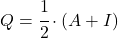
adalah idempoten.

Ya
$A$

Dan

$B$

adalah dua matriks involusi komutasi , lalu hasil kali matriks

$AB$

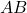
juga merupakan matriks involusional lainnya.

Kekuatan apa pun dari matriks involusional akan menghasilkan matriks involusional lainnya. Secara khusus, matriks involusional yang dipangkatkan ganjil akan sama dengan matriks itu sendiri, sebaliknya jika dipangkatkan ke eksponen genap maka akan ekuivalen dengan matriks Identitas.

$A^2 = I$

$A^3 = A$