Matriks Hessian (atau Hesse) -

Halaman ini tentunya merupakan penjelasan terlengkap tentang matriks Hessian yang ada. Disini dijelaskan konsep matriks Hessian, cara menghitungnya beserta contohnya bahkan ada beberapa soal soal yang bisa dipraktekkan. Selain itu, Anda akan dapat mempelajari cara menghitung nilai maksimum dan minimum suatu fungsi multivariabel, serta apakah fungsi tersebut cekung atau cembung. Dan terakhir, Anda juga akan menemukan utilitas dan aplikasi matriks Hessian.

Apa itu matriks Hessian?

Pengertian matriks Hessian (atau Hessian) adalah sebagai berikut:

Matriks Hessian adalah matriks persegi berdimensi n × n yang tersusun dari turunan kedua parsial suatu fungsi n variabel.

Matriks ini disebut juga dengan nama Hessian, atau bahkan di beberapa buku matematika dinamakan Diskriminan. Namun cara paling umum untuk menyebutnya adalah matriks Hessian.

Oleh karena itu, rumus matriks Hessian adalah sebagai berikut:

Oleh karena itu, matriks Hessian akan selalu berupa matriks persegi yang dimensinya sama dengan jumlah variabel dalam fungsinya. Misalnya fungsi memiliki 3 variabel, maka matriks Hessian akan berdimensi 3×3.

Selain itu, teorema Schwarz (atau teorema Clairaut) mengatakan bahwa urutan diferensiasi tidak menjadi masalah, yaitu turunkan sebagian terlebih dahulu terhadap variabel

$x_1$

kemudian sehubungan dengan variabel

$x_2$

berarti melakukan diferensiasi parsial terhadap

$x_2$

lalu hormat

$x_1$

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

Oleh karena itu, matriks Hessian merupakan matriks simetris , atau dengan kata lain mempunyai simetri yang sumbunya merupakan diagonal utamanya.

Yang menarik, matriks Hessian dinamai Ludwig Otto Hesse, seorang matematikawan Jerman abad ke-19 yang memberikan kontribusi sangat penting dalam bidang aljabar linier.

Contoh penghitungan matriks Hessian

Mari kita lihat contoh cara mencari matriks Hessian berdimensi 2 × 2:

Hitung matriks Hessian di titik (1,0) dari fungsi berikut:

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

Pertama, kita perlu menghitung turunan parsial orde pertama:

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

Setelah kita mengetahui turunan pertama, kita menghitung semua turunan parsial orde kedua:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

Oleh karena itu, sekarang kita dapat mencari matriks Hessian dari rumus matriks 2 × 2:

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

Jadi matriks Hessian yang dievaluasi pada titik (1,0) adalah:

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

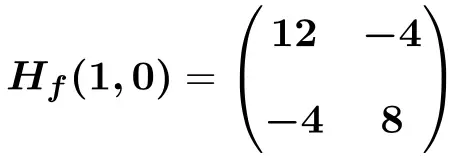
Memecahkan masalah matriks Hessian

Latihan 1

Hitung matriks Hessian dari fungsi berikut dengan 2 variabel di titik (1,1):

$\displaystyle f(x,y)=x^2y+y^2x$

lihat solusi

Pertama, kita perlu mencari turunan parsial orde pertama dari fungsi tersebut:

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

Setelah kita menghitung turunan pertama, kita lanjutkan menyelesaikan semua turunan parsial orde kedua:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

Dengan demikian matriks Hessian didefinisikan sebagai berikut:

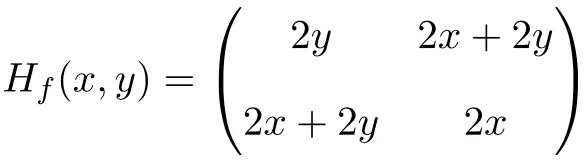
Latihan soal matriks Hessian atau Hessian berdimensi 2x2

Terakhir, yang tersisa hanyalah mengevaluasi matriks Hessian pada titik (1,1):

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

Latihan 2

Hitung Hessian di titik (1,1) fungsi dua variabel berikut:

$\displaystyle f(x,y)= e^{y\ln x}$

lihat solusi

Pertama, kita perlu menghitung turunan parsial orde pertama dari fungsi tersebut:

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

Setelah kita mendapatkan turunan pertama, kita menghitung turunan parsial orde kedua dari fungsi tersebut:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

Jadi matriks fungsi Hessian adalah matriks persegi berdimensi 2×2:

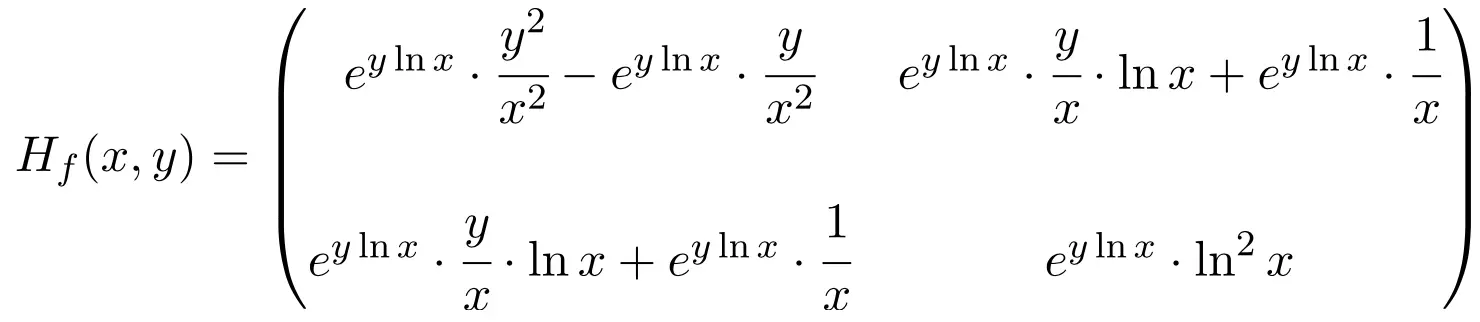
Latihan Hessian terpecahkan atau matriks Hessian berdimensi 2x2

Terakhir, yang tersisa hanyalah mengevaluasi matriks Hessian pada titik (1,1):

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Latihan 3

Temukan matriks Hessian pada titik tersebut

$(0,1,\pi)$

dari fungsi berikut dengan 3 variabel:

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

lihat solusi

Pertama, kita menghitung turunan parsial orde pertama dari fungsi tersebut:

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

Setelah kita mendapatkan turunan pertama, kita menghitung turunan parsial orde kedua dari fungsi tersebut:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

Sehingga matriks fungsi Hessian tersebut merupakan matriks persegi berdimensi 3×3:

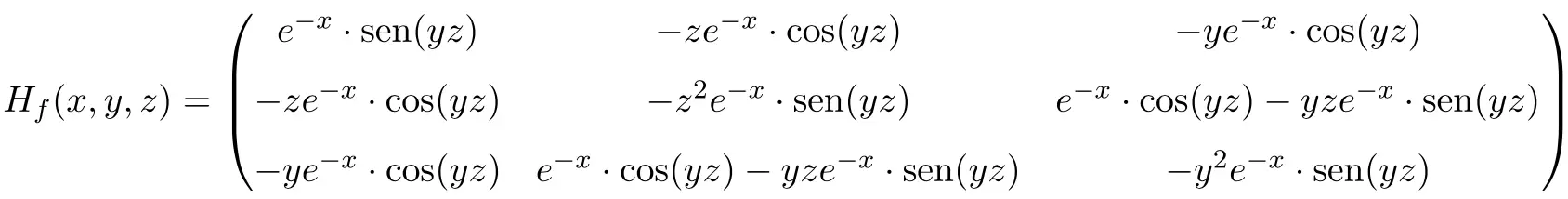
contoh matriks goni atau goni berdimensi 3x3

Terakhir, kita ganti variabel dengan nilainya masing-masing pada titik tersebut

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

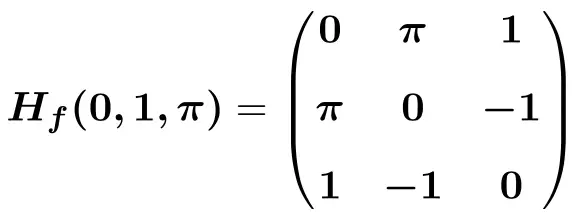
latihan diselesaikan selangkah demi selangkah dari matriks Hessian atau Hessian berdimensi 3x3

Latihan 4

Tentukan matriks Hessian di titik (2,-1,1,-1) fungsi berikut dengan 4 variabel:

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

lihat solusi

Langkah pertama adalah mencari turunan parsial orde pertama dari fungsi tersebut:

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

Sekarang kita selesaikan turunan parsial orde kedua dari fungsi tersebut:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

Jadi ekspresi matriks Hessian 4×4 yang diperoleh dengan menyelesaikan semua turunan parsialnya adalah sebagai berikut:

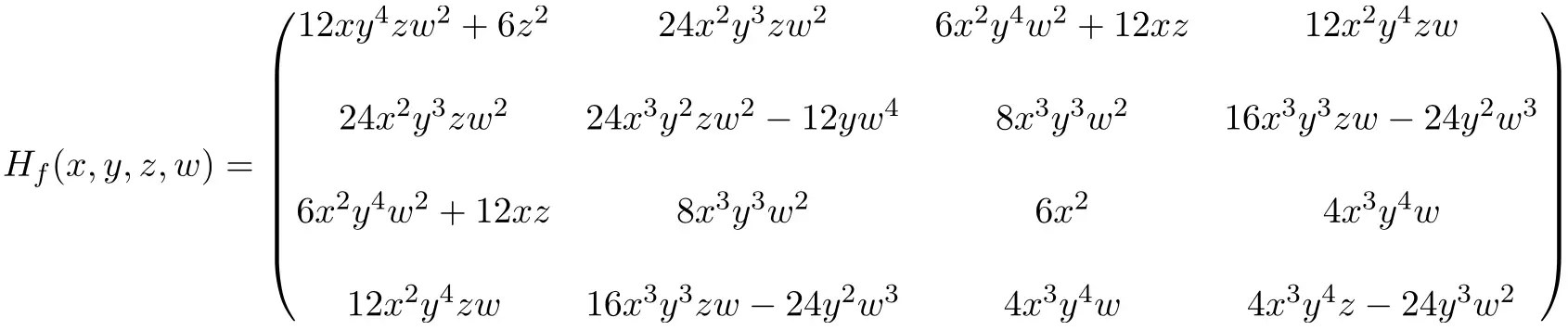
contoh diselesaikan langkah demi langkah goni atau matriks goni berdimensi 4x4

Terakhir, kami mengganti nilai titik masing-masing yang tidak diketahui (2,-1,1,-1) dan kami melakukan perhitungan:

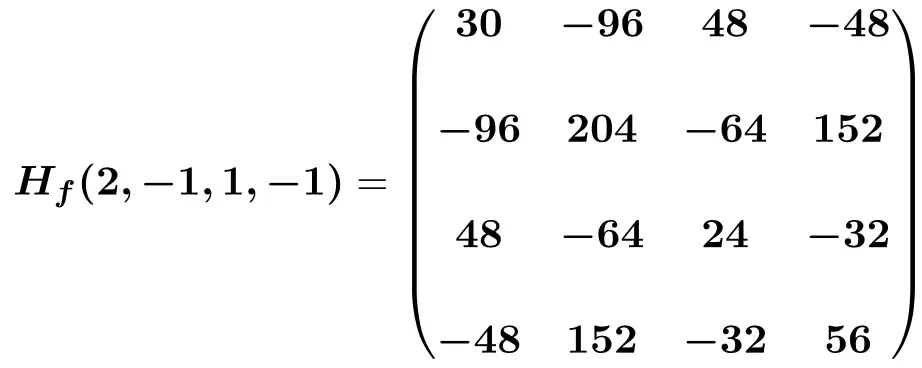
Latihan diselesaikan selangkah demi selangkah dari matriks Hessian atau Hessian berdimensi 4x4

Bagaimana cara mengetahui matriks Hessian positif, negatif, atau tak tentu?

Seperti yang akan kita lihat nanti, mengetahui apakah matriks Hessian merupakan matriks semi pasti positif, pasti positif, semi pasti negatif, pasti negatif, atau matriks tak tentu sangatlah berguna. Jadi mari kita lihat bagaimana kita bisa mengetahuinya:

Kriteria nilai eigen (atau nilai eigen)

Salah satu cara untuk mengetahui jenis matriksnya adalah dengan melihat nilai eigen (atau nilai eigen) dari matriks Hessian:

Matriks Hessian bersifat semi pasti positif jika mempunyai nilai eigen (atau nilai eigen) sama dengan dan lebih besar dari nol. Artinya, ia memiliki nilai eigen positif dan setidaknya satu sama dengan 0:

$\lambda \geq 0$

Matriks Hessian bersifat pasti positif jika semua nilai eigennya (atau nilai eigen) secara eksklusif lebih besar dari 0 (positif):

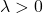$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul> <li> Matriks Hessian bersifat <span style=$ semi pasti negatif jika mempunyai nilai eigen (atau nilai eigen) sama dengan dan kurang dari nol. Artinya, ia memiliki nilai eigen negatif dan setidaknya satu sama dengan 0:

$\lambda \leq 0$

Matriks Hessian bersifat pasti negatif jika semua nilai eigennya (atau nilai eigennya) kurang dari 0 (negatif):

$\lambda < 0$

Matriks Hessian tidak terdefinisi jika memiliki nilai eigen (atau nilai eigen) positif dan negatif:

$\lambda > 0 \qquad \lambda <0$

Kriteria Sylvester

Cara lain untuk mengetahui jenis matriks Hessian adalah dengan menggunakan kriteria Sylvester, meskipun teorema ini hanya memberi tahu kita apakah matriks tersebut pasti positif, pasti negatif, atau tidak terbatas. Namun terkadang penggunaannya bisa jauh lebih cepat karena perhitungannya secara umum lebih mudah.

Jadi, kriteria Sylvester berbunyi sebagai berikut:

Jika semua minor utama matriks Hessian lebih besar dari 0, maka matriks tersebut termasuk matriks definit positif .

Jika minor utama matriks Hessian berindeks genap lebih besar dari 0 dan matriks berindeks ganjil kurang dari 0, maka matriks tersebut termasuk matriks definit negatif .

Jika semua minor utama matriks Hessian bukan 0 dan tidak satu pun dari dua kondisi sebelumnya terpenuhi, maka matriks tersebut merupakan matriks tak tentu .

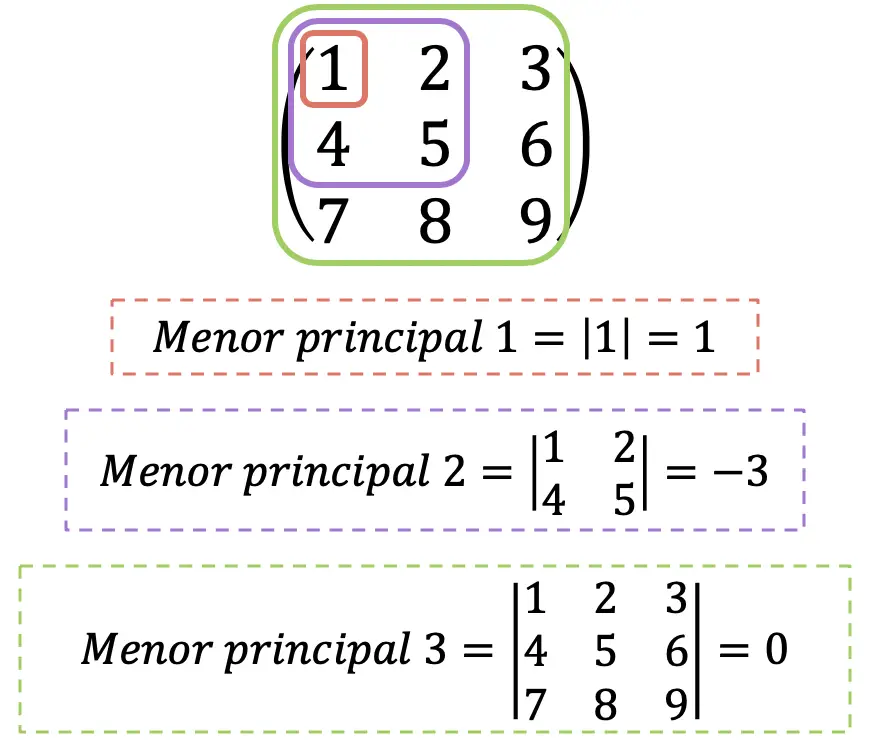
anak di bawah umur utama dari matriks Hessian

Jelasnya, minor utama maksimum matriks Hessian akan selalu berimpit dengan determinannya. Untuk tujuan informasi saja, determinan matriks Hessian disebut juga “Hessian”, meskipun kami tidak akan melakukannya di sini untuk menghindari kebingungan.

Cara menghitung maksimum atau minimum suatu fungsi dengan matriks Hessian

Setelah Anda mengetahui cara menghitung matriks Hessian, Anda mungkin bertanya-tanya: dan untuk apa matriks ini digunakan?

Nah, salah satu penerapan matriks Hessian adalah mencari maksimum atau minimum suatu fungsi dengan lebih dari satu variabel. Berikut penjelasan langkah demi langkah cara menghitung maksimum dan minimum:

Pertama, titik kritis dari fungsi multivariabel dihitung. Untuk melakukan ini, kita menghitung gradien atau matriks Jacobian dari fungsi tersebut, menetapkannya sama dengan 0 dan menyelesaikan persamaannya.
Matriks Hessian dihitung.
Titik kritis yang ditemukan pada langkah 1 disubstitusikan ke dalam matriks Hessian. Dengan demikian kita akan memperoleh matriks Hessian sebanyak titik kritis yang mempunyai fungsi.
Kita melihat jenis matriks apa yang dimiliki setiap matriks Hessian. Artinya, kita melihat apakah itu pasti positif, pasti negatif, tidak tentu, dll.
- Jika matriks Hessian berdefinisi positif, maka titik kritisnya adalah minimum relatif dari fungsi tersebut.
- Jika matriks Hessian pasti negatif, titik kritisnya adalah maksimum relatif dari fungsi tersebut.
- Jika matriks Hessian tidak terdefinisi, maka titik kritisnya adalah titik pelana .

Contoh penghitungan maksimum dan minimum suatu fungsi multivariabel

Untuk melihat cara melakukannya, berikut adalah contoh penghitungan dan klasifikasi ekstrem relatif suatu fungsi menggunakan matriks Hessian:

Temukan semua ekstrem relatif dari fungsi multivariabel berikut:

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

Hal pertama yang perlu kita lakukan adalah menghitung matriks Jacobian dari fungsi tersebut, yang dalam hal ini akan bertepatan dengan gradien karena merupakan fungsi skalar:

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

Sekarang kita harus menentukan titik kritisnya, untuk melakukan ini kita menyamakan persamaan yang diperoleh dengan 0 dan menyelesaikan sistem persamaan:

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

Jadi titik kritis yang kita temukan adalah (0,-2).

Setelah titik kritis fungsi ditemukan, kita harus menghitung matriks Hessian:

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Dan, tentu saja, matriks Hessian yang dievaluasi pada titik kritisnya adalah sama:

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Untuk melihat jenis matriksnya, kita akan menggunakan kriteria Sylvester. Oleh karena itu, kami menyelesaikan minor utama matriks:

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

Minor utama 1 (ganjil) adalah positif dan minor utama 2 (genap) negatif, jadi menurut kriteria Sylvester, matriks tersebut merupakan matriks tak tentu. Oleh karena itu, titik kritis (0,-2) merupakan titik pelana.

Menentukan kecekungan atau kecembungan suatu fungsi dengan matriks Hessian

Kegunaan lain dari matriks Hessian adalah untuk mengetahui apakah suatu fungsi cekung atau cembung. Dan hal ini dapat ditentukan berdasarkan teorema berikut:

Menjadi

$A \subseteq \mathbb{R}^n$

himpunan terbuka dan

$f \colon A \to \mathbb{R}$

suatu fungsi yang turunan keduanya kontinu, kecekungan dan kecembungannya ditentukan oleh matriks Hessian:

Fungsi
$f$

seluruhnya cembung

$A$

jika dan hanya jika matriks Hessiannya bersifat semi-pasti positif di setiap titik himpunan.
Fungsi
$f$

seluruhnya sangat cembung

$A$

jika dan hanya jika matriks Hessiannya berdefinisi positif di setiap titik himpunan.

✓ Oleh karena itu, jika

$f$

adalah fungsi cembung pada titik dimana matriks Jacobian juga hilang, titik ini merupakan minimum lokal .

Fungsi
$f$

secara keseluruhan cekung

$A$

jika dan hanya jika matriks Hessiannya bersifat semi-pasti negatif di setiap titik himpunan.
Fungsi
$f$

secara keseluruhan benar-benar cekung

$A$

jika dan hanya jika matriks Hessiannya berdefinisi negatif di setiap titik himpunan.

✓ Oleh karena itu, jika

$f$

adalah fungsi cekung pada suatu titik dimana matriks Jacobian juga hilang, titik ini merupakan maksimum lokal .

Di bawah ini Anda memiliki contoh fungsi cembung dan fungsi cekung lainnya yang direpresentasikan dalam ruang 3 dimensi:

fungsi cembung

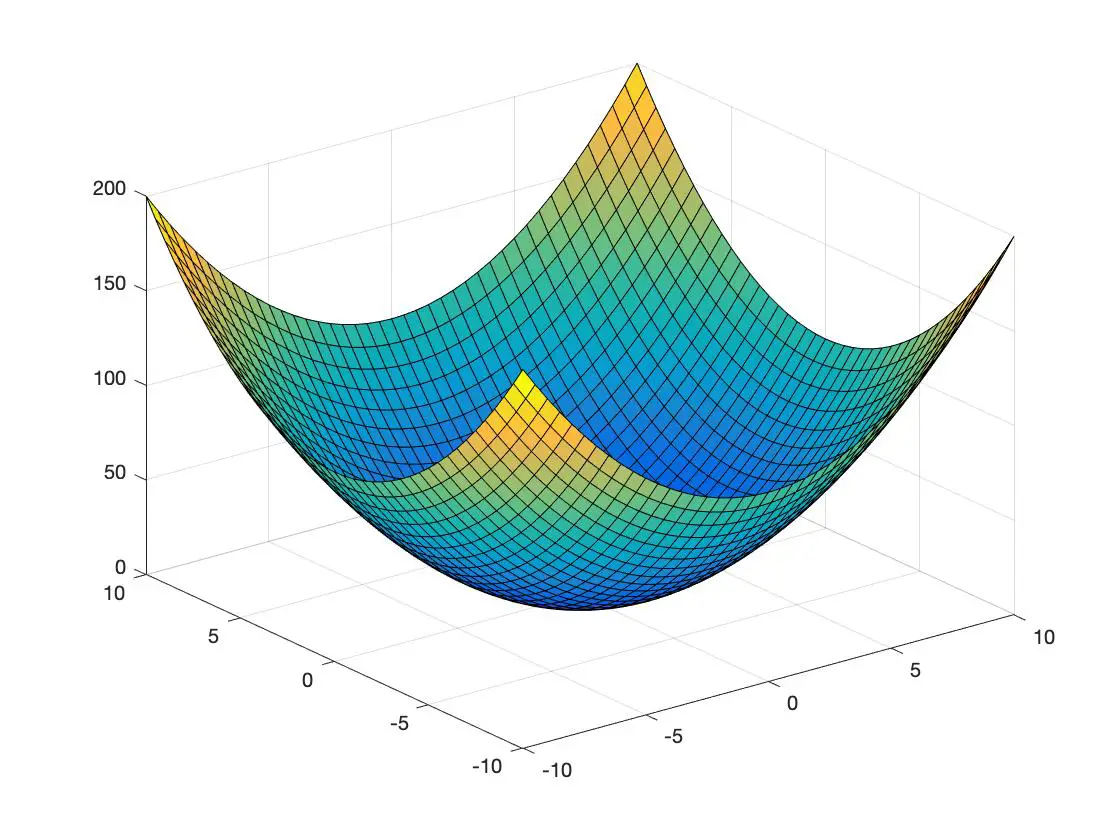
fungsi cekung

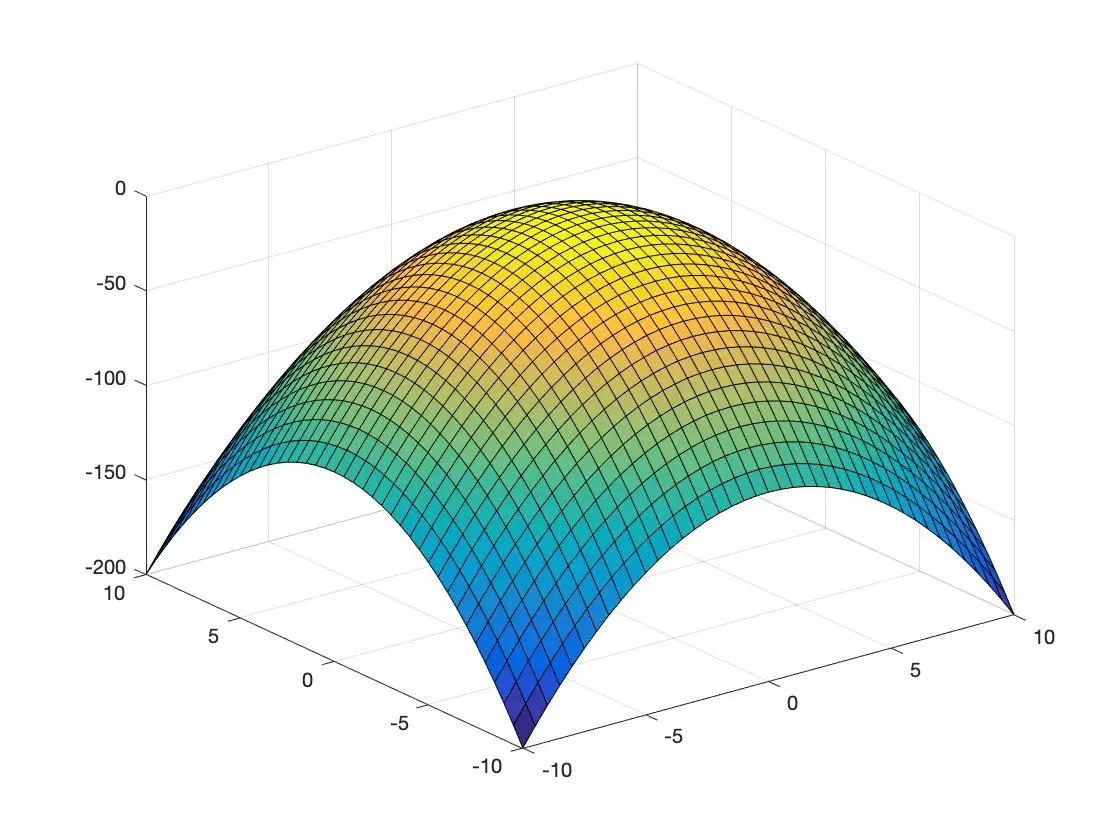
Gambar memiliki atribut ALT yang kosong; nama filenya adalah concavity-and-convexity-of-a-function-with-the-hessian-matrix-1024x768.jpg

Lebih banyak aplikasi matriks Hessian

Kegunaan utama matriks Hessian adalah yang telah kita lihat, namun ia juga memiliki penerapan lain. Kami menjelaskannya di bawah ini untuk yang paling penasaran.

Polinomial Taylor

Perluasan polinomial Taylor untuk fungsi 2 variabel atau lebih pada suatu titik

$a$

dimulai seperti ini:

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

Seperti yang Anda lihat, suku orde kedua dari pemuaian Taylor diberikan oleh matriks Hessian yang dievaluasi pada titik pemuaian polinomial.

Matriks Goni Berbatas

Kegunaan lain dari matriks Hessian adalah untuk menghitung minimum dan maksimum suatu fungsi multivariat

$f(x,y)$

dibatasi pada peran lain

$g(x,y)$

. Untuk mengatasi masalah ini, digunakan matriks Hessian berbatas dan prosedur berikut diikuti:

Langkah 1: Fungsi Lagrange dihitung, yang ditentukan oleh ekspresi berikut:

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

Langkah 2: Titik kritis fungsi Lagrange ditemukan. Untuk melakukan ini, kita menghitung gradien fungsi Lagrange, mengatur persamaan menjadi 0 dan menyelesaikan persamaan.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

Langkah 3: Untuk setiap titik yang kami temukan, kami menghitung batas Hessian, yang ditentukan oleh matriks berikut:

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

Langkah 4: Kami menentukan untuk setiap titik kritis apakah itu maksimum atau minimum:

Ini akan menjadi fungsi maksimum lokal
$f$

di bawah batasan fungsi

$g$

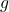
jika nm terakhir (di mana n adalah jumlah variabel dan m jumlah batasan) minor utama dari matriks Hessian berbatas yang dievaluasi pada titik kritis mempunyai tanda bolak-balik yang dimulai dengan tanda negatif.

Ini akan menjadi fungsi minimum lokal
$f$

di bawah batasan fungsi

$g$

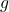
jika nm terakhir (di mana n adalah jumlah variabel dan m jumlah batasan) minor utama matriks Hessian tajam yang dievaluasi pada titik kritis semuanya mempunyai tanda negatif.

Perlu diingat bahwa nilai minimum dan maksimum relatif dari satu fungsi yang dibatasi dengan fungsi lainnya tidak harus sama untuk fungsi yang tidak dibatasi. Oleh karena itu, matriks Hessian berbatas hanya berguna untuk jenis masalah ini.

Hubungan dengan operasi lain

Terakhir, matriks Hessian juga dihubungkan dengan operasi atau matriks penting lainnya, terutama dengan matriks Jacobian dan dengan operator Laplace.

Hubungan dengan matriks Jacobian

Matriks Hessian suatu fungsi

$f$

adalah matriks Jacobian dari gradien fungsi yang sama:

$\displaystyle H_f = J(\nabla f)$

Operator Laplace

Jejak matriks Hessian setara dengan operator Laplace :

$\displaystyle tr( H_f) = \Delta f$

Kesetaraan ini dapat dibuktikan dengan mudah, karena definisi operator Laplace adalah divergensi gradien suatu fungsi:

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

Oleh karena itu ekspresinya adalah:

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

Dan jumlah ini hanyalah jejak matriks Hessian, sehingga kesetaraannya terbukti.

Matriks hessian (atau hesse)

Apa itu matriks Hessian?

Contoh penghitungan matriks Hessian

Memecahkan masalah matriks Hessian

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Bagaimana cara mengetahui matriks Hessian positif, negatif, atau tak tentu?

Kriteria nilai eigen (atau nilai eigen)

Kriteria Sylvester

Cara menghitung maksimum atau minimum suatu fungsi dengan matriks Hessian

Contoh penghitungan maksimum dan minimum suatu fungsi multivariabel

Menentukan kecekungan atau kecembungan suatu fungsi dengan matriks Hessian

Lebih banyak aplikasi matriks Hessian

Polinomial Taylor

Matriks Goni Berbatas

Hubungan dengan operasi lain

Hubungan dengan matriks Jacobian

Operator Laplace

Tinggalkan Komentar Batalkan Balasan