Matriks diagonal - Mathority

Pada halaman ini Anda akan melihat apa itu matriks diagonal dan contoh matriks diagonal. Selain itu, Anda akan mempelajari cara mengoperasikan matriks jenis ini, cara menghitung determinannya dengan mudah, dan cara membalikkannya. Ada juga sifat dan penerapan matriks diagonal. Dan terakhir, penjelasan tentang matriks bidiagonal dan matriks tridiagonal.

Apa itu matriks diagonal?

Matriks diagonal adalah matriks persegi yang semua elemen di luar diagonal utamanya bernilai nol (0). Elemen diagonal utama mungkin nol atau tidak.

Setelah kita mengetahui definisi pasti dari matriks diagonal, kita akan melihat contoh matriks diagonal:

Contoh matriks diagonal

Contoh matriks diagonal berdimensi 2×2

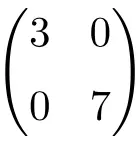
Contoh matriks diagonal berorde 3×3

Contoh matriks diagonal berukuran 4×4

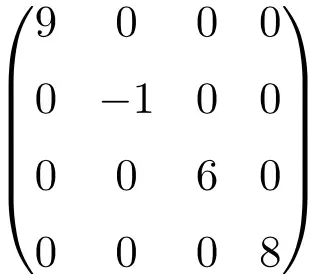
Matriks jenis ini umumnya ditulis dengan menunjukkan unsur-unsur diagonalnya:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Operasi dengan matriks diagonal

Salah satu alasan matriks diagonal sangat penting dalam aljabar linier adalah karena matriks tersebut memudahkan Anda dalam melakukan perhitungan. Inilah sebabnya mengapa mereka begitu digunakan dalam matematika.

Penjumlahan dan pengurangan matriks diagonal

Menjumlahkan (dan mengurangkan) dua matriks diagonal sangatlah sederhana: cukup tambahkan (atau kurangi) angka-angka pada diagonalnya.

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

Misalnya:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

Perkalian matriks diagonal

Untuk menyelesaikan perkalian atau hasil kali matriks dua matriks diagonal, cukup mengalikan elemen-elemen diagonalnya.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

Misalnya:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

Kekuatan matriks diagonal

Untuk menghitung pangkat matriks diagonal, kita perlu menaikkan setiap elemen diagonal menjadi eksponen:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

Misalnya:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

Penentu matriks diagonal

Penentu matriks diagonal adalah hasil kali elemen-elemen pada diagonal utama.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Lihatlah latihan penyelesaian berikut ini di mana kita mencari determinan matriks diagonal hanya dengan mengalikan elemen-elemen diagonal utamanya:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

Teorema ini mudah dibuktikan: Anda hanya perlu menghitung determinan matriks diagonal dengan blok (atau kofaktor). Demonstrasi ini dirinci di bawah ini menggunakan matriks diagonal umum:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

Membalikkan matriks diagonal

Suatu matriks diagonal dapat dibalik jika dan hanya jika semua elemen diagonal utama berbeda dari 0 . Dalam hal ini kita katakan bahwa matriks diagonalnya adalah matriks beraturan.

Selain itu, invers suatu matriks diagonal akan selalu berupa matriks diagonal lain dengan invers diagonal utama:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

Dari uraian sebelumnya, kita dapat menyimpulkan bahwa determinan invers suatu matriks diagonal adalah hasil kali invers diagonal utama:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

Sifat-sifat matriks diagonal

Setiap matriks diagonal juga merupakan matriks simetris .

Matriks diagonal adalah matriks yang berbentuk segitiga atas dan segitiga bawah .

Matriks identitasnya adalah matriks diagonal:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Demikian pula matriks nol juga merupakan matriks diagonal, karena semua elemennya yang tidak berada pada diagonalnya adalah nol. Meskipun angka pada diagonalnya adalah 0.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Nilai eigen (atau nilai eigen) suatu matriks diagonal adalah elemen-elemen diagonal utamanya.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

Suatu matriks persegi adalah diagonal jika dan hanya jika matriks tersebut berbentuk segitiga dan normal .

Adjoint suatu matriks diagonal adalah matriks diagonal lainnya.

Aplikasi Matriks Diagonal

Seperti yang telah kita lihat, menyelesaikan perhitungan dengan matriks diagonal sangat sederhana, karena banyak angka nol yang terlibat dalam operasinya. Oleh karena itu, mereka sangat berguna dalam bidang matematika dan digunakan secara luas.

Oleh karena itu, banyak penelitian telah dilakukan tentang cara mendiagonalisasi suatu matriks dan bahkan telah dikembangkan metode untuk mendiagonalisasi matriks (menggunakan polinomial karakteristik).

Oleh karena itu, matriks yang dapat didiagonalisasi juga cukup relevan. Seperti teorema dekomposisi spektral, yang menetapkan kondisi kapan suatu matriks dapat didiagonalisasi dan kapan tidak.

matriks bidiagonal

Matriks bidiagonal adalah matriks persegi yang semua elemennya yang tidak berada pada diagonal utama atau diagonal atas atau bawah bernilai 0.

Misalnya:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

matriks bidiagonal atas

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

matriks bidiagonal yang lebih rendah

Ketika diagonal utama dan superdiagonal pertama terisi, kita berbicara tentang matriks bidiagonal atas. Di sisi lain, ketika diagonal utama dan subdiagonal pertama terisi, kita berbicara tentang matriks bidiagonal yang lebih rendah.

matriks tridiagonal

Matriks tridiagonal adalah matriks persegi yang elemen-elemen bukan nolnya hanyalah diagonal utama dan diagonal-diagonal yang berdekatan di atas dan di bawahnya.

Misalnya:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

Jadi, semua matriks diagonal, bidiagonal, dan tridiagonal merupakan contoh matriks pita . Karena matriks pita adalah matriks yang semua elemen bukan nolnya mengelilingi diagonal utama.

Apa itu matriks diagonal?

Contoh matriks diagonal

Operasi dengan matriks diagonal

Penjumlahan dan pengurangan matriks diagonal

Perkalian matriks diagonal

Kekuatan matriks diagonal

Penentu matriks diagonal

Membalikkan matriks diagonal

Sifat-sifat matriks diagonal

Aplikasi Matriks Diagonal

matriks bidiagonal

matriks tridiagonal

Tinggalkan Komentar Batalkan Balasan