Matriks reguler - Mathority

Pada halaman ini Anda akan melihat apa itu matriks normal serta contoh matriks normal. Selain itu, Anda akan menemukan properti matriks jenis ini dan latihan yang diselesaikan langkah demi langkah.

Apa yang dimaksud dengan matriks normal?

Definisi array normal adalah:

Matriks normal adalah matriks kompleks yang dikalikan matriks transpos konjugasinya sama dengan hasil kali transpos konjugasinya dengan matriks itu sendiri.

$A\cdot A^*=A^*\cdot A$

Emas

$A^*$

adalah matriks transpos konjugat dari

$A$

Akan tetapi, jika matriks-matriks tersebut merupakan matriks bilangan riil , kondisi sebelumnya sama saja dengan mengatakan bahwa suatu matriks melakukan komutasi dengan transposnya, yaitu:

$A\cdot A^t=A^t\cdot A$

Karena, tentu saja, matriks transpos konjugasi dari matriks nyata hanyalah matriks transpos (atau transpos).

Contoh matriks normal

Contoh dengan bilangan kompleks

Matriks persegi kompleks berdimensi 2×2 berikut ini normal:

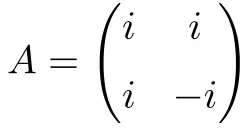
contoh matriks normal dengan bilangan kompleks berdimensi 2x2

Demonstrasi normalitasnya terlampir di bawah ini:

$\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

$\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

Contoh dengan bilangan real

Matriks persegi berikut dengan bilangan real berorde 2 juga normal:

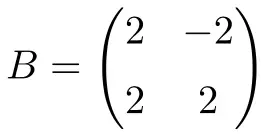
contoh matriks normal bilangan real berdimensi 2x2

Dalam hal ini, karena hanya mempunyai bilangan real, untuk membuktikan bahwa matriks tersebut normal cukup dengan memverifikasi bahwa matriks tersebut dapat diubah dengan transposnya:

$\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

$\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

Sifat-sifat matriks normal

Matriks normal mempunyai ciri-ciri sebagai berikut:

Semua matriks normal adalah matriks yang dapat didiagonalisasi.

Setiap matriks kesatuan juga merupakan matriks normal.

Demikian pula matriks Hermitian merupakan matriks normal.

Demikian pula matriks antihermitian merupakan matriks normal.

Jika A adalah matriks normal, maka nilai eigen (atau nilai eigen) matriks transpos konjugasi A* adalah nilai eigen konjugat dari A.

$\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i$

$\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i$

Dalam matriks normal, vektor eigen (atau vektor eigen) yang terkait dengan nilai eigen yang berbeda bersifat ortogonal.

Jika suatu matriks hanya terdiri dari bilangan real dan simetris , maka matriks tersebut sekaligus merupakan matriks normal.

Demikian pula matriks real antisimetris juga merupakan matriks normal.

Akhirnya, setiap matriks ortogonal yang dibentuk dari bilangan real juga merupakan matriks normal.

Latihan yang diselesaikan untuk matriks normal

Latihan 1

Pastikan matriks kompleks berdimensi 2 × 2 berikut ini normal:

$\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}$

lihat solusi

Untuk menunjukkan bahwa matriks tersebut normal terlebih dahulu kita harus menghitung transpos konjugasinya:

$\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}$

Dan sekarang kita melakukan verifikasi dengan mengalikan matriks A dengan matriks A* pada kedua kemungkinan arah:

$\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

Hasil perkalian kedua-duanya sama, sehingga matriks A normal.

Latihan 2

Tunjukkan bahwa matriks real berikut berukuran 2 × 2 adalah normal:

$\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}$

lihat solusi

Karena dalam kasus ini kita berurusan dengan lingkungan yang hanya berisi bilangan real, cukup dibuktikan bahwa hasil kali matriks antara matriks A dan transposnya memberikan hasil yang sama apa pun arah perkaliannya:

$\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

$\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

Hasil kedua perkaliannya sama, sehingga matriks A normal.

Latihan 3

Tentukan apakah matriks bilangan kompleks berorde 2 berikut ini normal:

$\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}$

lihat solusi

Untuk memeriksa apakah matriksnya normal, pertama-tama kita harus menghitung transpos konjugasinya:

$\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}$

Dan sekarang kita periksa apakah matriks A dan transpos konjugasinya dapat dialihkan:

$\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

Hasil perkalian kedua-duanya sama, sehingga matriks A normal.

Latihan 4

Pastikan matriks real berdimensi 3×3 berikut ini normal:

$\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}$

lihat solusi

Karena matriks seluruhnya terdiri dari unsur-unsur nyata, cukup dibuktikan bahwa hasil kali matriks antara matriks A dan transposnya tidak bergantung pada arah perkalian:

$\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

$\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

Hasil kedua perkaliannya sama, sehingga matriks A normal.

Latihan 5

Tentukan apakah matriks kompleks berorde 3×3 berikut ini normal:

$\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

lihat solusi

Pertama, kita menghitung transpos konjugasi matriks:

$\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

Sekarang kita perlu melakukan perkalian matriks antara matriks A dan transpos konjugasinya pada kedua arah yang memungkinkan. Namun matriks transpos konjugasi A sama dengan matriks A itu sendiri, sehingga merupakan matriks Hermitian. Oleh karena itu, dari sifat-sifat matriks normal maka A adalah matriks normal , karena setiap matriks Hermitian adalah matriks normal.

Matriks biasa

Apa yang dimaksud dengan matriks normal?

Contoh matriks normal

Contoh dengan bilangan kompleks

Contoh dengan bilangan real

Sifat-sifat matriks normal

Latihan yang diselesaikan untuk matriks normal

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan