Di halaman ini Anda akan melihat apa itu matriks antihermitian, disebut juga matriks antihermitian. Anda akan menemukan contoh matriks anti-Hermitian, semua propertinya, dan bentuk matriks persegi kompleks jenis ini. Terakhir, Anda akan menemukan penjelasan tentang cara menguraikan matriks kompleks apa pun menjadi jumlah matriks anti-Hermitian ditambah matriks Hermitian lainnya.
Apa yang dimaksud dengan matriks antihermitian atau antihermitian?
Matriks anti-Hermitian , atau disebut juga matriks anti-Hermitian, adalah matriks persegi dengan bilangan kompleks yang transpos konjugasinya sama dengan matriks yang sama tetapi bertanda berbeda.
![]()
Emas
![]()
adalah matriks konjugasi yang ditransposisikan dari
![]()
.
Karena penasaran, matriks jenis ini dinamakan demikian karena memenuhi kondisi kebalikan dari matriks Hermitian , yang namanya berasal dari matematikawan penting Perancis Charles Hermite, seorang profesor dan peneliti matematika abad ke-19 yang melakukan penelitian penting termasuk di bidang aljabar linier.
Contoh matriks antihermitian
Setelah kita melihat definisi matriks antihermitian (atau matriks antihermitian), kita akan melihat beberapa contoh matriks antihermitian dengan dimensi berbeda:
Contoh matriks anti-Hermitian berorde 2×2
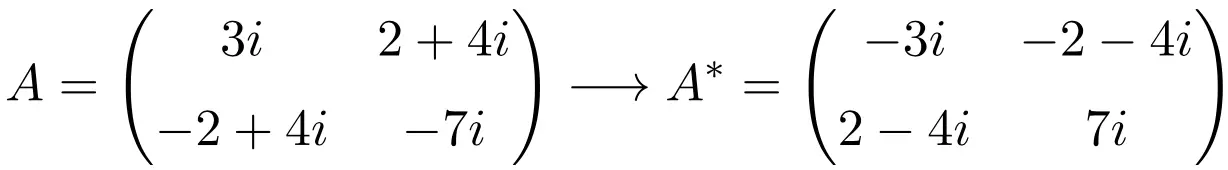
Contoh matriks antihermitian berdimensi 3×3
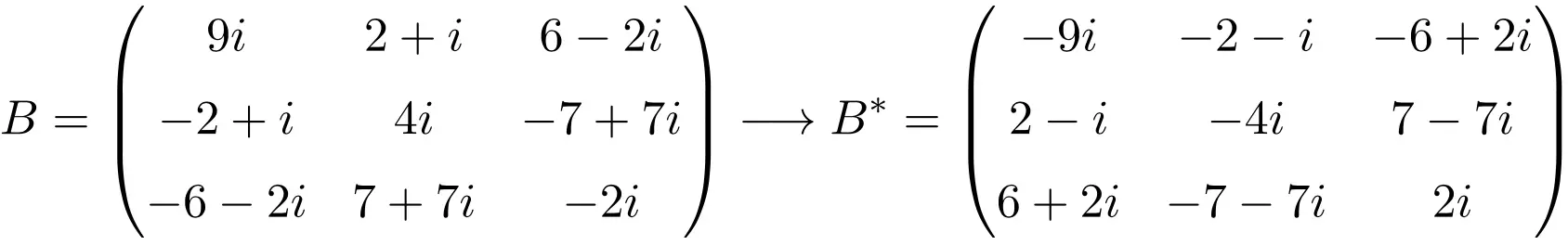
Contoh matriks anti hermitian berukuran 4×4
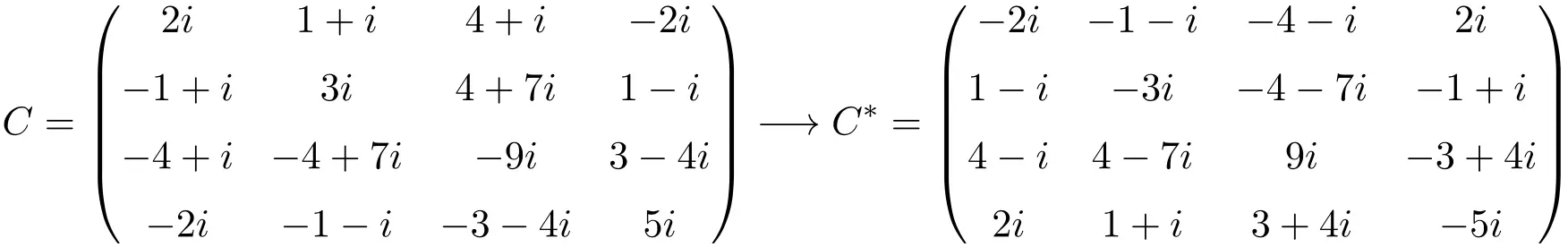
Seperti yang Anda lihat, matriks A, B, dan C adalah anti-Hermitian karena matriks transpos konjugasi masing-masing matriks sama dengan matriks itu sendiri tetapi semua elemennya berubah tanda.
Struktur matriks antihermitian
Jika Anda telah melihat contoh sebelumnya, matriks anti-Hermitian selalu memiliki struktur yang sama: matriks tersebut terdiri dari bilangan imajiner (tanpa bagian real) pada diagonal utama, dan elemen kompleks yang terletak pada garis ke-i dan garis ke-j. garis. kolom harus mempunyai bagian imajiner yang sama dan bagian nyata yang sama tetapi berubah tanda sebagai elemen baris ke-j dan kolom ke-i.
Meskipun ini mungkin tampak agak rumit, namun pastinya lebih baik dipahami dengan contoh berikut:
Struktur matriks antihermitian berdimensi 2×2
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f160fc8949e4256fcf771e7be11c517_l3.png)
Seperti yang Anda lihat, elemen-elemen diagonal utama matriks anti-Hermitian sepenuhnya imajiner dan elemen-elemen diagonal sekunder memiliki bagian imajiner yang sama dan bagian nyata telah berubah tanda.
Oleh karena itu, bagian nyata matriks anti-Hermitian harus antisimetris dan bagian imajinernya simetris.
Sifat-sifat matriks antihermitian
Sekarang kita akan melihat apa saja sifat-sifat matriks kompleks persegi jenis ini:
- Setiap matriks antihermitian merupakan contoh matriks normal . Meskipun tidak semua matriks normal merupakan matriks antihermitik.
- Matriks anti-Hermitian apa pun dapat didiagonalisasi. Selanjutnya, matriks diagonal yang dihasilkan hanya mengandung elemen imajiner murni.
- Oleh karena itu, nilai eigen (atau nilai eigen) dari matriks anti-Hermitian selalu berupa bilangan imajiner.
- Demikian pula, vektor eigen (atau vektor eigen) dari nilai eigen yang berbeda dari matriks anti-Hermitian adalah ortogonal.
- Suatu matriks bilangan real, artinya tidak ada unsur yang mempunyai bagian imajiner, adalah anti-Hermitian jika dan hanya jika matriks tersebut merupakan matriks antisimetris .
- Matriks anti-Hermitian dapat dinyatakan sebagai jumlah matriks antisimetri nyata dan matriks simetri imajiner.
![]()
- Jumlah (atau pengurangan) dua matriks anti-Hermitian sama dengan matriks anti-Hermitian lainnya.
- Hasil perkalian matriks anti-Hermitian dan skalar adalah matriks anti-Hermitian lainnya jika skalarnya adalah bilangan real.
- Pangkat matriks anti-Hermitian sama dengan matriks anti-Hermitian jika eksponennya ganjil; sebaliknya jika dipangkatkan menjadi eksponen genap maka hasilnya adalah matriks Hermitian.
- Ya

adalah matriks antihermitian, maka produknya
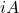
adalah matriks Hermitian.
Penguraian matriks kompleks menjadi matriks anti-Hermitian dan matriks Hermitian
Matriks apa pun yang mengandung bilangan kompleks dapat diuraikan menjadi jumlah matriks anti-Hermitian ditambah matriks Hermitian lainnya . Namun untuk ini Anda perlu mengetahui ciri-ciri dari jenis matriks berikut ini:
- Jumlah matriks kompleks persegi ditambah konjugat transposnya setara dengan matriks Hermitian (atau Hermitian):
![]()
- Selisih antara matriks kompleks persegi dan konjugatnya yang ditransposisikan sama dengan matriks anti-Hermitian:
![]()
- Oleh karena itu, semua matriks kompleks dapat diuraikan menjadi jumlah matriks Hermitian dan matriks anti-Hermitian. Teorema ini dikenal sebagai dekomposisi Teoplitz :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74e1d9a0d55d77dd927109e42986c200_l3.png)
Dimana C adalah matriks kompleks yang ingin kita dekomposisi, C* adalah konjugat yang ditransposisikan, dan terakhir A dan B masing-masing adalah matriks Hermitian dan anti-Hermitian yang menjadi tempat dekomposisi matriks C.