Masalah optimasi -

Di sini kami menjelaskan bagaimana masalah optimasi fungsi diselesaikan secara bertahap. Selain itu, Anda akan dapat berlatih dengan latihan yang diselesaikan pada masalah optimasi.

Apa masalah optimasi?

Masalah optimasi adalah masalah dimana seseorang harus mencari maksimum atau minimum suatu fungsi. Misalnya, masalah optimasi akan melibatkan penghitungan fungsi maksimum yang menentukan keuntungan perusahaan.

Bagaimana mengatasi masalah optimasi

Langkah-langkah untuk mengatasi masalah pengoptimalan fungsi:

Atur fungsi yang perlu dioptimalkan.
Turunkan fungsi yang akan dioptimalkan.
Temukan titik kritis dari fungsi yang akan dioptimalkan. Untuk melakukan ini, Anda perlu mengatur turunan fungsi sama dengan nol dan menyelesaikan persamaan yang dihasilkan.
Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Contoh masalah optimasi

Dengan mempertimbangkan teori masalah optimasi, kita akan menyelesaikan masalah jenis ini langkah demi langkah sehingga Anda dapat melihat cara penyelesaiannya.

Diantara semua segitiga siku-siku yang panjang kaki-kakinya 10 cm, hitunglah luas segitiga yang luas permukaannya maksimum.

Untuk menyelesaikan soal ini, kita akan memanggil salah satu cabang segitiga x , dan cabang lainnya y :

Langkah 1: Atur fungsi yang akan dioptimalkan.

Kita ingin luas segitiganya maksimal, dan rumus luas segitiga adalah:

$A = \cfrac{b \cdot h}{2}$

Dalam kasus kita, alas segitiga adalah x dan tingginya adalah y . Belum:

$A = \cfrac{x \cdot y}{2}$

Kita sudah mempunyai fungsi untuk mengoptimalkannya, namun bergantung pada dua variabel sedangkan hanya dapat bergantung pada satu variabel. Namun, pernyataan tersebut memberitahu kita bahwa kedua kakinya harus berjumlah 10 cm. Belum:

$x+ y = 10$

Kami menyelesaikan y dari persamaan ini:

$y = 10 -x$

Dan kami mengganti ekspresi tersebut ke dalam fungsi:

$A = \cfrac{x \cdot y}{2} \ \xrightarrow{ y \ = \ 10 -x } \ A = \cfrac{x(10-x)}{2}$

$A(x) = \cfrac{10x-x^2}{2}$

Kita sekarang memiliki fungsi optimasi terencana dan itu hanya bergantung pada satu variabel, jadi kita bisa melanjutkan ke langkah berikutnya.

Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

Ini adalah fungsi rasional, jadi kami menerapkan rumus turunan pembagian untuk menurunkannya:

$A(x) = \cfrac{10x-x^2}{2} \ \longrightarrow \ A'(x) = \cfrac{(10-2x) \cdot 2 - (10x-x^2) \cdot 0}{2^2}$

$A'(x) = \cfrac{20-4x}{4}$

Langkah 3: Temukan titik kritisnya.

Untuk menemukan titik kritis suatu fungsi, kita perlu mengatur turunannya sama dengan nol dan menyelesaikan persamaan yang dihasilkan:

$A'(x) = 0$

$\cfrac{20-4x}{4} =0$

Angka 4 membagi seluruh ruas kiri, sehingga kita dapat mengalikannya dengan mengalikan seluruh ruas kanan:

$20-4x=0 \cdot 4$

$20-4x=0$

$-4x=-20$

$x=\cfrac{-20}{-4}$

$x=5$

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Untuk mempelajari kemonotonan suatu fungsi, kita nyatakan titik kritis di sebelah kanan:

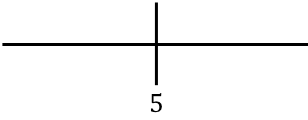
Dan sekarang kita evaluasi tanda turunannya pada setiap interval untuk mengetahui apakah fungsinya naik atau turun. Untuk melakukan ini, kita mengambil sebuah titik di setiap interval (bukan titik kritisnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:

$A'(x) = \cfrac{20-4x}{4}$

$A'(0) = \cfrac{20-4\cdot0}{4} = \cfrac{20}{4} = 5 \ \rightarrow \ \bm{+}$

$A'(6) = \cfrac{20-4\cdot6}{4} = \cfrac{20-24}{4} = \cfrac{-4}{4} = -1 \ \rightarrow \ \bm{-}$

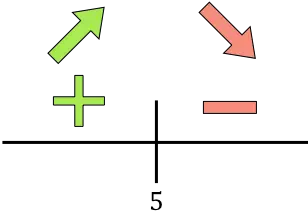
Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval kenaikan dan penurunan fungsi tersebut adalah:

Pertumbuhan:

$\bm{(-\infty, 5)}$

Mengurangi:

$\bm{(5,+\infty)}$

Pada x=5 fungsinya berubah dari naik ke turun, jadi x=5 adalah maksimum relatif dari fungsi yang akan dioptimalkan .

Jadi x=5 adalah nilai cabang segitiga yang mempunyai luas maksimum. Cukup hitung nilai kaki lainnya:

$y = 10 -x \ \xrightarrow{x \ = \ 5} \ y = 10-5= \bm{5}$

Kesimpulannya, nilai maksimal luas maksimum segitiga adalah:

$\bm{x=5} \ \mathbf{cm}$

$\bm{y=5} \ \mathbf{cm}$

Masalah optimasi teratasi

Masalah 1

Obatnya diberikan kepada orang sakit dan

$t$

beberapa jam kemudian, konsentrasi bahan aktif dalam darah ditentukan oleh fungsinya

$c(t) = te^{−t/2}$

miligram per mililiter. Tentukan nilai maksimum dari

$c(t)$

dan menunjukkan kapan nilai tersebut tercapai.

Lihat solusinya

Langkah 1: Atur fungsi yang akan dioptimalkan.

Dalam soal ini, mereka sudah memberi kita fungsi yang diusulkan, yaitu

$\displaystyle c(t) = t e^{-t/2} .$

Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

Fungsi tersebut terdiri dari hasil kali 2 fungsi. Oleh karena itu, untuk menghitung turunan suatu fungsi, kita harus menerapkan aturan turunan suatu produk:

$\displaystyle c'(t)=1 \cdot e^{-t/2} + t \cdot e^{-t/2} \cdot \left( \frac{-t}{2} \right)'= e^{-t/2} + t e^{-t/2} \cdot \frac{-1}{2}$

$c'(t)=e^{-t/2} + \cfrac{-1}{2}t e^{-t/2}$

Langkah 3: Temukan titik kritisnya.

Untuk menemukan titik kritis dari fungsi tersebut, kita menyelesaikannya

$c'(t)=0:$

$c'(t)=0$

$\displaystyle e^{-t/2} + \frac{-1}{2}t e^{-t/2}=0$

Kami mengambil faktor persekutuan untuk menyelesaikan persamaan:

$\displaystyle e^{-t/2} \left(1 - \frac{1}{2}t \right) = 0$

Agar perkaliannya sama dengan 0, salah satu dari dua unsur perkaliannya harus nol. Oleh karena itu, kami menetapkan setiap faktor sama dengan 0:

$\displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}$

Suatu bilangan yang dipangkatkan ke bilangan lain tidak akan pernah menghasilkan 0, oleh karena itu,

$e^{-t/2}=0$

Tidak ada solusi.

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Untuk mempelajari kemonotonan suatu fungsi, kita nyatakan titik kritis di sebelah kanan:

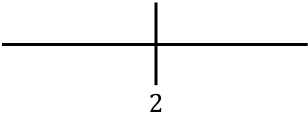
Dan sekarang kita evaluasi tanda turunannya pada setiap interval, untuk mengetahui apakah fungsinya naik atau turun. Oleh karena itu, kita mengambil sebuah titik di setiap interval (bukan titik kritisnya) dan melihat tanda apa yang dimiliki turunannya pada titik tersebut:

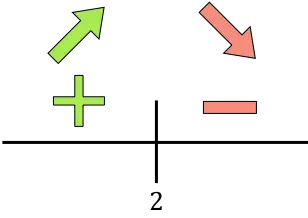
$\displaystyle c'(0)=e^{-0/2} + \frac{-1}{2}\cdot 0 \cdot e^{-0/2} = e^0 +\frac{-1}{2}\cdot 0 \cdot e^{0} = 1 + 0 = 1 \ \rightarrow \ \bm{+}$

$\displaystyle c'(3)=e^{-3/2} + \frac{-1}{2}(3)e^{-3/2} = 0,22-0,33 = -0,11 \ \rightarrow \ \bm{-}$

Jika turunannya positif berarti fungsinya bertambah, sebaliknya jika turunannya negatif berarti fungsinya menurun. Dengan demikian interval pertumbuhan dan penurunan fungsi yang akan dioptimalkan adalah:

Pertumbuhan:

$\bm{(-\infty,2)}$

Mengurangi:

$\bm{(2,+\infty)}$

Fungsi tersebut berubah dari naik ke turun pada t=2, jadi t=2 adalah maksimum dari fungsi tersebut. Oleh karena itu, konsentrasi maksimum akan tercapai dalam t=2 jam.

Terakhir, kita substitusikan nilai terjadinya maksimum ke dalam fungsi aslinya, untuk mencari nilai konsentrasi maksimum:

$c(2) = 2 \cdot e^{-2/2} = 2\cdot e^{-1} = 2 \cdot 0,37 = \bm{0,74} \ \mathbf{mg/ml}$

Masalah 2

Sebuah toko berharap dapat menjual 40 skuter listrik dengan harga €1.000 per skuter. Namun menurut riset pasar, untuk setiap penurunan harga skuter sebesar €50, akan terjadi peningkatan penjualan 10 skuter terlaris.

Pertama, tuliskan fungsi pendapatan toko berdasarkan berapa kali harga awal skuter sebesar $1.000 dikurangi sebesar $50. Selanjutnya menentukan harga skutik tersebut untuk mendapatkan keuntungan maksimal dan pendapatan yang diperoleh pada harga tersebut.

Lihat solusinya

Langkah 1: Atur fungsi yang akan dioptimalkan.

Pernyataan masalah memberi kita petunjuk, karena menyatakan bahwa fungsi tersebut harus bergantung pada berapa kali harga awal dikurangi sebesar $50. Oleh karena itu kita akan menyebutkan x berapa kali harga diturunkan sebesar €50:

$x= \text{N\'umero de veces que se rebaja el precio 50}$

€

Fungsi pendapatan adalah jumlah skuter yang terjual dikalikan harga tiap skuter:

$I(x)= \text{N\'umero patintetes vendidos} \cdot \text{Precio de cada patinete}$

Jumlah skuter yang terjual akan menjadi 40 ditambah 10 skuter untuk setiap pengurangan harga €50. Belum:

$\text{N\'umero patintetes vendidos} = 40 + 10x$

Harga setiap skuter akan menjadi €1000 pada awalnya, dan akan turun sebesar €50 dengan setiap penurunan harga. Belum:

$\text{Precio de cada patinete} = 1000 -50x$

Oleh karena itu, fungsi untuk mengoptimalkan masalah adalah:

$I(x)= \text{N\'umero patintetes vendidos} \cdot \text{Precio de cada patinete}$

$I(x)= (40 + 10x) \cdot (1000-50x)$

$I(x)= 40000-2000x+10000x-500x^2$

$I(x)= -500x^2+8000x+40000$

Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

Karena fungsi polinomial, turunannya lebih mudah dihitung:

$I(x)= -500x^2+8000x+40000\ \longrightarrow \ I'(x)= -1000x+8000$

Langkah 3: Temukan titik kritis dari fungsi tersebut.

Untuk menemukan titik kritis dari fungsi tersebut, kita menyelesaikannya

$I'(x)=0:$

$I'(x)=0$

$-1000x+8000=0$

$-1000x=-8000$

$x=\cfrac{-8000}{-1000} = 8$

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Untuk mempelajari monotonisitas suatu fungsi, kami mewakili titik kritis yang dihitung pada garis bilangan:

$I'(0)= -1000\cdot 0+8000=8000 \ \rightarrow \ \bm{+}$

$I'(10)= -1000\cdot 10+8000=-2000 \ \rightarrow \ \bm{-}$

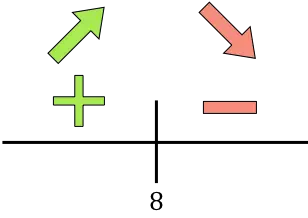
Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:

Pertumbuhan:

$\bm{(-\infty,8)}$

Mengurangi:

$\bm{(8,+\infty)}$

Fungsi tersebut berubah dari naik ke turun pada x=8, jadi x=8 adalah maksimum dari fungsi tersebut. Oleh karena itu, pendapatan maksimum akan diperoleh dengan melakukan pengurangan €50 sebanyak 8 kali.

Sekarang kita substitusikan nilai dimana pendapatan maksimum muncul ke dalam fungsi aslinya, untuk mencari nilai pendapatan maksimum:

$I(x)= -500x^2+8000x+40000$

$I(8)= -500\cdot 8^2+8000\cdot 8+40000 = \bm{72000}$

€

Dan harga setiap skuter setelah melakukan diskon €50 sebanyak 8 kali adalah:

$\text{Precio de cada patinete} = 1000 -50x$

$\text{Precio de cada patinete} = 1000 -50\cdot 8=\bm{600}$

€

Masalah 3

Fungsi biaya (dalam ribuan euro) suatu perusahaan dapat ditentukan dengan menggunakan ekspresi berikut:

$f(x)=40-6x+x^2, \quad x \ge 0$

Emas

$x$

mewakili ribuan unit yang diproduksi dari suatu barang tertentu.

Tentukan berapa banyak yang harus diproduksi agar biayanya minimal, berapa biayanya, dan berapa biayanya jika barang-barang tersebut tidak diproduksi.

Lihat solusinya

Langkah 1: Atur fungsi yang akan dioptimalkan.

Pernyataan masalah sudah memberi kita fungsi yang akan dioptimalkan, yaitu

$\displaystyle f(x)=40-6x+x^2 .$

Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

$f(x)=40-6x+x^2 \ \longrightarrow \ f'(x)=-6+2x$

Langkah 3: Temukan titik kritisnya.

Untuk menemukan titik kritis dari fungsi tersebut, kita menyelesaikannya

$f'(x)=0:$

$f'(x)=0$

$-6+2x=0$

$2x=6$

$x=\cfrac{6}{2} = 3$

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Kami mewakili titik kritis yang ditemukan di sebelah kanan:

$f'(0)=-6+2\cdot 0=-6\ \rightarrow \ \bm{-}$

$f'(4)=-6+2\cdot 4=-6+8=2\ \rightarrow \ \bm{+}$

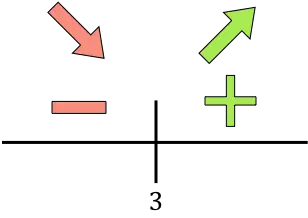
Jika turunannya lebih besar dari nol, maka fungsinya meningkat pada interval ini. Sebaliknya, jika turunannya kurang dari nol, maka fungsi tersebut menurun pada interval tersebut. Jadi, interval kenaikan dan penurunan fungsi tersebut adalah:

Pertumbuhan:

$\bm{(3,+\infty)}$

Mengurangi:

$\bm{(-\infty,3)}$

Fungsi tersebut berubah dari menurun menjadi meningkat pada x=3, jadi x=3 adalah fungsi minimum . Oleh karena itu, biaya minimum akan dicapai dengan memproduksi 3.000 unit.

Sekarang kita substitusikan nilai dimana biaya minimum tercapai ke dalam fungsi asli untuk mencari nilai biaya minimum:

$f(3)=40-6\cdot 3+3^2=\bm{31}$

jutaan euro.

Di sisi lain, mereka bertanya kepada kami berapa biayanya jika tidak ada produksi, yaitu kapan

$x= 0 .$

Oleh karena itu perlu dilakukan perhitungan

$f(0):$

$f(0)=40-6\cdot 0+0^2= \bm{40}$

jutaan euro.

Masalah 4

Kita ingin membuat rangka kayu berbentuk persegi panjang yang membatasi luas 2 m ² . Kita tahu bahwa harga kayu adalah €7,5/m untuk sisi horizontal dan €12,5/m untuk sisi vertikal. Tentukan dimensi yang harus dimiliki persegi panjang tersebut sehingga total biaya rangka adalah seminimal mungkin dan biaya tersebut minimum.

Lihat solusinya

Langkah 1: Atur fungsi yang akan dioptimalkan.

Untuk menyelesaikan soal ini, kita beri nama sisi horizontal x , dan sisi vertikal y :

Membeli sisi horizontal berharga €7,5 dan membeli sisi vertikal berharga €12,5. Selain itu, untuk setiap frame kita memerlukan dua sisi horizontal dan dua sisi vertikal. Oleh karena itu, biaya rangka dapat ditentukan dengan fungsi berikut:

$C(x,y)= 7,5\cdot 2x+12,5 \cdot 2y = 15x +25y$

Kami sudah memiliki fungsi untuk mengoptimalkan. Tapi itu bergantung pada dua variabel, padahal hanya bisa bergantung pada satu variabel. Namun pernyataan tersebut memberitahu kita bahwa luas permukaan bingkai harus 2 m ² . Belum:

$x \cdot y = 2$

Kami menghapus variabel y :

$y =\cfrac{2}{x}$

Dan kami mengganti ekspresi yang ditemukan dalam fungsi yang akan dioptimalkan:

$C(x,y)= 15x +25y\ \xrightarrow{y \ = \ \frac{2}{x} } \ C(x)= 15x+25\left(\cfrac{2}{x} \right)$

$C(x)= 15x+\cfrac{50}{x} =15x +50x^{-1}$

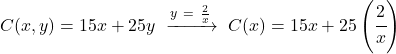
Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

$C(x)=15x +50x^{-1} \ \longrightarrow \ C'(x)=15 -50x^{-2}$

Langkah 3: Temukan titik kritisnya.

Untuk menemukan titik kritis dari fungsi tersebut, kita menyelesaikannya

$C'(x)=0:$

$C'(x)=0$

$15 -50x^{-2}=0$

$15 =50x^{-2}$

$15=\cfrac{50}{x^2}$

$\cfrac{15}{1}=\cfrac{50}{x^2}$

Kami mengalikan secara melintang untuk menyelesaikan persamaan dengan pecahan:

$15 \cdot x^2 = 50 \cdot 1$

$x^2 = \cfrac{50}{15}$

$x^2 = 3,33$

$\sqrt{x^2} = \sqrt{3,33}$

$x = 1,83$

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Kami mewakili titik kritis yang ditemukan untuk menganalisis fungsi monoton pada garis:

$f'(1)=15 -50\cdot 1^{-2} = 15-50 = -35 \ \rightarrow \ \bm{-}$

$f'(2)=15 -50\cdot 2^{-2} = 15-12,5 = 2,5 \ \rightarrow \ \bm{+}$

Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:

Pertumbuhan:

$\bm{(1,83,+\infty)}$

Mengurangi:

$\bm{(-\infty,1,83)}$

Fungsinya berubah dari turun ke naik pada x=1,83, jadi x=1,83 adalah fungsi minimum .

Oleh karena itu, x=1,83 adalah nilai sisi horizontal yang mewakili biaya minimum. Sekarang mari kita hitung nilai sisi vertikalnya:

$y =\cfrac{2}{x} \ \longrightarrow \ y =\cfrac{2}{1,83} = \bm{1,09}$

Dengan demikian, nilai-nilai yang membentuk biaya kerangka minimum adalah:

sisi horisontal

$= x = \bm{1,83} \ \mathbf{m}$

sisi vertikal

$= y = \bm{1,09} \ \mathbf{m}$

Dan biaya minimum yang dicapai dengan nilai tersebut adalah:

$C= 15\cdot 1,83+25\cdot 1,09=\bm{54,70}$

€

Masalah 5

Pintu katedral dibentuk oleh lengkungan setengah lingkaran yang ditopang oleh dua kolom, seperti terlihat pada gambar berikut:

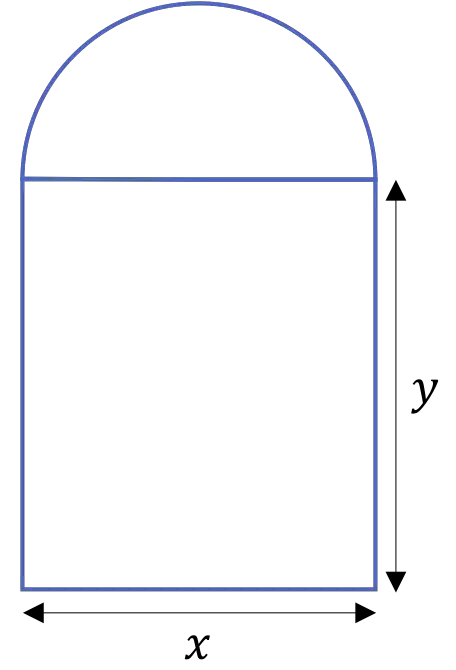
Jika keliling pintu adalah 20 m, tentukanlah pengukurannya

$x$

Dan

$y$

yang memaksimalkan luas permukaan seluruh pintu.

Lihat solusinya

Langkah 1: Atur fungsi yang akan dioptimalkan.

Luas lingkaran dihitung dengan rumus

$\pi r^2.$

Jadi luas seluruh pintu adalah luas persegi panjang ditambah setengah luas kelilingnya:

$A(x,y)= x\cdot y + \cfrac{1}{2} \left[ \pi r ^2 \right]$

$A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]$

$A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]$

$A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]$

$A(x,y)= xy +\cfrac{\pi x^2}{8}$

Kami sudah memiliki fungsi untuk mengoptimalkan. Tapi itu bergantung pada dua variabel, padahal hanya bisa bergantung pada satu variabel.

Namun, rilis tersebut memberitahu kita bahwa keliling seluruh gerbang adalah 20m. Keliling lingkaran dihitung dengan rumus

$2 \pi r.$

Oleh karena itu, keliling seluruh pintu adalah:

$P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }$

Kelilingnya harus 20 m. Oleh karena itu, kami menetapkan ekspresi sebelumnya sama dengan 20 untuk menemukan hubungan antara keduanya

$x$

Dan

$y :$

$x+2y + \cfrac{ \pi x }{2 } = 20$

Kami mengalikan semua suku dengan 2 untuk menghilangkan pecahan:

$2\cdot x+2\cdot 2y + 2 \cdot \cfrac{ \pi x }{2 } = 2 \cdot 20$

$2x+4y + \pi x = 40$

Kami membersihkan

$y :$

$4y = 40-2x- \pi x$

$y = \cfrac{40-2x- \pi x}{4}$

Dan kami mengganti ekspresi yang ditemukan dalam fungsi yang akan dioptimalkan:

$A(x,y)= x y +\cfrac{\pi x^2}{8}\ \xrightarrow{y \ = \ \frac{40-2x- \pi x}{4} }$

$A(x)= x \cdot \cfrac{40-2x- \pi x}{4}+\cfrac{\pi x^2}{8}$

$A(x)= \cfrac{40x-2x^2-\pi x^2}{4}+\cfrac{\pi x^2}{8}$

Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

$A'(x)=\cfrac{(40-4x-2\pi x)\cdot 4 +(40x-2x^2- \pi x^2)\cdot 0 }{4^2} +\cfrac{2\pi x \cdot 8 + \pi x^2 \cdot 0}{8^2}$

$A'(x)=\cfrac{160-16x-8\pi x }{16} +\cfrac{16\pi x}{64}$

Langkah 3: Temukan titik kritisnya.

Untuk menemukan titik kritis dari fungsi tersebut, kita menyelesaikannya

$A'(x)=0:$

$A'(x)=0$

$\cfrac{160-16x-8\pi x }{16} +\cfrac{16\pi x}{64} = 0$

Ini adalah persamaan dengan pecahan, jadi kita mengalikan tiap suku dengan lcm penyebutnya untuk menghilangkan pecahannya:

$64 \cdot \cfrac{160-16x-8\pi x }{16} +64 \cdot \cfrac{16\pi x}{64} = 0$

$4\cdot ( 160-16x-8\pi x) +1\cdot 16\pi x= 0$

$640-64x -32 \pi x +16\pi x= 0$

$-64x -32 \pi x +16\pi x= -640$

$-64x -16 \pi x = -640$

$(-64 -16 \pi) x = -640$

$x=\cfrac{-640}{-64 -16 \pi} = 5,6$

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Untuk mempelajari kemonotonan suatu fungsi, kita nyatakan titik kritis di sebelah kanan:

$A'(0)=\cfrac{160-16\cdot 0-8\pi \cdot 0 }{16} +\cfrac{16\pi \cdot 0}{64} = 10 +0 = 10 \ \rightarrow \ \bm{+}$

$A'(6)=\cfrac{160-16\cdot 6-8\pi \cdot 6 }{16} +\cfrac{16\pi \cdot 6}{64} = -5,42 +4,71 = -0,71 \ \rightarrow \ \bm{-}$

Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:

Pertumbuhan:

$\bm{(-\infty , 5,6)}$

Mengurangi:

$\bm{(5,6,+\infty)}$

Fungsinya berubah dari naik ke turun pada x=5,6, jadi x=5,6 adalah maksimum dari fungsi tersebut.

Belum,

$x=5,6$

adalah nilai yang membuat permukaan maksimum. Sekarang kita menghitung nilai

$y :$

$y = \cfrac{40-2\cdot 5,6- \pi \cdot 5,6}{4} = 2,80$

Jadi, nilai permukaan maksimum adalah:

$\bm{x = 5,60} \ \mathbf{m}$

$\bm{y = 2,80} \ \mathbf{m}$

Masalah 6

Kami ingin membangun tangki berbentuk silinder dengan luas 54 cm ² . Tentukan jari-jari alas dan tinggi silinder agar volumenya maksimum.

Lihat solusinya

Langkah 1: Atur fungsi yang akan dioptimalkan.

Volume silinder dihitung dengan rumus berikut:

$V= A_{base}\cdot h$

Luas alasnya adalah lingkaran, jadi rumusnya adalah

$A_{\text{base}}=\pi r^2$

. Oleh karena itu, rumus volume silinder adalah:

$V= \pi r^2 \cdot h$

Kami sudah memiliki fungsi untuk mengoptimalkan. Tapi itu tergantung pada dua variabel (

$r$

Dan

$h$

) sementara itu hanya dapat bergantung pada satu. Namun pernyataan tersebut menyatakan bahwa luas silinder harus 54 cm ² , jadi kita akan memanfaatkan kondisi ini untuk mencari hubungan antara

$r$

Dan

$h .$

Untuk menghitung luas silinder Anda harus menjumlahkan luas lateralnya dengan luas kedua alasnya:

$A_{cilindro} = A_{lateral}+2A_{base} = 2\pi r h + 2\pi r^2$

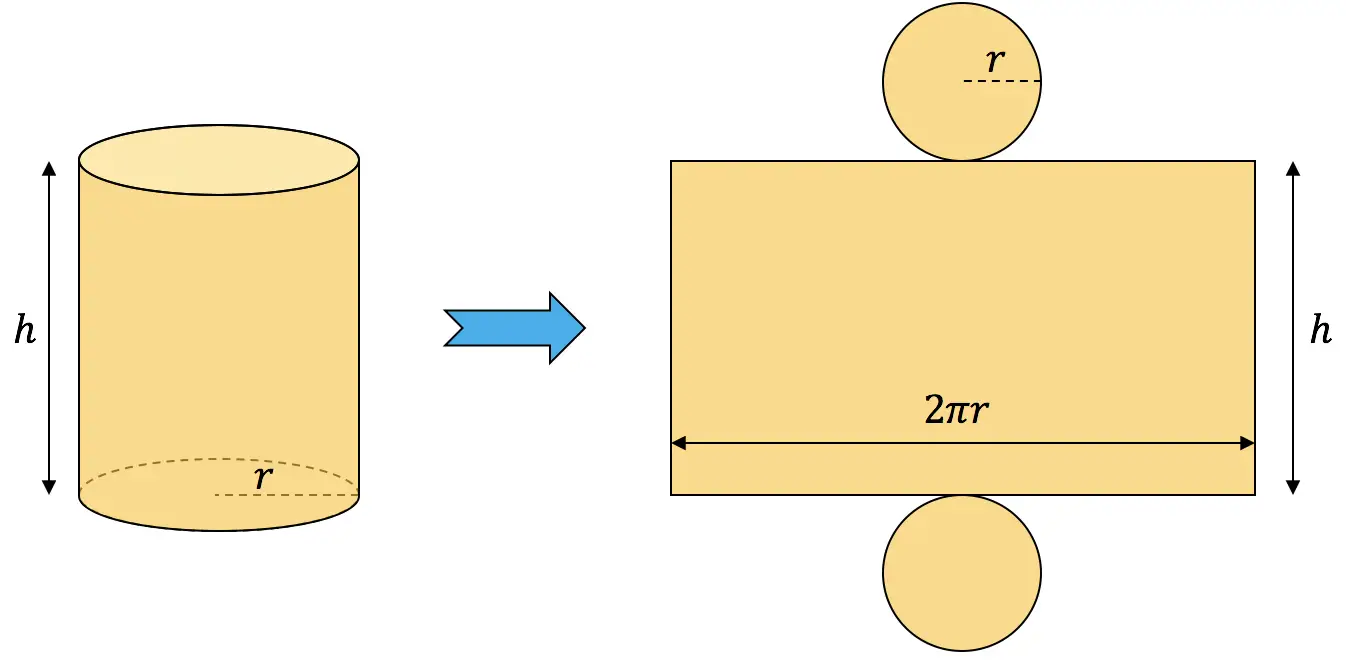
Luas silinder harus 54 cm ² , jadi kita atur ekspresi sebelumnya sama dengan 54 untuk mendapatkan hubungan antara

$r$

Dan

$h :$

$A_{cilindro} =2\pi r h + 2\pi r^2 = 54$

Kami membersihkan

$h :$

$2\pi r h = 54 - 2\pi r^2$

$h = \cfrac{54 - 2\pi r^2}{2\pi r}$

Dan kami mengganti ekspresi yang ditemukan dalam fungsi yang akan dioptimalkan:

$V= \pi r^2 \cdot h \xrightarrow{h \ = \ \frac{54 - 2\pi r^2}{2\pi r} } V = \pi r^2 \cdot \cfrac{54 - 2\pi r^2}{2\pi r}$

$V = \cancel{\pi} r^{\cancel{2}} \cdot \cfrac{54 - 2\pi r^2}{2 \cancel{\pi} \cancel{r}} =r \cdot \cfrac{54 - 2\pi r^2}{2}$

$V(r) = r \cdot (27 - \pi r^2)= 27r - \pi r^3$

Langkah 2: Hitung turunan dari fungsi yang akan dioptimalkan.

$V(r)=27r - \pi r^3\ \longrightarrow \ V'(r)= 27-3 \pi r^2$

Langkah 3: Temukan titik kritisnya.

Untuk menemukan titik kritis dari fungsi tersebut, kita menyelesaikannya

$V'(r)=0:$

$V'(r)=0$

$27-3 \pi r^2=0$

$-3 \pi r^2=-27$

$r^2=\cfrac{-27}{-3\pi }$

$r^2=2,86$

$\sqrt{r^2}=\sqrt{2,86}$

$r=1,69$

Langkah 4: Pelajari monotonisitas suatu fungsi dan tentukan maksimum atau minimum fungsi tersebut.

Untuk mempelajari monotonisitas suatu fungsi, kita nyatakan titik kritis yang terdapat pada garis bilangan:

$V'(0)= 27-3 \pi\cdot 0^2 = 27-0 = +27 \ \rightarrow \ \bm{+}$

$V'(2)= 27-3 \pi \cdot 2^2 = 27-37,70 = -10,70 \ \rightarrow \ \bm{-}$

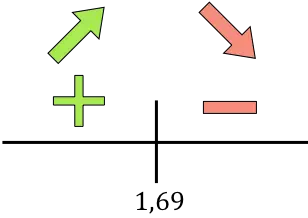
Jika turunannya positif berarti fungsinya meningkat, dan jika turunannya negatif berarti fungsinya menurun. Oleh karena itu, interval pertumbuhan dan penurunannya adalah:

Pertumbuhan:

$\bm{(-\infty,1,69)}$

Mengurangi:

$\bm{(1,69,+\infty)}$

Fungsinya berubah dari naik ke turun pada r=1,69, jadi r=1,69 cm adalah fungsi maksimumnya .

Oleh karena itu, r=1,69 adalah nilai jari-jari yang menghasilkan volume maksimum. Sekarang kita menghitung tingginya:

$h = \cfrac{54 - 2\pi \cdot 1,69^2}{2\pi \cdot1,69} = \cfrac{54 - 17,94}{10,62} = 3,39$

Jadi nilai yang menjadikan volume maksimum adalah:

Radio

$\bm{= r = 1,69} \ \mathbf{cm}$

Tinggi

$\bm{= h = 3,39} \ \mathbf{cm}$

Apa masalah optimasi?

Bagaimana mengatasi masalah optimasi

Contoh masalah optimasi

Masalah optimasi teratasi

Masalah 1

Masalah 2

Masalah 3

Masalah 4

Masalah 5

Masalah 6

Tinggalkan Komentar Batalkan Balasan