Di halaman ini Anda akan melihat cara mengurangkan dua vektor, baik secara grafis maupun numerik. Untuk menguranginya secara grafis, ada tiga metode: jajaran genjang, segitiga, dan poligon. Di sini Anda dapat membedakan kelebihan dan kekurangan masing-masing metode. Selain itu, Anda akan menemukan contoh, latihan, dan masalah yang diselesaikan langkah demi langkah.
Bagaimana cara mengurangi dua vektor secara grafis?
Ada beberapa cara untuk mengurangkan vektor secara geometri. Tentunya dengan semuanya diperoleh hasil yang sama, namun kami akan menjelaskan semua caranya kepada Anda sehingga Anda dapat memilih salah satu yang Anda sukai. 👌
Untuk mengurangkan 2 vektor saja, ada dua prosedur grafis: metode jajaran genjang dan metode segitiga . Namun, jika kita ingin menyelesaikan pengurangan 3 vektor atau lebih, kita perlu menggunakan metode poligon .
Jadi, tanpa basa-basi lagi, Anda sudah mendapatkan penjelasan dari semua cara tersebut di bawah ini.
Metode atau aturan jajar genjang
Aturan jajar genjang atau metode jajar genjang adalah prosedur yang memungkinkan Anda mencari pengurangan dua vektor melalui representasi grafisnya dengan cara yang sangat sederhana. Langkah-langkah yang harus diikuti untuk menerapkan proses ini adalah sebagai berikut:
- Pertama, kita nyatakan kedua vektor pada grafik dan posisikan keduanya pada titik penerapan yang sama, yaitu kita letakkan titik asal kedua vektor pada titik yang sama.
- Kedua, kita menggambar vektor yang berlawanan dengan vektor yang dikurangkan pada operasi tersebut, atau dengan kata lain kita membalik vektor yang melakukan pengurangan tersebut.
- Kemudian kita tarik garis sejajar dengan vektor yang berubah tanda di ujung vektor yang dijumlahkan. Dan kami ulangi prosesnya dengan vektor lainnya. Sehingga kita akan mendapatkan gambar jajar genjang (sesuai dengan nama aturannya).
- Terakhir, hasil pengurangannya adalah vektor yang bergerak dari titik asal kedua vektor hingga titik potong dua garis sejajar.
Perhatikan contoh umum berikut di mana dua vektor dikurangkan menggunakan metode jajaran genjang:
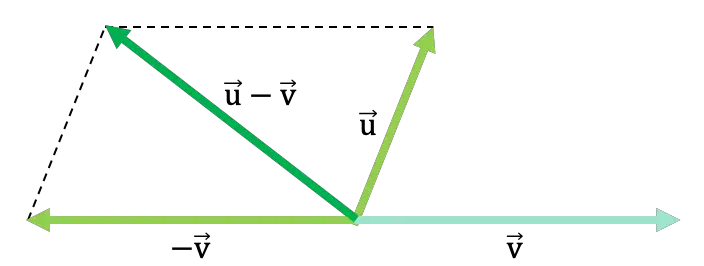
Metode atau aturan segitiga
Metode segitiga adalah prosedur lain yang dapat digunakan untuk mengurangkan dua vektor dari grafiknya. Dalam hal ini, langkah-langkah yang harus diikuti adalah:
- Tempatkan kedua vektor pada titik penerapan yang sama, yaitu kedua vektor mempunyai titik yang sama dengan titik asal.
- Hasil pengurangan vektor adalah ruas yang dimulai dari ujung vektor yang mengurangkan ke ujung vektor yang lain. Jika diperhatikan lebih dekat, sebuah segitiga selesai dengan pengurangan dua vektor dan pengurangan vektor.
Berikut contoh pengurangan vektor dengan metode segitiga:
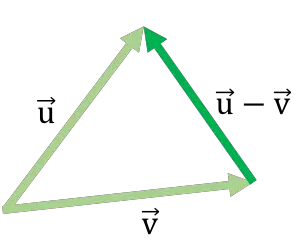
Cara pengurangan vektor ini mirip dengan metode kepala dan ekor yang digunakan untuk menjumlahkan vektor .
metode poligon
Setelah kita melihat cara menyelesaikan pengurangan dua vektor secara grafis, kita akan melihat cara menyelesaikan pengurangan dua vektor jika kita mempunyai lebih dari dua vektor.
Saat Anda ingin mengurangkan tiga vektor atau lebih, ada teknik untuk mempercepat penghitungan dan mengurangkan semua vektor sekaligus. Teknik ini disebut metode poligon dan terdiri dari penerapan metode penjumlahan vektor head-to-tail secara berturut-turut.
Sekarang Anda mungkin berpikir: menjumlahkan vektor? Itu salah dikoreksi… Ya tidak! eh eh
Ternyata mengurangkan dua buah vektor sama dengan menjumlahkan sebuah vektor ditambah vektor yang berlawanan (atau negatif) dari vektor yang mengurangkan tersebut. Hal ini disebabkan oleh sifat penjumlahan dan pengurangan vektor:
![]()
Oleh karena itu, langkah-langkah yang perlu kita ikuti untuk mengurangkan 3 vektor atau lebih dengan metode poligon adalah:
- Pertama, kita perlu mencari invers vektor dari setiap vektor pengurangan. Sesederhana membalikkan arah dan arah semua vektor yang dikurangi.
- Lalu kita tempatkan masing-masing vektor yang berlawanan di sebelah vektor yang tidak Anda kurangi, satu demi satu. Sehingga titik asal suatu vektor berimpit dengan ujung vektor yang lain.
- Terakhir, hasil pengurangan vektor adalah vektor yang diperoleh dengan menggabungkan titik awal vektor pertama dengan ujung vektor terakhir.
Perhatikan contoh berikut dimana pengurangan dilakukan dengan 4 vektor:
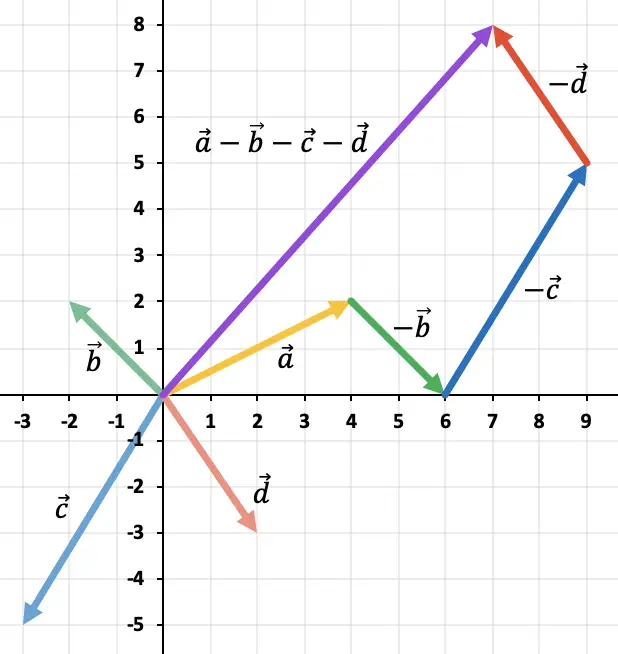
Perhatikan bahwa untuk mencari vektor yang berlawanan dari suatu vektor, kedua komponen vektor tersebut harus berubah tanda.
Bagaimana cara menghitung pengurangan dua vektor secara numerik?
Setelah kita mengetahui cara mengurangkan vektor dari grafik, kita akan melihat cara menghitung pengurangan vektor secara numerik atau aljabar.
Untuk mengurangkan dua vektor secara numerik, Anda harus mengurangkan masing-masing komponennya. Atau dengan kata lain koordinat X kedua vektor tersebut dikurangkan satu sama lain begitu pula dengan koordinat Y.
![]()
![]()
Misalnya pengurangan antar vektor
![]()
Dan
![]()
Timur:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(4,1) -(2, 3) \\[2ex] & = (4-2,1-3) \\[2ex] & = \bm{(2,-2)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5497555b19f5d230433a622a03704ee_l3.png)
Menyelesaikan Masalah Pengurangan Vektor
Latihan 1
Hitung pengurangan vektor secara grafis
![]()
lebih sedikit
![]()
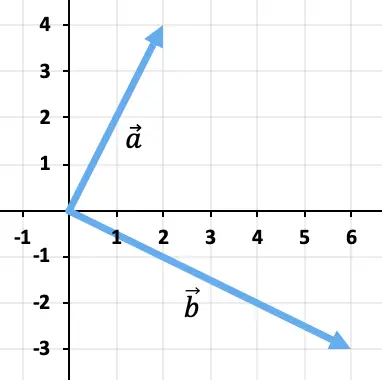
Untuk mengurangkan kedua vektor tersebut, kita akan menggunakan metode segitiga. Titik-titik tersebut sudah ditempatkan pada titik penerapan yang sama (asal koordinat), sehingga hasil pengurangannya adalah vektor yang berangkat dari ujung
![]()
pada akhir
![]()
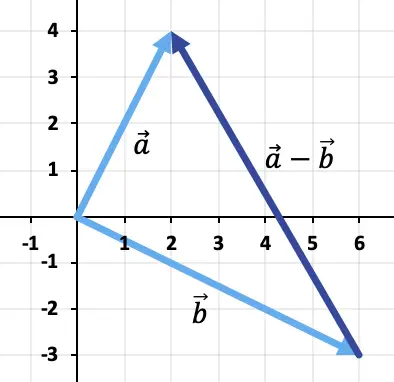
Latihan 2
Temukan pengurangan vektor secara grafis
![]()
lebih sedikit
![]()
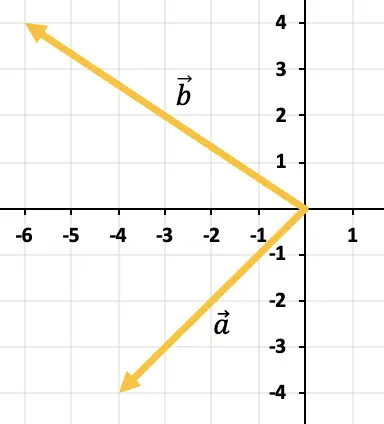
Untuk mengurangkan kedua vektor, kita akan menggunakan aturan segitiga. Titik-titik tersebut sudah ditempatkan pada titik penerapan yang sama (di awal sumbu X dan sumbu Y), sehingga hasil pengurangannya adalah vektor yang berangkat dari akhir
![]()
pada akhir
![]()
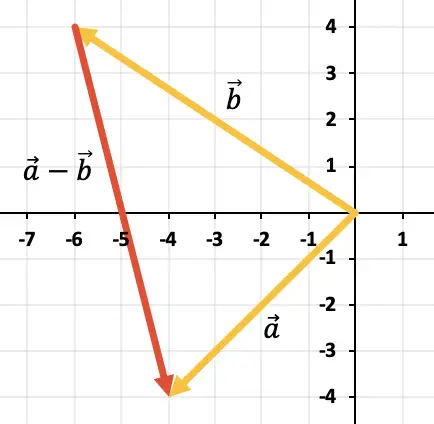
Latihan 3
Selesaikan operasi vektor berikut secara grafis:
![]()
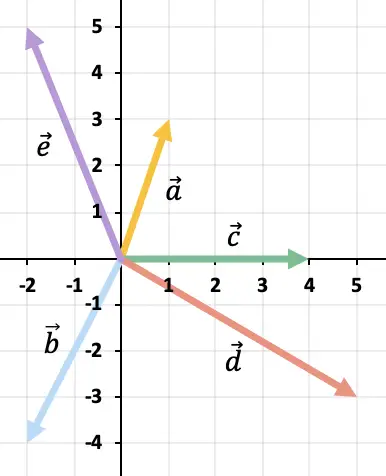
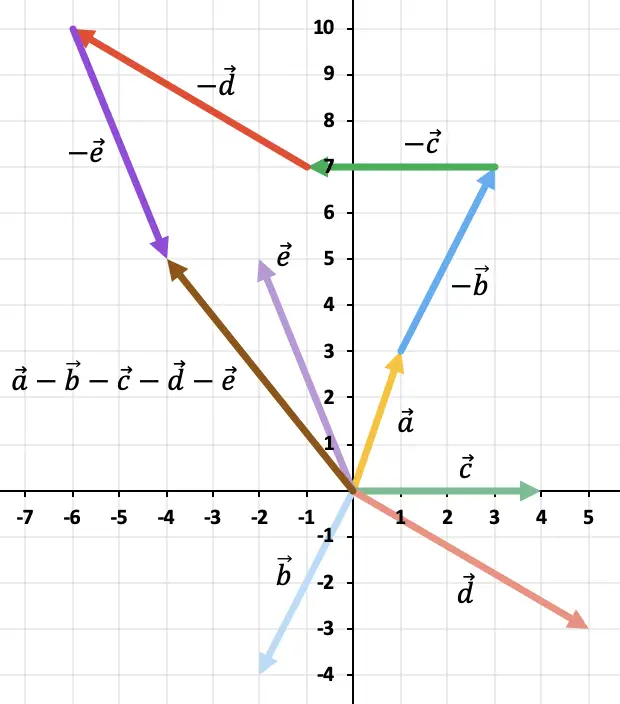
Karena terdapat lebih dari 2 vektor, kita akan menggunakan aturan poligon untuk menyelesaikan pengurangan vektor. Untuk melakukan ini, kita perlu merepresentasikan vektor-vektor yang berlawanan dari vektor-vektor yang tersisa satu demi satu. Dan hasilnya adalah vektor yang dimulai dari titik asal vektor tersebut
![]()
ke tempat ujung vektor lawan terakhir.
Latihan 4
Tentukan secara numerik hasil pengurangan vektor-vektor berikut:
![]()
![]()
Untuk mengurangkan dua vektor secara numerik, Anda harus mengurangkan koordinatnya masing-masing:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}-\vv{b}& =(-1,5)-(3,-2) \\[2ex] & = (-1-3 ,5-(-2))\\[2ex] & = (-4 ,5+2)\\[2ex] & =\bm{(-4,7)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b64aac805c6565b57ac1d33977988013_l3.png)
Latihan 5
Selesaikan operasi vektor berikut secara analitis:
![]()
![]()
Untuk mengurangkan vektor secara numerik (atau analitis) kita harus mengurangkan masing-masing komponennya:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}-\vv{b}-\vv{d}-\vv{d}& =(2,4)-(-1,4)-(0,2)-(3,-7) \\[2ex] & =(3,0)-(0,2)-(3,-7) \\[2ex] & =(3,-2)-(3,-7) \\[2ex]& =\bm{(0,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa640e47728e968a9626c295f237f93c_l3.png)