▷ Cara mengetahui apakah suatu fungsi kontinu (latihan terselesaikan)

Pada artikel kali ini kami akan menjelaskan apa itu fungsi kontinu dan cara menentukan kontinuitas suatu fungsi di suatu titik atau tidak. Selain itu, Anda akan menemukan properti fungsi kontinu dan analisis kontinuitas fungsi paling umum. Terakhir, Anda dapat berlatih dengan latihan yang diselesaikan pada fungsi kontinu untuk memahami konsep sepenuhnya.

Apa yang dimaksud dengan fungsi kontinu?

Kontinuitas suatu fungsi dapat dipelajari secara grafis. Fungsi kontinu adalah fungsi yang dapat direpresentasikan dalam grafik tanpa perlu mengeluarkan pensil dari kertas.

Fungsi berkelanjutan

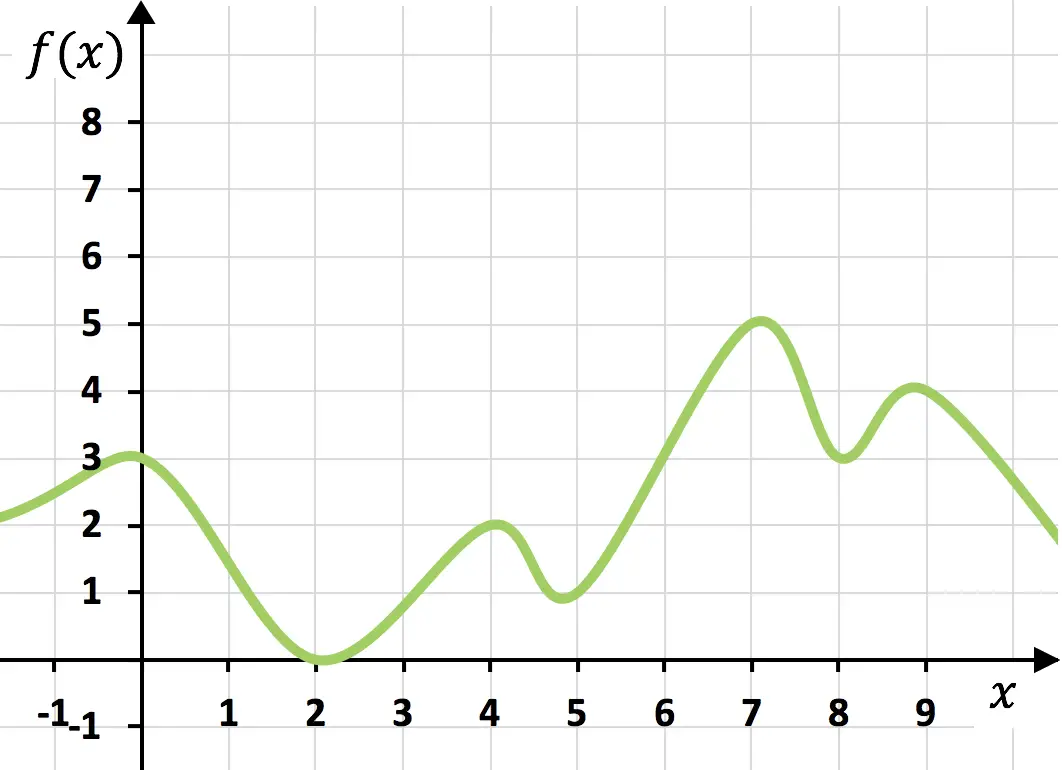
Fungsi di atas bersifat kontinu karena dapat digambar dalam satu goresan tanpa perlu mengangkat tangan dari kertas.

Sebaliknya, jika kondisi kontinuitas sebelumnya tidak dimasukkan ke dalam suatu fungsi, maka disebut fungsi diskontinyu .

Fungsi terputus-putus

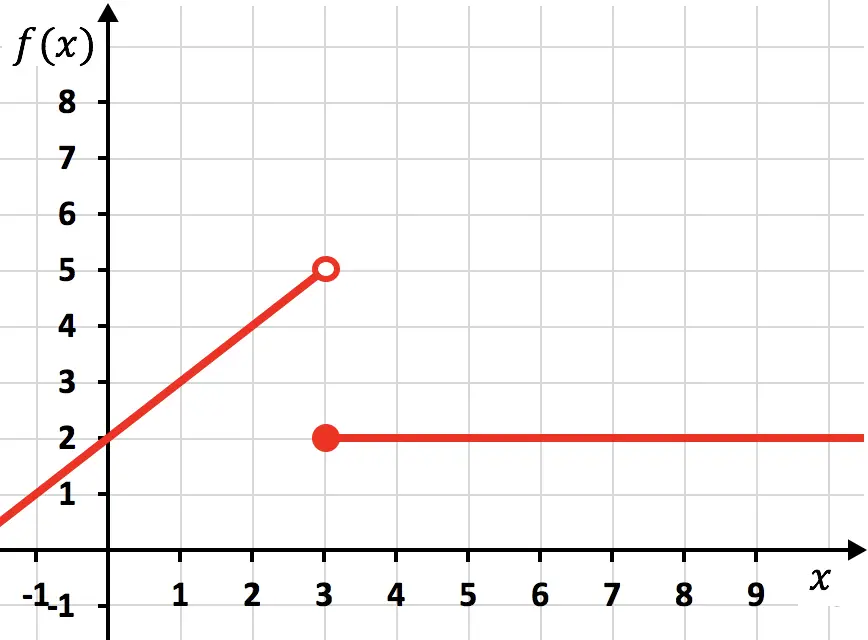
Fungsi sebelumnya terputus-putus karena untuk merepresentasikannya harus membuat dua garis dengan pensil. Dalam hal ini, fungsi tersebut tidak lagi kontinu di x=3, oleh karena itu kita katakan bahwa x=3 adalah titik diskontinuitas .

Selain itu, ada tiga jenis diskontinuitas : diskontinuitas yang dapat dihindari, diskontinuitas lompat hingga yang tak terelakkan, dan diskontinuitas lompat tak terelakkan. Di tautan berikut Anda dapat melihat seperti apa masing-masing jenis diskontinuitas dan apa perbedaannya:

➤ Lihat: jenis diskontinuitas

Kontinuitas suatu fungsi pada suatu titik

Setelah kita melihat seperti apa grafik fungsi kontinu, kita akan melihat cara mengetahui apakah suatu fungsi kontinu atau tidak secara analitis.

Secara matematis, suatu fungsi kontinu di suatu titik jika memenuhi tiga syarat berikut:

Fungsinya ada pada titik ini, yaitu bayangan titik tersebut ada.

$\exists \ f(a)$

Ada batasan fungsi pada saat ini. Oleh karena itu, batas lateral kiri dan kanan fungsi pada titik ini adalah sama.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

Bayangan suatu titik berimpit dengan limit fungsi pada titik tersebut.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

Jadi, jika ketiga syarat kontinuitas terpenuhi di semua titik suatu fungsi, maka fungsi tersebut kontinu.

Sebagai contoh, kita akan menganalisis kontinuitas fungsi perataan berikut:

kontinuitas suatu fungsi yang ditentukan sedikit demi sedikit

Bahkan jika Anda mengubah bagian, pada intinya

$x=-2$

Fungsi tersebut kontinu, karena batas lateral fungsi pada titik ini sama dan lebih bertepatan dengan nilai fungsi pada titik ini.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

Sebaliknya, fungsi tersebut tidak kontinu di suatu titik

$x=4$

karena kedua batas lateralnya berbeda sehingga limit fungsinya tidak ada pada titik ini:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

Singkatnya, fungsi yang didefinisikan oleh potongan-potongan tersebut kontinu di semua bilangan real kecuali di

$x=4,$

dimana terdapat diskontinuitas.

Kami juga dapat memverifikasi bahwa fungsi tersebut terputus-putus

$x=4$

karena untuk merepresentasikannya secara grafis, pensil harus dikeluarkan dari kertas pada saat ini.

Kontinuitas fungsi dasar

Jenis fungsi tertentu bersifat kontinu berdasarkan karakteristiknya:

Fungsi konstanta kontinu pada semua bilangan real.

$f(x)=k$

Fungsi polinomial kontinu untuk semua bilangan real.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Fungsi rasional (atau pecahan) kontinu pada semua bilangan real kecuali pada nilai yang menghilangkan penyebut pecahan, pada titik tersebut fungsi tersebut menyajikan diskontinuitas.

$f(x)=\cfrac{p(x)}{q(x)}$

Fungsi eksponensial kontinu pada semua bilangan real:

$f(x)=a^x$

Fungsi logaritma kontinu di semua titik yang argumennya positif.

$f(x)=\log_a (x)$

Kontinuitas fungsi irasional , atau fungsi dengan akar, bergantung pada indeks akar (n). Jika indeksnya genap, ini adalah fungsi kontinu di semua titik yang membuat argumen akar sama dengan atau lebih besar dari nol. Tetapi jika indeksnya ganjil, maka keduanya merupakan fungsi kontinu pada semua bilangan real.

$f(x)=\sqrt[n]{x}$

Kontinuitas fungsi trigonometri bergantung pada jenis fungsinya. Fungsi sinus dan fungsi kosinus kontinu pada himpunan bilangan real, tetapi fungsi tangennya diskontinu pada titik-titiknya.
$\displaystyle x=\frac{\pi}{2}+k\pi$

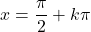
(di mana k adalah bilangan bulat).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

Sifat-sifat fungsi kontinu

Sean

$f(x)$

Dan

$g(x)$

dua fungsi kontinu pada suatu titik

$x=a,$

Berikutnya:

Jumlah dua fungsi kontinu di suatu titik merupakan fungsi kontinu lainnya di titik tersebut.

$f(x)+g(x)$

Hasil kali dua fungsi kontinu di suatu titik sama dengan fungsi kontinu lainnya di titik tersebut.

$f(x)\cdot g(x)$

Membagi dua fungsi kontinu pada suatu titik akan menghasilkan fungsi kontinu lainnya pada titik tersebut, selama titik tersebut tidak menghilangkan fungsi pembagian tersebut.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

Susunan dua fungsi kontinu pada suatu titik menimbulkan fungsi kontinu pada titik yang sama.

$f(x)\circ g(x)$

➤ Lihat: apa itu fungsi komposit?

Latihan soal kesinambungan suatu fungsi

Latihan 1

Temukan diskontinuitas fungsi yang ditunjukkan pada grafik berikut. Tentukan juga jenis diskontinuitasnya.

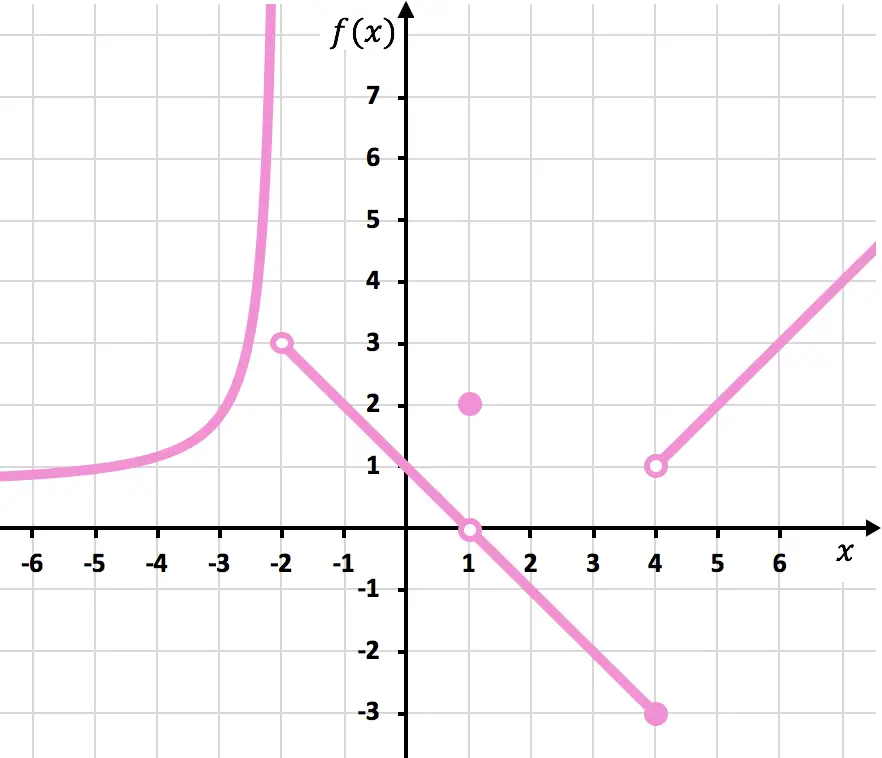
latihan menyelesaikan diskontinuitas fungsi

Catatan: untuk melakukan latihan ini kami menyarankan Anda terlebih dahulu melihat apa saja jenis-jenis diskontinuitas dan bagaimana cara mengidentifikasinya. Penjelasannya dapat Anda lihat pada tautan prinsip tipe diskontinuitas .

Lihat solusinya

Untuk menggambar fungsinya Anda harus menaikkan pensil di x=-2, di x=1 dan di x=4. Oleh karena itu, fungsinya terputus-putus pada ketiga titik ini.

Pada x=-2, limit ruas kirinya adalah +∞ dan limit ruas kanannya adalah 3. Jadi, karena salah satu limit sisinya tidak terhingga, fungsi tersebut mempunyai diskontinuitas lompat tak terhingga pada x=-2.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

Limit fungsi di x=1 adalah 0 dan, sebaliknya, nilai fungsi di x=1 sama dengan 2. Oleh karena itu, fungsi tersebut menyajikan diskontinuitas yang dapat dihindari di x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

Pada x = 4, limit ruas kirinya adalah -3 dan limit ruas kanannya adalah 1. Oleh karena itu, karena kedua limit sisi tersebut berbeda dan tidak ada satu pun yang menghasilkan tak terhingga, maka fungsi tersebut pasti memiliki diskontinuitas lompatan berhingga di x =4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Latihan 2

Tentukan titik-titik di mana fungsi yang ditunjukkan pada grafik berikut diskontinu.

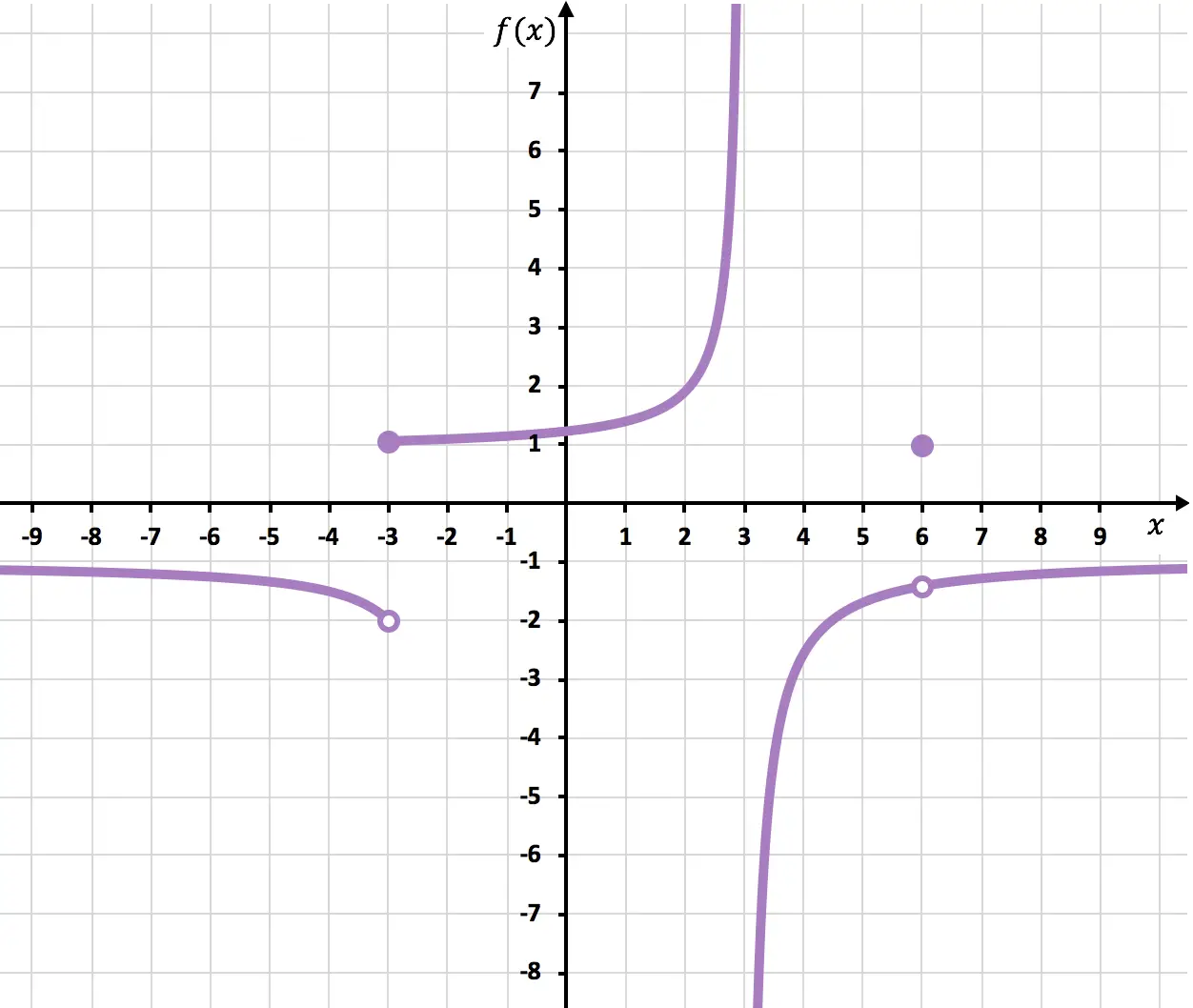
menyelesaikan latihan tentang jenis-jenis diskontinuitas suatu fungsi

Lihat solusinya

Pada titik x=6 fungsinya terputus karena terdapat titik terbuka. Limit saat x mendekati 6 adalah -1,4 tetapi f(6)=1. Oleh karena itu, fungsi tersebut mempunyai diskontinuitas yang dapat dihindari pada x=6 karena nilai limitnya tidak sesuai dengan nilai fungsi:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

Pada x=-3 batas lateralnya tidak berimpit dan tidak ada yang menghasilkan tak terhingga. Oleh karena itu, fungsi tersebut memiliki diskontinuitas lompatan terbatas yang tak terelakkan pada x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

Dan yang terakhir, fungsi tersebut mempunyai diskontinuitas lompatan tak terhingga pada x = 3, karena setidaknya satu batas lateral pada titik ini menghasilkan tak terhingga.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Latihan 3

Analisislah kontinuitas fungsi rasional berikut:

$\displaystyle f(x)= \frac{2}{x-5}$

Lihat solusinya

Fungsi rasional kontinu di seluruh domainnya, yaitu di semua bilangan real kecuali nilai yang menghilangkan penyebutnya. Oleh karena itu, kita menetapkan penyebut fungsi rasional sama dengan nol untuk melihat titik mana yang tidak termasuk dalam domain:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

Oleh karena itu, fungsi tersebut kontinu di semua titik kecuali x=5.

Latihan 4

Analisislah kontinuitas fungsi perataan berikut:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

Lihat solusinya

Fungsinya juga kontinu di bagian pertama,

$5x-2$

, seperti pada bagian kedua,

$x^2+2$

, karena merupakan fungsi polinomial.

Jadi, satu-satunya titik di mana suatu fungsi dapat diskontinu adalah titik di mana fungsi tersebut terputus sebagian. Jadi mari kita hitung batas lateral pada titik ini:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

Oleh karena itu kedua limit lateralnya berimpit, limit fungsi ketika x cenderung 1 sama dengan 3:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

Selanjutnya bayangan x=1 juga 3:

$f(1)=1^2+2=\bm{3}$

Jadi, karena limit fungsi di x=1 sama dengan bayangan titik tersebut, maka fungsi tersebut kontinu di titik x=1. Oleh karena itu, bilangan ini kontinu pada semua bilangan real.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

Latihan 5

Pelajari kesinambungan fungsi irasional berikut:

$f(x)=\sqrt{2x+6}$

Lihat solusinya

Merupakan fungsi radikal yang indeksnya genap, sehingga fungsi tersebut akan kontinu selama argumen akarnya lebih besar dari 0 (karena akar kuadrat dari suatu bilangan negatif tidak ada):

$2x+6\ge 0$

Kami menyelesaikan pertidaksamaan:

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

Penyelesaiannya terdiri dari semua bilangan yang lebih besar atau sama dengan -3. Oleh karena itu, fungsi tersebut kontinu pada interval domainnya:

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

Latihan 6

Analisislah kontinuitas fungsi logaritma berikut:

$f(x)=\log_3 (-3x+6)$

Lihat solusinya

Ini adalah fungsi logaritma, dan tidak ada logaritma bilangan negatif maupun logaritma 0. Oleh karena itu, fungsi tersebut akan ada selama argumen logaritmanya positif (lebih besar dari nol):

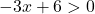$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Kami menyelesaikan pertidaksamaan:

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{-6}{-3}$

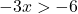
Ingatlah bahwa ketika suatu bilangan negatif dibagi dengan sisi lain pertidaksamaan, tanda pertidaksamaannya harus dibalik.

$x<2$

Solusinya terdiri dari semua bilangan yang kurang dari 2. Oleh karena itu, domain definisi fungsi tersebut adalah:

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

Oleh karena itu, fungsi tersebut kontinu di setiap titik dalam domainnya.

Latihan 7

Hitunglah kontinuitas fungsi berikut:

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

Lihat solusinya

Pada penyebut pecahan kita mempunyai akar dengan indeks genap, sehingga fungsi tersebut akan ada setiap kali isi akar sama dengan atau lebih besar dari nol:

$-2x-8\geq 0$

Tapi juga, akarnya ada pada penyebut pecahan, dan penyebut pecahan tidak akan pernah sama dengan 0. Jadi fungsinya hanya akan ada jika isi akarnya lebih besar dari 0:

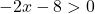$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Sekarang kita selesaikan pertidaksamaan tersebut:

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{8}{-2}$

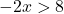
Ingatlah bahwa ketika kita mengubah sisi suatu bilangan negatif dengan mengalikan atau membagi suatu pertidaksamaan, kita juga harus memutar tanda pertidaksamaannya.

$x<-4$

Hasilnya semua angka kurang dari -4. Jadi domain dari fungsi tersebut, dan kontinuitasnya, ditentukan oleh interval berikut:

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

Latihan 8

Hitung nilai k agar fungsi tersebut kontinu sepanjang

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$

Lihat solusinya

Agar fungsi tersebut kontinu, kedua batas lateral pada titik putus harus memberikan hasil yang sama. Oleh karena itu, pertama-tama kita menghitung batas lateral pada titik putus bagian yang tidak mempunyai k :

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

Oleh karena itu, agar fungsi sepotong-sepotong kontinu, batas sisi lainnya juga harus sama dengan 7.

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

Jadi, agar suatu fungsi kontinu, dua batas lateral suatu titik harus memberikan hasil yang sama. Oleh karena itu, ekspresi yang diperoleh dari limit tersebut kita tetapkan sama dengan 7 (hasil dari limit lateral lainnya).