Pada halaman ini Anda akan melihat apa itu matriks kompleks, matriks konjugasi, dan matriks transpos konjugasi. Sekarang mereka sangat mirip dengan Anda, tetapi Anda akan melihat bagaimana di akhir halaman Anda akan sepenuhnya memahami perbedaan di antara masing-masingnya. Selain itu, kita akan melihat contoh setiap jenis dan propertinya.
matriks yang kompleks
Sebelum melihat penjelasan matriks konjugasi dan transpos matriks konjugasi, mari kita ulas dulu konsep matriks kompleks:
Apa itu matriks kompleks?
Matriks kompleks adalah matriks yang mempunyai bilangan kompleks tertentu diantara elemen-elemennya.
Ingatlah bahwa bilangan kompleks atau bilangan imajiner adalah bilangan yang terdiri dari bagian nyata dan bagian imajiner, yang ditandai dengan huruf i. Misalnya:
![]()
.
Contoh matriks kompleks
Mari kita lihat beberapa contoh array multidimensi kompleks:
Contoh matriks kompleks berorde 2×2
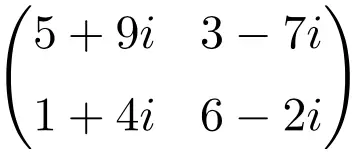
Contoh matriks kompleks berdimensi 3×3
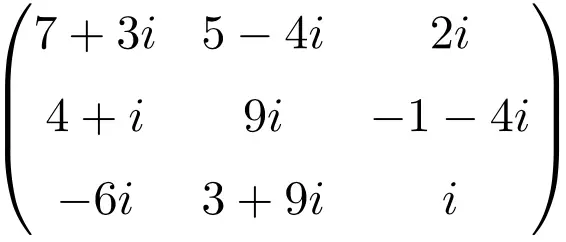
Contoh matriks kompleks berukuran 4×4
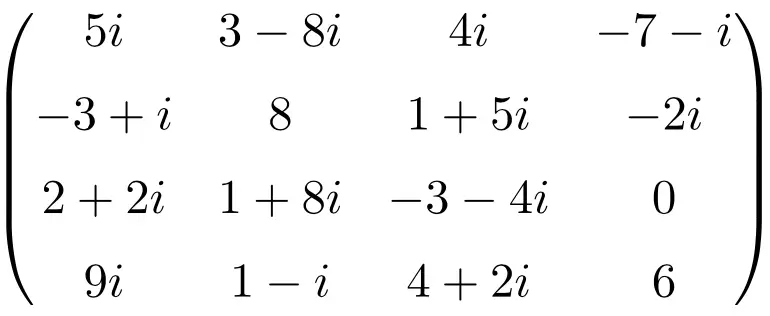
matriks konjugasi
Setelah kita mengetahui pengertian matriks kompleks, mari kita lihat apa itu matriks konjugasi dan matriks konjugasi transpos:
Apa itu matriks konjugasi?
Matriks konjugasi adalah matriks kompleks yang semua elemennya telah digantikan oleh konjugatnya, yaitu tanda bagian imajiner dari semua bilangan kompleksnya telah diubah.
Matriks konjugat dari
![]()
dinyatakan dengan garis horizontal di atas:
![]()
.
Contoh matriks konjugasi
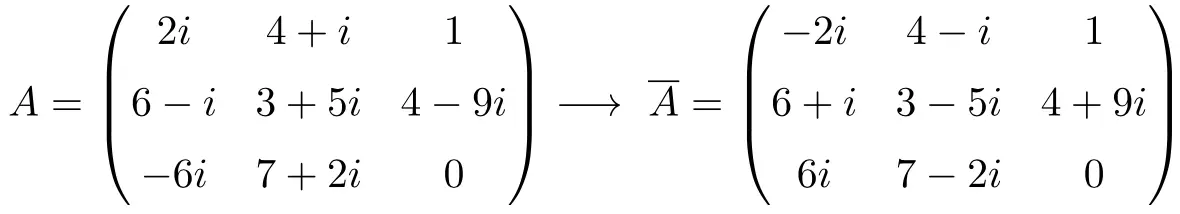
Sifat-sifat matriks konjugasi
Ciri-ciri matriks jenis ini adalah sebagai berikut:
- Konjugat suatu matriks konjugasi adalah matriks aslinya.
![]()
- Menjumlahkan (atau mengurangkan) dua matriks dan mengkonjugasikan hasilnya sama dengan mengkonjugasikan kedua matriks terlebih dahulu secara terpisah lalu menjumlahkan (atau mengurangkan) matriks tersebut.
![]()
- Hasil kali konjugasi dua matriks sama dengan mengkonjugasikan kedua matriks secara terpisah kemudian menghitung perkalian matriksnya.
![]()
- Mengalikan matriks dengan skalar dan mengkonjugasikan hasilnya sama dengan melakukan konjugasi skalar dan matriks terlebih dahulu, kemudian menyelesaikan hasil kali.
![]()
- Mentransposisi suatu matriks dan kemudian mengkonjugasikannya berarti mengkonjugasikan matriks terlebih dahulu kemudian mentransposisikannya.
![]()
- Melakukan invers suatu matriks kemudian mengkonjugasikannya sama dengan mengkonjugasikan matriks kemudian menginversinya.
![]()
- Pangkat suatu matriks konjugasi sama dengan pangkat matriks tak terkonjugasi yang sama.
![]()
- Menghitung jejak matriks terkonjugasi atau menghitung jejak matriks yang sama tanpa konjugasi dan kemudian mengkonjugasikan hasilnya adalah hal yang berbeda.
![]()
- Terakhir, mengambil determinan suatu matriks konjugasi sama dengan menghitung konjugat dari hasil determinan matriks yang sama tanpa konjugasi.
![]()
Konjugasi matriks transpos
Terakhir, setelah melihat cara mengkonjugasikan suatu matriks, mari beralih ke konsep matriks transpos terkonjugasi:
Apa yang dimaksud dengan matriks transpos konjugasi (atau transpos)?
Matriks konjugat yang ditransposisikan (atau ditransposisikan) adalah yang diperoleh setelah suatu matriks ditransposisikan kemudian dibuat konjugasinya.
Matriks jenis ini disebut juga matriks adjoint atau sederhananya matriks adjoint. Selain itu, biasanya diwakili oleh tanda bintang
![]()
, meskipun ada ahli matematika yang menggambarkannya sebagai
![]()
salah satu
![]()
.
Contoh Matriks Transpos Konjugasi
Berikut adalah contoh penghitungan transpos (atau transpos konjugasi) suatu matriks:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
Pertama-tama kita transpos matriks A:
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
Lalu kita hitung matriks konjugasi transposnya, atau dengan kata lain kita ubah tanda bagian imajiner semua bilangan kompleks:
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
Oleh karena itu, ringkasan perhitungan matriks transpos konjugasinya adalah:
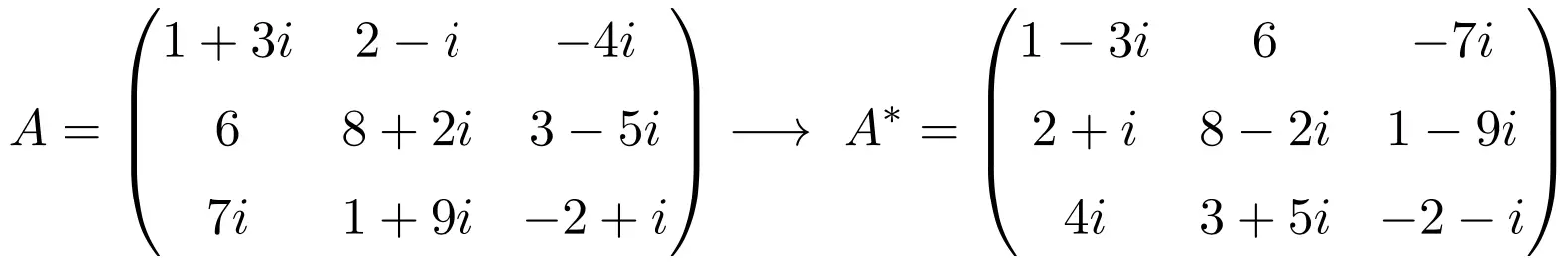
Sifat-sifat matriks transpos konjugasi
Sifat-sifat matriks persegi jenis ini adalah sebagai berikut:
- Matriks transpos terkonjugasi dari matriks yang ditransposisi dan terkonjugasi sebelumnya adalah matriks asal.
![]()
- Sifat penjumlahan transpos konjugasi matriks menyatakan bahwa menjumlahkan (atau mengurangkan) dua matriks dan kemudian menerapkan operasi ini pada hasilnya sama dengan terlebih dahulu melakukan transpos konjugasi setiap matriks lalu menjumlahkan (atau mengurangkan) hasilnya.
![]()
- Mengalikan dua matriks kemudian melakukan transpos konjugasinya memberikan hasil yang sama dengan hasil perkalian invers matriks transpos konjugasinya.
![]()
- Menghitung transpos konjugasi matriks hasil kali skalar dan matriks sama dengan mengkonjugasikan bilangan kompleks dan mencari transpos konjugasi matriks secara terpisah lalu mengalikannya.
![]()
- Jika matriks dapat dibalik, urutan pelaksanaan operasi inversi matriks dan transpos konjugasi tidak relevan.
![]()