▷ Komposisi fungsi (atau fungsi gabungan)

Pada artikel ini, kami akan menjelaskan apa itu fungsi komposit (atau komposisi fungsi). Selain itu, Anda akan dapat melihat beberapa contoh fungsi gabungan dan cara menghitung domain fungsi jenis ini. Terakhir, Anda akan menemukan properti komposisi fungsi dan beberapa latihan langkah demi langkah untuk dipraktikkan.

Apa itu komposisi fungsi?

Komposisi fungsi terdiri dari evaluasi secara berturut-turut nilai yang sama dari variabel bebas (x) dalam dua fungsi atau lebih. Misalnya, menyusun fungsi (gof)(x) menghasilkan fungsi komposit g[f(x)].

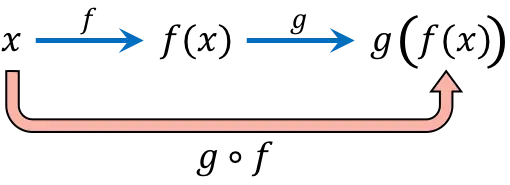
Ekspresi fungsi komposit

$g\circ f$

kita membaca “f disusun dengan g” atau “f diikuti oleh g”.

Perhatikan bahwa urutan penting dalam komposisi fungsi, fungsi di sebelah kanan simbol komposisi diterapkan terlebih dahulu

$(f)$

lalu fungsinya di sebelah kiri simbol komposisi

$(g).$

Contoh komposisi fungsi

Mengingat definisi fungsi komposit, mari kita lihat contoh cara menghitung komposisi dua fungsi.

Mengingat dua fungsi berbeda berikut:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Hitung fungsi gabungan

$\left(g \circ f\right)(x)$

dan mengevaluasinya

$x=3.$

Komposisi fungsi

$\left(g \circ f\right)(x)$

Ini berarti kita perlu melakukan fungsi komposit berikut:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Untuk mengatasinya kita ganti

$f(x)$

dengan ekspresi aljabarnya:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

Dan sekarang kita mengambil fungsi dari

$g(x)=\cfrac{x+4}{2}$

dan kami memasang ekspresi

$3x+1$

dimana ada satu

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

Dengan cara ini kita telah menghitung fungsi f yang terdiri dari g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Terakhir, untuk mengevaluasi fungsi komposit di

$x=3$

Cukup hitung gambar fungsi dalam nilai tersebut:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Domain fungsi komposit

Biasanya, ketika kita melakukan operasi pada suatu fungsi, domain dari fungsi yang dihasilkan adalah perpotongan domain dari fungsi aslinya. Namun sifat ini tidak dipenuhi oleh komposisi fungsi.

Domain komposisi fungsi

$(g\circ f)(x)$

ekuivalen dengan himpunan semua nilai x pada domain fungsi

$f$

seperti

$f(x)$

termasuk dalam domain fungsi

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Oleh karena itu, untuk menghitung domain suatu fungsi komposit, pertama-tama Anda harus mencari domain masing-masing fungsi secara terpisah, lalu domain fungsi yang dihasilkan dari operasi tersebut. Dengan demikian, domain komposisi fungsi akan terdiri dari semua nilai yang memenuhi kondisi matematika sebelumnya.

Ingat, jika kamu menemui masalah yang kamu tidak tahu cara mengatasinya, kamu bisa bertanya kepada kami di kolom komentar di bawah!

Sifat komposisi fungsi

Fungsi komposit mempunyai ciri-ciri sebagai berikut:

Komposisi fungsi mempunyai sifat asosiatif, oleh karena itu persamaan berikut selalu benar:

$f\circ (g\circ h)=(f\circ g)\circ h$

Secara umum komposisi fungsi tidak bersifat komutatif, sehingga urutan operasi menentukan hasilnya:

$f\circ g\neq g\circ f$

Unsur netral susunan fungsi berhubungan dengan fungsi identitas
$f(x)=x.$

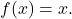
Jadi, setiap fungsi yang disusun dengan fungsi identitas menghasilkan fungsi itu sendiri:

$f\circ id = id \circ f = f$

$id = x$

Menghitung invers komposisi dua fungsi sama dengan mencari invers masing-masing fungsi terlebih dahulu, lalu menentukan fungsi kompositnya:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Fungsi invers juga berperan sebagai elemen simetris dari fungsi majemuk, karena komposisi suatu fungsi dengan inversnya ekuivalen dengan fungsi identitas:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

Turunan komposisi dua fungsi dihitung menggunakan aturan rantai:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Lihat:apa aturan rantainya?

Latihan soal komposisi fungsi

Latihan 1

Mengingat dua fungsi berikut:

$f(x)=x-2 \qquad g(x)= 5x + 4$

Hitung komposisi fungsi f yang tersusun dengan g dan g yang tersusun dengan f .

$(g\circ f)(x)$

$(f\circ g)(x)$

Lihat solusinya

Komposisi fungsi

$\left(g \circ f\right)(x)$

berarti menghitung fungsi komposit berikut:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Jadi untuk mengatasinya kita ganti

$f(x)$

untuk ekspresinya:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

DAN

$g\Big(x-2\Big)$

Artinya dalam ungkapan

$g(x) =5x+4$

Anda perlu mengganti variabel

$x$

Untuk

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Belum:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Di sisi lain, untuk mencari fungsi g yang terdiri dari f Anda harus melakukan prosedur yang sama tetapi dengan urutan terbalik:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Latihan ini juga menunjukkan sifat bahwa fungsi komposit tidak bersifat komutatif, karena hasilnya bergantung pada urutan penerapan fungsi tersebut.

Latihan 2

Mengingat dua fungsi berikut:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Menghitung komposisi fungsi f yang disusun dengan g .

$(g\circ f)(x)$

Lihat solusinya

Fungsi f yang terdiri dari g berarti menyelesaikan fungsi gabungan berikut:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Oleh karena itu kami mengganti fungsi f(x) dengan ekspresinya:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

Dan sekarang kita harus menggantinya

$x$

Untuk

$x^2-3$

dalam ekspresi fungsi g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

Singkatnya, hasil komposisi fungsinya adalah:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Latihan 3

Diketahui dua fungsi kuadrat berikut:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Tentukan hasil komposisi fungsi berikut:

$(g\circ f)(2)$

Lihat solusinya

$\left(g \circ f\right)(2)$

terdiri dari mencari fungsi komposit berikut:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Jadi untuk menyelesaikan fungsi komposit kita hitung dulu

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Oleh karena itu, sebagai

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Jadi untuk mencari nilai fungsi komposit Anda tinggal menghitungnya saja

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

Ringkasnya, hasil dari soal komposisi fungsi adalah:

$\bm{\left(g \circ f\right)(2) =8}$

Latihan 4

Mengingat dua fungsi berikut:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Tentukan hasil g yang disusun dengan f di x=2:

$(f\circ g)(2)$

Lihat solusinya

Dalam hal ini, kita harus menghitung fungsi komposit berikut:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Jadi pertama-tama kita temukan

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

Jadi, seperti

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Jadi untuk menyelesaikan fungsi komposit kita perlu menghitung

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$

Kesimpulannya, hasil pelaksanaan fungsi majemuk adalah:

$\bm{\left(f \circ g\right)(2)=1}$

Latihan 5

Mengingat tiga fungsi berikut:

$f(x) = x+1 \qquad g(x)= 3x - 5\qquad h(x) = \sqrt{x} - 3$

Hitung komposisi 3 fungsi berikut:

$(h \circ g \circ f )(x)$

Lihat solusinya

Ekspresi

$\left(h \circ g \circ f\right)(x)$

Artinya kita harus menghitung fungsi komposit berikut:

$\left(h \circ g \circ f\right)(x) = h \bigg( g\Big(f(x)\Big) \bigg)$

Jadi pertama-tama kita tentukan

$g\Big( f(x)\Big):$

$\begin{aligned}g\Big( f(x)\Big)&=g\Big(x+1 \Big)\\[2ex]&= 3(x+1)-5\\[2ex]&= 3x+3-5\\[2ex]&= 3x-2\end{aligned}$

Dan sekarang kita menghitung

$h \bigg( g\Big(f(x)\Big) \bigg)$

. Untuk melakukan ini, kami mengganti ekspresi yang ditemukan dari

$g\Big(f(x)\Big)$

di mana muncul

$x$

dalam fungsinya

$h(x):$

$\begin{aligned}h \bigg( g\Big(f(x)\Big) \bigg)&= h \bigg(3x-2\bigg)\\[2ex]&= \sqrt{3x-2} - 3\end{aligned}$

Kita tidak dapat menyederhanakan fungsi komposit lebih jauh lagi. Oleh karena itu, komposisi ketiga fungsi tersebut menghasilkan fungsi yang tidak rasional:

$\bm{\left(h \circ g \circ f\right)(x) =\sqrt{3x-2} - 3 }$

Komposisi fungsi (fungsi gabungan)

Apa itu komposisi fungsi?

Contoh komposisi fungsi

Domain fungsi komposit

Sifat komposisi fungsi

Latihan soal komposisi fungsi

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan