Ketidakpastian tak terhingga dikurangi tak terhingga (∞-∞)

Pada artikel ini kami menjelaskan cara menyelesaikan ketidakpastian tak terhingga dikurangi tak terhingga (∞-∞). Anda akan menemukan contoh ketidakpastian ini dengan berbagai jenis fungsi dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan yang diselesaikan selangkah demi selangkah dari ketidakpastian tak terhingga dikurangi tak terhingga.

Memecahkan ketidakpastian tak terhingga dikurangi tak terhingga

Jika limit suatu fungsi menghasilkan tak terhingga dikurangi tak terhingga, maka itu berarti tak tentu (atau bentuk tak tentu). Artinya , limit suatu fungsi yang memberikan ketidakpastian dikurangi tak terhingga tidak dapat ditentukan dengan melakukan perhitungan langsung, melainkan harus dilakukan prosedur pendahuluan.

Oleh karena itu, untuk menyelesaikan tak hingga dikurangi ketidakpastian tak hingga, pertama-tama kita harus menerapkan prosedur yang bergantung pada jenis fungsinya: jika fungsi polinomial dapat dihitung dengan perbandingan, jika fungsi rasional pecahan harus direduksi menjadi penyebut yang sama, dan jika merupakan fungsi irasional, maka harus dikalikan dengan konjugasinya.

\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty

Selanjutnya, kita akan melihat dengan contoh bagaimana ketidakterbatasan tak terhingga dikurangi tak terhingga diselesaikan dalam setiap jenis fungsi.

Ketidakpastian tak terhingga dikurangi tak terhingga dalam fungsi polinomial

Dalam polinomial, ketidakpastian tak hingga dikurangi tak terhingga sama dengan tak terhingga orde tertinggi, yaitu suku orde tertinggi menentukan tanda positif atau negatif dari tak terhingga.

Misalnya, lihat limit fungsi polinomial berikut yang memberikan bentuk tak terhingga tak terhingga dikurangi tak terhingga:

\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty

Dalam hal ini suku x 2 berpangkat kedua dan suku 3x berpangkat satu, sehingga monomial x 2 dominan karena ordenya lebih tinggi. Oleh karena itu, hasil limitnya adalah tak terhingga yang diperoleh dari suku tersebut.

Lihatlah contoh-contoh lain ini:

\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}

Singkatnya, ketika kita membuat batasan hingga tak terhingga dalam fungsi polinomial , kita harus mengganti tak terhingga ke dalam suku derajat tertinggi , mengabaikan semua suku lainnya.

Ketidakpastian tak terhingga dikurangi tak terhingga dengan pecahan

Ketika ketidakpastian tak terhingga dikurangi tak terhingga terjadi pada penjumlahan atau pengurangan pecahan aljabar , pertama-tama kita harus melakukan penjumlahan atau pengurangan pecahan tersebut lalu menghitung limitnya.

Mari kita lihat cara menghitung tak terhingga tak terhingga dikurangi tak terhingga dalam suatu fungsi pecahan dengan menyelesaikan contoh langkah demi langkah:

\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)

Mari kita coba hitung limitnya dulu:

\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}

Tapi kita mendapatkan ketidakpastian ∞-∞.

Jadi pertama-tama kita perlu melakukan pengurangan pecahan. Untuk melakukan ini, kita mereduksi pecahan menjadi penyebut yang sama, yaitu mengalikan pembilang dan penyebut satu pecahan dengan penyebut pecahan lainnya:

\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}

Dan karena kedua pecahan memiliki penyebut yang sama, kita dapat menggabungkan keduanya menjadi satu pecahan:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}

Kami beroperasi di pembilang dan penyebut:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}

Dan terakhir, kita hitung lagi limitnya:

\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}

Dalam hal ini ketidakterbatasan tak terhingga antara tak terhingga menghasilkan +∞ karena derajat pembilangnya lebih besar daripada derajat penyebutnya.

➤ Lihat: apa itu tak terhingga di antara tak terhingga?

ketidakpastian tak terhingga dikurangi tak terhingga dengan akar-akar

Ketika ketidakpastian tak terhingga dikurangi tak terhingga terjadi pada penjumlahan atau pengurangan radikal , pertama-tama kita harus mengalikan dan membagi fungsi tersebut dengan ekspresi radikal konjugasinya, lalu mencari limitnya.

Kita akan melihat cara menyelesaikan ketidakpastian tak terhingga dikurangi tak terhingga dalam fungsi irasional menggunakan contoh langkah demi langkah:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)

Pertama-tama mari kita coba selesaikan limit fungsi dengan radikal:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}

Namun, kita memperoleh bentuk tak tentu ∞-∞. Jadi, untuk mengetahui berapa besar ketidakpastian yang tak terhingga dikurangi tak terhingga, kita perlu menerapkan prosedur yang telah dijelaskan.

Karena fungsi tersebut memiliki radikal, kita mengalikan dan membagi seluruh fungsi dengan ekspresi irasional terkonjugasi:

\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}

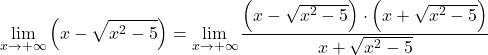
Ekspresi aljabar dari pembilangnya sesuai dengan identitas penting dari hasil kali penjumlahan dengan selisih, oleh karena itu kita dapat menyederhanakan ekspresi tersebut:

\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}

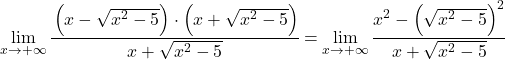
Sekarang kita sederhanakan akar limitnya, karena limitnya dikuadratkan:

\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}

Kami mengoperasikan pembilang pecahan:

\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}

Dan terakhir, kita ulangi perhitungan limitnya:

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}

Oleh karena itu, hasil limitnya adalah 0, karena bilangan apa pun dibagi tak terhingga sama dengan nol.

Memecahkan masalah ketidakpastian tak terhingga dikurangi tak terhingga

Latihan 1

Selesaikan limit berikut ketika x mendekati plus tak terhingga:

\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)

Pada limit ini, suku orde tertinggi adalah derajat ketiga, jadi kita fokus pada tak terhingga yang diperoleh dari suku tersebut.

\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}

Latihan 2

Hitung limit fungsi polinomial berikut ketika x mendekati tak terhingga negatif:

\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)

Negatif tak terhingga pangkat tiga tetap negatif, tetapi bila dikuadratkan menjadi positif. nanti Meskipun tandanya diubah oleh koefisien di depannya:

\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}

Kemudian, bentuk tak terhingga dikurangi tak terhingga didefinisikan oleh suku tertinggi (-5x 3 ), yang darinya kita memperoleh tak terhingga positif:

\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}

Latihan 3

Tentukan limit hingga tak terhingga dari fungsi rasional berikut:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)

Pertama, kita mencoba menghitung limit dengan mengganti fungsi tak terhingga:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}

Namun kita berakhir dengan ketidakpastian ∞ – ∞. Oleh karena itu, kami mereduksi pecahan menjadi penyebut yang sama:

\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}

Dan karena kedua pecahan sekarang memiliki penyebut yang sama, kita dapat menggabungkan keduanya menjadi satu pecahan:

\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}

Kami membuat tanda kurung pada pembilangnya:

\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}

Dan terakhir, kita tentukan batasannya:

\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}

Dalam hal ini ketidakpastian ∞/∞ menghasilkan +∞ karena derajat pembilangnya lebih besar daripada derajat penyebutnya.

Latihan 4

Selesaikan limit fungsi pecahan berikut ketika x mendekati 0:

\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)

Kita coba hitung dulu limitnya seperti biasa:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}

Tapi kita mendapatkan bentuk tak tentu ∞-∞. Oleh karena itu, kita perlu mereduksi pecahan dari fungsi tersebut menjadi penyebut yang sama.

Dalam hal ini, x 4 adalah kelipatan dari x 2 , jadi hanya dengan mengalikan pembilang dan penyebut pecahan kedua dengan x 2 kita akan memperoleh bahwa kedua pecahan tersebut mempunyai penyebut yang sama:

\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}

Sekarang kita dapat mengurangkan kedua pecahan tersebut:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}

Kami mencoba menyelesaikan batasan itu lagi:

\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}

Tapi kita berakhir dengan ketidakpastian suatu konstanta dibagi nol. Oleh karena itu, perlu dihitung batas lateral fungsi tersebut.

\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

Kesimpulannya, karena dua limit lateral fungsi di titik x=0 menghasilkan -∞, maka solusi limitnya adalah -∞:

\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}

Latihan 5

Selesaikan limit hingga tak terhingga dari fungsi berikut dengan akar-akarnya:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)

Mencoba menyelesaikan limitnya, kita memperoleh ketidakpastian tak terhingga dikurangi tak terhingga:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}

Oleh karena itu, karena terdapat radikal dalam fungsi tersebut, kita perlu mengalikan dan membaginya dengan ekspresi radikal terkonjugasi:

\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}

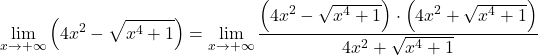
Pada pembilangnya, kita mempunyai hasil kali penting dari suatu penjumlahan dengan selisihnya, yang sama dengan selisih kuadratnya. Belum:

\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}

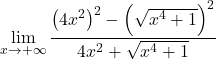
Kita sederhanakan akar ke dalam kuadrat:

\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}

Kami beroperasi di pembilang:

\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}

Dan akhirnya, kami menemukan batasnya:

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}

Dalam hal ini, ketidakterbatasan tak terhingga dibagi tak terhingga menjadi lebih tak terhingga karena derajat pembilangnya lebih besar daripada derajat penyebutnya (ingat bahwa akar kuadrat mengurangi derajatnya menjadi dua:

\sqrt{x^4} = x^{4/2} = x^2

).

Latihan 6

Selesaikan limit ketika x mendekati tak terhingga dari fungsi irasional berikut:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)

Pertama kita coba hitung limitnya seperti biasa:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}

Namun hal ini memberi kita ketidakpastian akan perbedaan ketidakterbatasan. Oleh karena itu, karena fungsi tersebut memiliki akar, kita perlu mengalikan dan membagi ekspresi tersebut dengan radikal terkonjugasi:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}

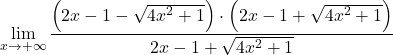
Kami mengelompokkan persamaan penting dari pembilang pecahan:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}

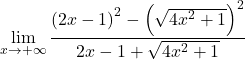
Kami memecahkan akar kuadrat:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Kami memecahkan identitas penting dari kuadrat perbedaan:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Kami beroperasi di pembilang:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}

\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}

Dan terakhir, kita menghitung nilai limit di tak terhingga:

\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =

Meskipun ada x kuadrat pada penyebutnya, namun derajatnya sebenarnya 1 karena berada di dalam akar:

\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .

Oleh karena itu, hasil dari ketidakpastian -∞/+∞ adalah pembagian koefisien x yang berpangkat lebih tinggi, karena pangkat pembilangnya sama dengan pangkat penyebutnya.

\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}

Perhatikan bahwa karena ada dua suku derajat pertama pada penyebutnya

\bigl(2x

Dan

\sqrt{4x^2}\bigr)

, untuk menyelesaikan ketidakpastian -∞/+∞ perlu mengambil semua koefisien suku derajat pertama, yaitu

2

dari

2x

dan itu

\sqrt{4}

dari

\sqrt{4x^2}.

Latihan 7

Hitung limitnya ketika x mendekati 1 fungsi berikut dengan pecahan:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)

Mencoba membuat limitnya, kita mendapatkan limit tak terhingga dari tak terhingga dikurangi tak terhingga:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}

Oleh karena itu, pecahan harus direduksi menjadi penyebut yang sama, atau dengan kata lain, pembilang dan penyebut suatu pecahan harus dikalikan dengan penyebut pecahan lainnya:

\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}

Dan karena kedua pecahan sekarang mempunyai penyebut yang sama, kita dapat menggabungkan keduanya:

\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}

Kami beroperasi:

\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}

\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}

Dan kami mencoba menyelesaikan batasannya lagi:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}

Tapi kita menemukan ketidakpastian nol dibagi nol. Oleh karena itu, kita harus memfaktorkan polinomial pembilang dan penyebutnya:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}

Sekarang kita sederhanakan pecahan dengan menghilangkan faktor yang berulang pada pembilang dan penyebutnya:

\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}

Dan, akhirnya, kami menyelesaikan batasannya:

\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top