Ketidakpastian tak terhingga antara tak terhingga (∞/∞)

Pada artikel ini kami menjelaskan cara menghitung ketidakterbatasan antara ketidakterbatasan (∞/∞). Anda akan menemukan contoh ketidakpastian ini dengan semua jenis fungsi: fungsi polinomial, radikal, eksponensial, dll. Selain itu, Anda akan dapat berlatih dengan latihan yang diselesaikan selangkah demi selangkah dari batasan yang memberikan ketidakpastian tak terhingga di antara ketidakterbatasan.

Bagaimana mengatasi ketidakpastian yang tak terbatas antara yang tak terbatas

Jika limit suatu fungsi menghasilkan tak terhingga dibagi tak terhingga, maka itu berarti tak tentu (atau bentuk tak tentu). Untuk menyelesaikan limit suatu fungsi yang memberikan ketidakterbatasan antara tak terhingga, derajat polinomial pembilangnya harus dibandingkan dengan derajat polinomial penyebutnya.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

Hasil dari ketidakterbatasan tak terhingga dibagi tak terhingga bergantung pada derajat pembilang dan derajat penyebut pecahan:

Jika derajat polinomial pembilangnya lebih kecil dari derajat polinomial penyebutnya, maka ketidakterbatasan dibagi tak terhingga sama dengan nol.
Jika derajat polinomial pembilangnya sama dengan derajat polinomial penyebutnya, maka ketidakpastian tak terhingga terhadap tak terhingga adalah hasil bagi koefisien utama kedua polinomial tersebut.
Jika derajat polinomial pembilangnya lebih besar dari derajat polinomial penyebutnya, maka ketidakterbatasan tak terhingga antara tak terhingga menghasilkan lebih atau kurang tak terhingga (tandanya bergantung pada suku utama kedua polinomial tersebut).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> <h2 class=$ Contoh ketidakpastian tak terhingga antara tak terhingga

Mari kita lihat bagaimana bentuk tak terhingga tak terhingga antar tak terhingga diselesaikan dengan melihat beberapa contoh dari setiap kasus:

derajat pembilangnya lebih kecil dari derajat penyebutnya

Seperti yang kita lihat di atas, jika derajat polinomial pembilangnya lebih kecil dari derajat polinomial penyebutnya, maka limit tak tentu tak terhingga antara tak terhingga selalu menghasilkan 0.

Contoh 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Polinomial pembilangnya berderajat dua, sedangkan penyebutnya berderajat tiga, sehingga penyelesaian limitnya adalah 0.

Contoh 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

Fungsi polinomial pembilangnya berderajat satu, tetapi fungsi penyebutnya berderajat empat, sehingga limit negatif tak terhingga adalah 0.

derajat pembilangnya sama dengan derajat penyebutnya

Bila derajat polinomial pembilangnya sama dengan derajat polinomial penyebutnya, batas tak tentu tak terhingga dengan tak terhingga dihitung dengan membagi koefisien terdepan (koefisien suku derajat lebih tinggi) dari kedua polinomial tersebut.

Contoh 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

Dalam hal ini, kedua polinomial tersebut berderajat kedua, oleh karena itu koefisien suku-suku yang berderajat lebih tinggi perlu dibagi untuk mencari limit pada tak terhingga positif.

Contoh 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

Meskipun limitnya adalah ketika x cenderung minus tak terhingga, ketidakpastian tak terhingga antara tak terhingga diselesaikan dengan cara yang sama.

Derajat pembilangnya lebih besar dari derajat penyebutnya

Jika derajat polinomial pembilangnya lebih besar daripada derajat polinomial penyebutnya, maka bentuk tak terhingga antara tak terhingga akan selalu menghasilkan tak terhingga, dan tanda tak terhingga ditentukan oleh suku-suku derajat yang lebih tinggi dari kedua polinomial tersebut.

Contoh 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Fungsi pembilangnya mempunyai derajat yang lebih tinggi dari pada penyebutnya, sehingga ketidakpastian tak hingga pada tak terhingga menghasilkan tak terhingga. Selain itu, dalam hal ini pembilang dan penyebutnya bernilai positif tak terhingga, sehingga hasil limitnya juga harus positif.

Contoh 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Dalam soal ini, bilangan tak terhingga positif diperoleh dari pembilangnya karena setiap suku kuadrat adalah positif, sebaliknya, bilangan tak terhingga negatif diperoleh dari penyebutnya. Oleh karena itu, batas yang dihasilkan adalah negatif karena positif dibagi negatif sama dengan negatif.

Ketidakpastian tak terhingga antara tak terhingga dengan akar

Kita baru saja melihat cara menghitung ketidakpastian tak terhingga antara tak terhingga jika kita mempunyai fungsi polinomial. Tapi… berapa bilangan tak terhingga dibagi tak terhingga jika kita mempunyai akar?

Derajat suatu fungsi irasional (fungsi yang mempunyai akar) adalah hasil bagi antara derajat suku pokok dan indeks akarnya.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Oleh karena itu, jika limit suatu fungsi yang memiliki akar memberikan ketidakpastian antara tak terhingga , kita harus menerapkan aturan yang sama seperti yang dijelaskan di atas untuk derajat pembilang dan penyebutnya, tetapi dengan mempertimbangkan bahwa derajat polinomial dengan akar dihitung secara berbeda.

Perhatikan contoh limit hingga tak terhingga suatu fungsi dengan radikal berikut ini:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

Pangkat pembilangnya adalah 2 dan pangkatnya adalah 4 (8/2=4), maka limitnya adalah 0 karena pangkat pembilangnya lebih kecil dari pangkat penyebutnya.

Sebaliknya, jika pangkat pembilang dan penyebutnya sama, maka untuk menghitung limit tak tentu, kita harus mengambil koefisien utama dengan akarnya:

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

Ketidakpastian tak terhingga antara tak terhingga dengan fungsi eksponensial

Terakhir, kita hanya perlu mempelajari kasus hasil bagi tak terhingga dari tak terhingga: seberapa besar ketidakterbatasan tak terhingga antara fungsi tak terhingga dan fungsi eksponensial.

Pertumbuhan fungsi eksponensial jauh lebih besar daripada pertumbuhan fungsi polinomial, jadi kita harus memperhitungkan bahwa derajat fungsi eksponensial lebih besar daripada derajat fungsi polinomial.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Oleh karena itu, jika ketidakpastian tak terhingga dibagi tak terhingga dihasilkan dari suatu limit dengan fungsi eksponensial, cukup menerapkan aturan yang sama seperti yang dijelaskan untuk derajat pembilang dan penyebut, tetapi dengan mempertimbangkan bahwa fungsi eksponensial memiliki orde yang lebih tinggi daripada polinomial. . Selain itu, jika kita memiliki fungsi eksponensial pada pembilang dan penyebut pembagian, fungsi eksponensial dengan basis lebih besar akan memiliki orde lebih tinggi. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

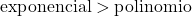
Dalam hal ini penyebutnya dibentuk oleh fungsi eksponensial, sehingga ordenya lebih tinggi dari pembilangnya. Oleh karena itu, bentuk tak terhingga antara tak terhingga lenyap.

Menyelesaikan latihan ketidakpastian tak terhingga antara tak terhingga

Latihan 1

Hitung limit fungsi rasional berikut:

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

lihat solusi

Saat menghitung limit, kita mendapatkan ketidakterbatasan tak terhingga antara tak terhingga, tetapi karena derajat pembilangnya lebih kecil dari derajat penyebutnya, maka batas tak tentu tersebut sama dengan nol.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

Latihan 2

Selesaikan limit tak tentu berikut ini:

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

lihat solusi

Saat mencoba menghitung limit, diperoleh ketidakpastian ∞/∞. Dalam hal ini derajat polinomial pembilangnya lebih besar dari derajat polinomial penyebutnya, sehingga limit tak tentu sama dengan ditambah tak terhingga.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

Latihan 3

Selesaikan limit berikut pada tak terhingga:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

lihat solusi

Batas tersebut memberikan ketidakpastian dikurangi tak terhingga antara plus tak terhingga. Derajat pembilangnya lebih besar dari derajat penyebutnya, sehingga limit tak tentu sama dengan ditambah tak terhingga. Namun, karena pembagian bilangan tak terhingga negatif dengan tak terhingga positif, maka hasilnya adalah minus tak terhingga.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Latihan 4

Selesaikan limit tak tentu berikut ini:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

lihat solusi

Dalam soal ini, bentuk tak tentu tak terhingga terhadap tak terhingga diperoleh dari hasil bagi dua polinomial yang berderajat sama, oleh karena itu, hasil dari batas tak tentu tersebut adalah pembagian koefisien utamanya:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Latihan 5

Hitung batas berikut setidaknya hingga tak terhingga:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

lihat solusi

Derajat ekspresi aljabar pembilangnya lebih kecil dari derajat ekspresi aljabar penyebutnya, sehingga ketidakpastian +∞/+∞ menghasilkan 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Latihan 6

Selesaikan limit tak tentu suatu fungsi berikut dengan akar-akarnya:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

lihat solusi

Pembilangnya berada di bawah akar, sehingga derajatnya adalah 7/3. Sebaliknya, polinomial penyebutnya adalah kuadrat. Dan karena 7/3>2, limitnya menghasilkan plus tak terhingga:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

Latihan 7

Tentukan limit hingga tak terhingga dari fungsi berikut dengan pecahan:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

lihat solusi

Pada latihan kali ini, diperoleh ketidakpastian dikurangi tak terhingga dibagi minus tak terhingga jika derajat pembilangnya lebih besar dari derajat penyebutnya, maka:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Latihan 8

Tentukan limit paling sedikit hingga tak terhingga dari fungsi berikut:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

lihat solusi

Polinomial penyebutnya berbentuk kuadrat, sedangkan polinomial pembilangnya linier. Oleh karena itu, ketidakterbatasan tak terhingga dibagi tak terhingga menghasilkan 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Latihan 9

Selesaikan limit tak terhingga dari fungsi berikut:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

lihat solusi

Pembilangnya lebih besar derajatnya daripada penyebutnya, sehingga hasil dari bentuk tak tentu ∞/∞ tak terhingga. Selain itu, tanda tak terhingga akan menjadi negatif karena bilangan positif dibagi negatif menghasilkan negatif:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Latihan 10

Selesaikan limit berikut dengan ketidakpastian tak terhingga antara tak terhingga:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

lihat solusi

Fungsi eksponensial mempunyai orde yang lebih tinggi daripada fungsi polinomial, sehingga limitnya memberikan tak terhingga. Namun, jika membagi positif dengan negatif, tanda tak terhingga akan menjadi negatif:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Latihan 11

Hitung limit berikut:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

lihat solusi

Dalam soal ini, ketidakterbatasan pada tak terhingga diselesaikan dengan membagi koefisien dominan dari dua polinomial, karena keduanya mempunyai derajat yang sama:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

Latihan 12

Selesaikan limit fungsi berikut ketika x mendekati tak terhingga:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

lihat solusi

Meskipun bilangan yang tidak diketahui pada pembilangnya tidak langsung dikuadratkan, ketika mencari identitas penting kita dapat dengan jelas melihat bahwa derajat pembilangnya lebih besar daripada derajat penyebutnya. Belum:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Latihan 13

Hitung limit hingga tak terhingga dari fungsi berikut dengan akar pangkat tiga:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

lihat solusi

Pembilangnya terdiri dari akar pangkat tiga, jadi derajatnya adalah 3/3=1. Maka derajat pembilangnya sama dengan penyebutnya, sehingga ketidakterbatasan tak terhingga antara tak terhingga diselesaikan sebagai berikut:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

Latihan 14

Selesaikan limit hingga tak terhingga dari fungsi berikut dengan dua radikal:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

lihat solusi

Derajat pembilangnya adalah 7/3 = 2,33 dan derajat penyebutnya adalah 5/2 = 2,5. Oleh karena itu, karena derajat pembilangnya lebih kecil dari derajat penyebutnya, maka batas tak terhingga antara tak terhingga adalah 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Latihan 15

Hitung limit berikut:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

lihat solusi

Terlepas dari derajat pembilangnya, karena kita mempunyai fungsi eksponensial pada penyebutnya, hasil dari bentuk tak terhingga terhadap tak terhingga adalah 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Bagaimana mengatasi ketidakpastian yang tak terbatas antara yang tak terbatas

derajat pembilangnya lebih kecil dari derajat penyebutnya

Contoh 1:

Contoh 2:

derajat pembilangnya sama dengan derajat penyebutnya

Contoh 3:

Contoh 4:

Derajat pembilangnya lebih besar dari derajat penyebutnya

Contoh 5:

Contoh 6:

Ketidakpastian tak terhingga antara tak terhingga dengan akar

Ketidakpastian tak terhingga antara tak terhingga dengan fungsi eksponensial

Menyelesaikan latihan ketidakpastian tak terhingga antara tak terhingga

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Latihan 6

Latihan 7

Latihan 8

Latihan 9

Latihan 10

Latihan 11

Latihan 12

Latihan 13

Latihan 14

Latihan 15

Tinggalkan Komentar Batalkan Balasan