Kemiringan suatu garis (rumus)

Di halaman ini Anda akan menemukan penjelasan paling detail tentang kemiringan suatu garis: apa rumusnya, contoh perhitungannya, apa yang dimaksud dengan konsep kemiringan suatu garis,… Anda juga dapat melihat cara mudah mengidentifikasi kemiringan suatu garis. garis dari persamaannya dan, sebagai tambahan, Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.

Rumus kemiringan suatu garis

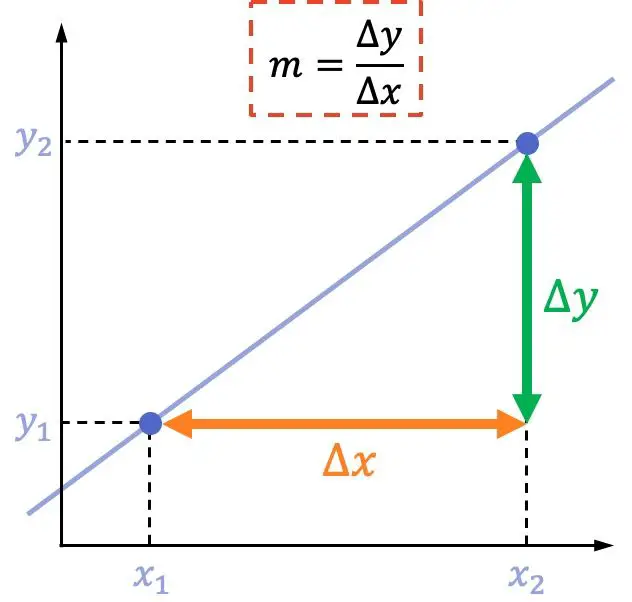
Kemiringan suatu garis sama dengan perpindahan vertikal antara dua titik dibagi dengan perpindahan horizontal antara dua titik yang sama.

Artinya, diberikan dua titik pada sebuah garis:

P_1(x_1,y_1) \qquad P_2(x_2,y_2)

Rumus kemiringan suatu garis adalah:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}

berapa kemiringan suatu garis

Contoh menghitung kemiringan suatu garis dari dua titik

Selanjutnya kita akan melihat contoh cara menghitung kemiringan suatu garis dengan rumus:

  • Hitunglah kemiringan garis yang melalui dua titik berikut:

P_1(3,1) \qquad P_2(5,7)

Untuk mencari kemiringan garis ini, cukup terapkan rumusnya:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}

Oleh karena itu kemiringan garisnya sama dengan 3.

Mencari kemiringan suatu garis dari persamaannya

Pada bagian di atas, kita baru saja melihat cara menentukan kemiringan suatu garis secara numerik. Namun tidak selalu perlu dilakukan perhitungan, tetapi nilainya juga dapat diketahui dari persamaan suatu garis. Setiap jenis persamaan berbeda, jadi kami akan menganalisis setiap kasus secara terpisah.

Kemiringan diberikan persamaan garis yang eksplisit

Persamaan garis eksplisit mengikuti ekspresi berikut:

y =\color{blue}\bm{m}\color{black}x+n

Lalu parameternya

m

sesuai dengan kemiringan garis.

Kemiringan diberikan persamaan titik-kemiringan garis

Rumus persamaan titik-kemiringan garis adalah sebagai berikut:

y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)

Seperti sebelumnya, koefisien

m

sesuai dengan kemiringan garis.

Kemiringan diberikan persamaan garis implisit

Diketahui persamaan garis implisit (disebut juga persamaan umum atau persamaan Cartesius):

Ax+By+C=0

Kemiringan garis dapat dicari dengan melakukan:

m=-\cfrac{A}{B}

Kemiringan dengan memperhatikan vektor arah garis

Vektor arah suatu garis adalah vektor yang menandai arahnya. Jadi, jika vektor arah suatu garis adalah:

\vv{\text{v}}= (\text{v}_1,\text{v}_2)

Kemiringan garis ini adalah:

m=\cfrac{\text{v}_2}{\text{v}_1}

kemiringan yang diberi sudut

Terakhir, jika sebuah garis membentuk sudut

\alpha

pada bagian positif sumbu absis (sumbu X), kemiringannya setara dengan garis singgung sudut:

m = \text{tg}(\alpha)

Arti kemiringan suatu garis

Dengan semua informasi di atas, kita sudah mengetahui betul cara mencari kemiringan suatu garis. Tapi sungguh… apa yang dimaksud dengan kemiringan suatu garis?

Kemiringan suatu garis menunjukkan satuan vertikal yang ditinggikan garis tersebut untuk setiap satuan horizontal grafik.

Misalnya, pada representasi garis berikut, Anda dapat melihat bahwa garis tersebut maju 2 satuan vertikal untuk setiap satuan horizontal, karena kemiringannya sama dengan 2.

berapa kemiringan suatu garis

Selain itu, kemiringan suatu garis juga menunjukkan kecuramannya:

  • Jika suatu garis bertambah (naik), maka kemiringannya positif.
  • Jika suatu garis menurun (menurun), kemiringannya negatif.
  • Jika suatu garis benar-benar horizontal, kemiringannya sama dengan 0.
  • Jika sebuah garis benar-benar vertikal, kemiringannya sama dengan tak terhingga.
kemiringan garis positif atau negatif
kemiringan garis nol atau tak terhingga

Posisi relatif garis

Sebaliknya kedudukan relatif antara dua garis juga dapat diketahui dari sifat-sifat lerengnya:

  • Jika dua garis mempunyai kemiringan yang berbeda, berarti keduanya berpotongan , yaitu berpotongan di suatu titik.
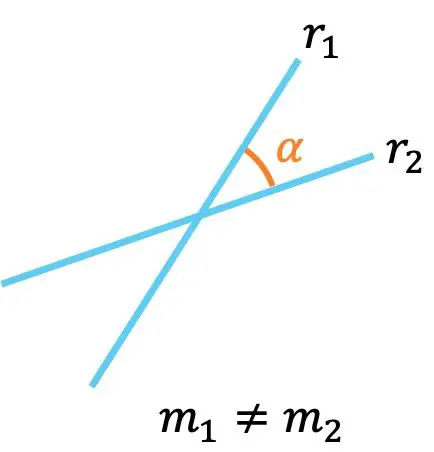
memotong garis lereng yang berbeda

Selain itu, sudut antara dua garis yang melintasi lerengnya dapat dihitung dengan rumus berikut:

\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}

  • Kedua, jika dua garis memiliki kemiringan yang sama, berarti kedua garis tersebut sejajar .
garis sejajar sama kemiringannya
  • Terakhir, kemiringan dua garis tegak lurus atau ortogonal (yang membentuk 90º) memenuhi syarat berikut:
garis tegak lurus terhadap lereng

Ini adalah salah satu cara untuk mengetahui apakah dua garis sejajar atau tegak lurus satu sama lain, namun ada cara lain dan bahkan ada yang lebih cepat. Untuk mengetahui lebih lanjut anda dapat menyimak penjelasan tentang tegak lurus dan paralelisme antar garis . Selain itu, halaman ini juga menjelaskan cara mencari garis yang tegak lurus (atau sejajar) dengan garis lainnya.

Menyelesaikan masalah kemiringan suatu garis

Latihan 1

Tentukan gradien garis yang melalui dua titik berikut:

P_1(5,6) \qquad P_2(8,3)

Untuk menghitung kemiringan garis harus menggunakan rumus:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}

Latihan 2

Hitunglah kemiringan garis yang melalui dua titik berikut:

P_1(-3,1) \qquad P_2(-2,-4)

Untuk mencari kemiringan garis harus menggunakan rumus:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}

Latihan 3

Berapakah kemiringan setiap garisnya?

\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}

A) Garis tersebut dinyatakan sebagai persamaan implisit, sehingga kemiringannya adalah 2 (suku yang menyertainya

x

).

B) Garis ditentukan oleh persamaan titik-kemiringannya, sehingga kemiringannya adalah 4 (angka sebelum tanda kurung).

C) Garis tersebut berbentuk persamaan implisit, sehingga kemiringannya adalah:

m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}

D) Garis didefinisikan dalam bentuk persamaan parametrik, jadi kita harus mencari vektor arahnya terlebih dahulu dan dengan itu kita dapat menghitung kemiringan garis tersebut. Jadi, komponen vektor arah adalah suku-suku yang menyertai koefisien

t:

\vv{\text{v}} = (-1,2)

Dan setelah kita mengetahui vektor arah garis, kita dapat menentukan kemiringan garis:

m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}

Latihan 4

Tentukan kemiringan setiap garis grafik:

persamaan eksplisit latihan garis diselesaikan langkah demi langkah

biru benar

Garis biru bertambah satu Y untuk setiap X, sehingga kemiringannya sama dengan 1.

m=1

hijau kanan

Garis hijau bertambah tiga Y untuk setiap X, jadi kemiringannya adalah 3 .

m=3

garis merah

Garis merah berkurang dua Y untuk setiap X, sehingga kemiringannya sama dengan -2 .

m=-2

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top