Posisi relatif suatu garis dan bidang

Di halaman ini Anda akan menemukan posisi relatif suatu garis dan bidang. Kami menjelaskan kepada Anda bagaimana posisi relatif antara garis dan bidang dihitung (2 metode) dan, sebagai tambahan, Anda akan dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Berapakah kedudukan relatif antara garis dan bidang?

Sebelum melihat semua kemungkinan posisi relatif antara garis dan bidang, kita tentu perlu mengetahui apa itu garis dan bidang . Jadi jika Anda masih belum memahami kedua konsep ini dengan jelas, sebaiknya Anda melihat terlebih dahulu halaman tertaut yang menjelaskannya secara mendetail.

Jadi, dalam geometri analitik, hanya ada tiga posisi relatif dalam ruang antara garis dan bidang:

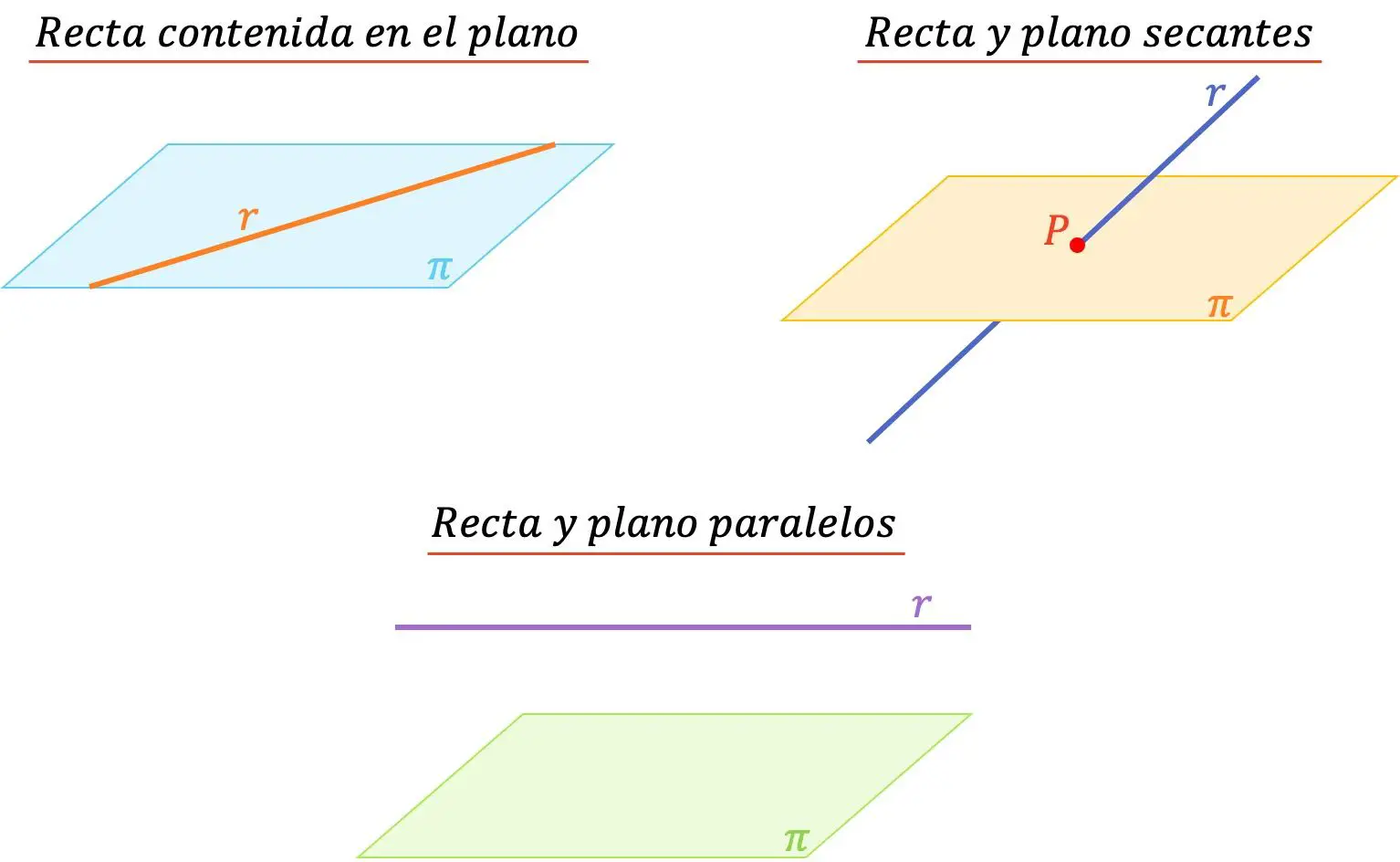
Garis yang terdapat pada bidang : bila garis tersebut terdapat pada bidang, berarti kedua garis tersebut mempunyai titik persekutuan yang jumlahnya tak terhingga.
Garis dan bidang sejajar : Garis dan bidang sejajar jika tidak mempunyai titik yang sama.
Perpotongan garis dan bidang : Garis dan bidang berpotongan jika garis tersebut memotong bidang di suatu titik. Jadi mereka hanya punya satu kesamaan.

Sebaliknya, jika garis berada pada bidang atau sejajar satu sama lain, maka sudut yang dibentuknya adalah 0º. Sebaliknya, ketika garis dan bidang berpotongan, sudut antara kedua elemen geometri dapat berkisar dari 0º (tidak termasuk) hingga 90º (inklusif).

Bagaimana cara menghitung kedudukan relatif suatu garis dan bidang?

Ada dua metode utama untuk mencari posisi relatif antara garis dan bidang dalam ruang: berdasarkan rentang atau vektor .

Jika garis dinyatakan sebagai persamaan implisit (atau umum), akan lebih mudah menggunakan metode rangking. Sebaliknya jika garis diberikan dengan persamaan jenis lain, misalnya berbentuk persamaan vektor, parametrik, atau kontinu, maka lebih cepat menggunakan metode vektor.

Jika Anda tidak ingat seperti apa persamaan garisnya, kami memberikan Anda halaman tempat Anda dapat melihat semua persamaan garis . Di sini Anda akan menemukan semua persamaan garis, rumus untuk menemukan persamaan garis yang melalui dua titik dengan cepat, contoh dan latihan yang diselesaikan langkah demi langkah.

Oleh karena itu, lebih praktis menggunakan satu atau lain cara tergantung masalahnya, untuk itu kami menyarankan Anda mengetahui cara melakukan kedua prosedur tersebut. Di bawah ini adalah penjelasan kedua metode tersebut beserta contohnya.

Ketika garis berbentuk persamaan implisit (atau umum).

Salah satu cara menentukan kedudukan relatif antara suatu garis dan bidang adalah dengan menghitung pangkat dua matriks.

Jika garis ditentukan oleh persamaan implisit (atau umum):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

Dan rencana tersebut juga dinyatakan dalam bentuk persamaan umum:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Kita sebut A sebagai matriks yang terdiri dari koefisien A, B, dan C dari persamaan bidang dan garis:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

Dan matriks A’ akan menjadi matriks yang diperluas dengan semua koefisien dari kedua persamaan:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Kemudian posisi relatif antara garis dan bidang ditentukan oleh nilai luas kedua matriks sebelumnya sesuai tabel berikut:

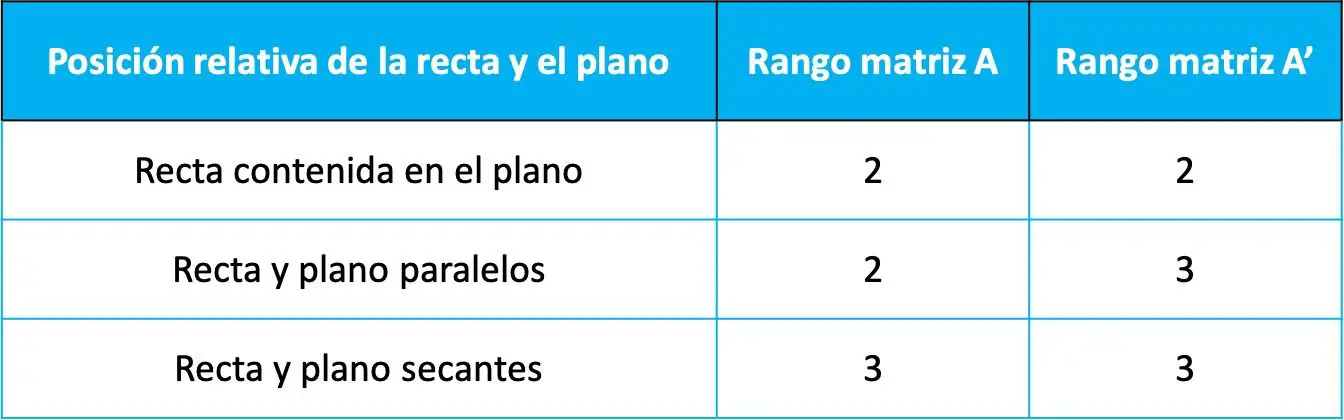
mempelajari posisi relatif antara garis dan bidang dalam ruang berdasarkan jarak

Bahwa posisi relatif bergantung pada pangkat kedua matriks ini dapat ditunjukkan dari toerem Rouche-Frobenius (teorema yang digunakan untuk menyelesaikan sistem persamaan linier). Namun pada halaman ini kami tidak akan melakukan demonstrasi karena tidak perlu diketahui dan juga tidak memberikan banyak manfaat.

Contoh cara mencari posisi relatif suatu garis dan bidang berdasarkan jarak

Agar Anda dapat melihat dengan tepat bagaimana hal ini dilakukan, kami akan menyelesaikan latihan sebagai contoh:

Pelajari kedudukan relatif antara garis berikut dan bidang berikut:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

Garis didefinisikan oleh dua bidang yang berpotongan, sehingga dinyatakan sebagai persamaan implisit. Oleh karena itu, kita akan menggunakan metode rank untuk mempelajari posisi relatif antara garis dan bidang.

Hal pertama yang harus dilakukan adalah membuat matriks A dan matriks perluasan A’ dengan koefisien persamaan:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

Dan sekarang kita perlu menghitung rank masing-masing matriks. Pertama-tama kita mencari luas matriks A dengan determinannya:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

Penentu matriks A adalah nol tetapi mengandung submatriks 2×2 yang determinannya berbeda dengan nol, sehingga merupakan matriks berpangkat 2.

Di sisi lain, perlu juga menghitung rank matriks A’. Dan jangkauan matriks A’ yang diperluas setidaknya akan selalu sama dengan matriks A, jadi kita hanya perlu memeriksa apakah matriks tersebut berpangkat 3 atau 2:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

Sebaliknya, matriks A’ yang diperluas mempunyai subdeterminan 3×3 yang berbeda dari 0, oleh karena itu matriks tersebut berperingkat 3.

Jadi, karena matriks A berpangkat 2 dan matriks A’ berpangkat 3, maka garis dan bidang sejajar .

Ketika garis tersebut berbentuk persamaan jenis lain

Jika garis dinyatakan dengan persamaan selain persamaan implisit, baik persamaan vektor, parametrik, atau kontinu, sebaiknya menggunakan metode yang kami jelaskan di bawah.

Jadi, jika garis diberikan dalam bentuk persamaan vektor, persamaan parametrik, atau persamaan kontinu, berarti kita mengetahui suatu titik yang termasuk dalam garis tersebut dan juga vektor arahnya.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

Di sisi lain, kita juga mengetahui vektor normal (atau tegak lurus) terhadap bidang:

$\vv{n} \perp \pi$

Kemudian dari 2 vektor dan titik garis tersebut dapat dihitung kedudukan relatif antara garis dan bidang sebagai berikut:

Jika hasil kali skalar antara vektor arah garis dan vektor tegak lurus bidang berbeda dari nol, berarti garis tersebut memotong bidang.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
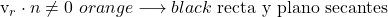
Tetapi jika hasil kali skalar antara vektor arah garis dan vektor tegak lurus bidang sama dengan nol, ada dua kemungkinan: garis tersebut terdapat pada bidang atau sejajar. Dan untuk mengetahui kasusnya, kita harus mensubstitusikan koordinat suatu titik pada garis ke dalam persamaan bidang.
- Jika titik tersebut memenuhi persamaan bidang, maka garis tersebut terdapat pada bidang tersebut.
- Sebaliknya, jika titik tidak memenuhi persamaan bidang, maka garis dan bidang sejajar.

Contoh penentuan kedudukan relatif suatu garis dan bidang dengan menggunakan vektor

Setelah kita melihat teori metode ini, sekarang mari kita lihat latihan yang diselesaikan langkah demi langkah:

Tentukan posisi relatif antara garis berikut dan bidang berikut:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Pertama, garis didefinisikan sebagai persamaan parametrik, sehingga vektor arahnya dan titik yang dilaluinya adalah:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

Dan sebaliknya, vektor normal bidang adalah:

$\vv{n} =(2,1,-2)$

Setelah kita mengetahui vektor arah garis dan vektor tegak lurus bidang, kita harus menghitung hasil kali skalar antara keduanya:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Hasil perkalian titiknya adalah nol, sehingga garis hanya dapat dimuat pada bidang atau sejajar dengannya. Jadi, untuk mengetahui kasusnya, kita substitusikan koordinat kartesius titik pada garis tersebut ke dalam persamaan bidang:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Dengan mensubstitusikan titik garis ke dalam persamaan bidang kita memperoleh persamaan, oleh karena itu titik tersebut menghormati persamaan bidang dan akibatnya garis tersebut termasuk dalam bidang tersebut .