Matriks beraturan atau dapat dibalik

Di halaman ini Anda akan menemukan penjelasan tentang matriks beraturan atau matriks yang dapat dibalik dan cara mengetahui kapan inversi suatu matriks dapat dilakukan dan kapan tidak. Selain itu, Anda juga akan melihat beberapa contoh matriks beraturan untuk memahami konsepnya sepenuhnya dan, terakhir, kami akan menunjukkan kepada Anda semua properti dari jenis matriks ini.

Apa itu matriks beraturan?

Pengertian matriks beraturan adalah sebagai berikut:

Matriks beraturan adalah matriks persegi yang dapat diinversi, yaitu invers dari matriks tersebut dapat dihitung. Oleh karena itu, determinannya bukan nol (0).

Matriks beraturan disebut juga matriks invertible, non-singular, atau non-degenerate .

Matriks yang berlawanan dengan matriks beraturan adalah matriks singular atau matriks degenerasi.

Jadi, untuk mengetahui suatu matriks beraturan atau tunggal, yaitu suatu matriks dapat dibalik atau tidak, cukup dengan menyelesaikan determinan matriks tersebut:

Jika determinan suatu matriks bukan nol, maka matriks tersebut beraturan atau dapat dibalik.

Jika determinan matriks sama dengan nol, maka matriks tersebut berbentuk tunggal atau tidak dapat dibalik.

Kesimpulannya, menghitung determinan suatu matriks adalah cara paling sederhana untuk mengetahui apakah suatu matriks mempunyai invers atau tidak, jadi inilah yang kami rekomendasikan untuk menentukan invertibilitas suatu matriks.

Jika Anda ingin mengetahui cara membalikkan matriks, Anda dapat melihat rumus invers matriks , yang menjelaskan langkah demi langkah cara membalikkan matriks, dan Anda juga akan menemukan beberapa contoh dan latihan penyelesaian untuk dipraktikkan.

Contoh matriks beraturan atau matriks inversi

Setelah kita mengetahui pengertian matriks beraturan atau matriks inversi, mari kita lihat beberapa contoh matriks beraturan yang dimensinya berbeda:

Contoh matriks 2×2 beraturan atau dapat dibalik

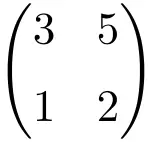
Kita dapat memverifikasi bahwa ini adalah matriks reguler dengan menghitung determinannya:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

Penentu matriks orde 2 berbeda dengan 0, sehingga merupakan matriks beraturan.

Contoh matriks 3×3 beraturan atau dapat dibalik

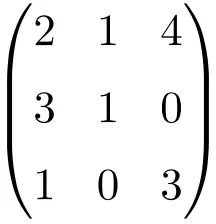
contoh matriks beraturan atau matriks inversi berdimensi 3x3

Kita harus menentukan determinan matriks tersebut untuk membuktikan bahwa matriks tersebut merupakan matriks yang dapat dibalik:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

Penentu matriks orde 3 memberikan hasil selain 0, sehingga merupakan matriks beraturan.

Contoh matriks 4×4 beraturan atau dapat dibalik

contoh matriks beraturan atau matriks inversi berdimensi 4x4

Pengambilan determinan matriks menunjukkan bahwa matriks tersebut merupakan matriks beraturan:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

Penentu matriks berorde 4 tidak nol, sehingga merupakan matriks yang dapat dibalik.

Peringatan: Jika Anda ragu dengan perhitungan determinan, Anda dapat membaca halaman cara menghitung determinan .

Sifat-sifat matriks beraturan atau matriks yang dapat dibalik

Matriks beraturan atau matriks inversi sangat penting untuk aljabar linier, dan hal ini disebabkan oleh ciri-ciri berikut:

Jika A adalah matriks yang dapat dibalik, maka matriksnya juga dapat ditransposisikan atau ditransposisikan. Selain itu, matriks invers transpos sama dengan transpos invers.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

Jangkauan suatu matriks beraturan selalu sebesar mungkin, atau dengan kata lain jangkauan tersebut ekuivalen dengan dimensi matriks.

Hasil kali matriks antara dua matriks yang dapat dibalik menghasilkan matriks beraturan lainnya. Kondisi ini dapat dengan mudah ditunjukkan dengan sifat-sifat determinan:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Setiap matriks ortogonal sekaligus merupakan matriks beraturan.

Misalkan A adalah matriks yang menyatakan sistem persamaan linier
$(Ax=b)$

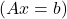
, jika A adalah matriks beraturan, sistem mempunyai solusi unik, oleh karena itu sistem tersebut merupakan sistem determinan yang kompatibel (SCD).

Apalagi jika sistem tersebut merupakan sistem yang homogen
$(Ax=0)$

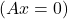
dan A dapat dibalik, penyelesaian sistemnya sepele:

$x=0.$

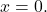
Kolom dan baris matriks beraturan tidak bergantung linier satu sama lain.

Semua nilai eigen (atau nilai eigen) dari matriks beraturan atau matriks yang dapat dibalik adalah bukan nol.

Matriks emas yang dapat dibalik