Halaman ini menjelaskan cara menjumlahkan dua vektor pada bidang, secara grafis dan numerik. Ada 3 cara untuk menjumlahkannya secara grafis: metode jajaran genjang, metode head-to-tail, dan poligon. Selain itu, Anda juga akan menemukan latihan soal penjumlahan vektor dan semua sifat penjumlahan vektor.
Bagaimana cara menjumlahkan dua vektor secara grafis?
Pada dasarnya ada dua cara untuk menjumlahkan vektor dari representasi grafiknya. Dengan kedua bentuk tersebut diperoleh hasil yang sama, namun ada yang lebih suka menjumlahkannya menggunakan metode head-tail dan ada pula yang menggunakan metode jajaran genjang . Oleh karena itu kami akan menjelaskan kedua metode tersebut kepada Anda sehingga Anda dapat memilih salah satu yang Anda sukai. 😉
Sebaliknya kedua cara ini digunakan untuk menjumlahkan dua vektor, namun apa jadinya jika kita ingin menjumlahkan lebih dari dua vektor? Oleh karena itu perlu digunakan metode poligon yang terdiri dari penggunaan metode jajar genjang secara berturut-turut. Anda juga akan menemukan penjelasannya setelah metode head-tail dan parallelogram.
Metode atau aturan jajar genjang
Aturan jajar genjang atau metode jajar genjang (atau hukum jajar genjang) adalah prosedur grafis yang memungkinkan Anda mencari jumlah dua vektor dengan cara yang sangat sederhana. Langkah-langkah yang harus diikuti untuk menerapkan proses ini adalah sebagai berikut:
- Pertama, kita menggambar vektor-vektornya dan menempatkannya pada titik penerapan yang sama, yaitu kita menempatkan asal-usul kedua vektor tersebut pada titik yang sama.
- Kemudian kita menggambar di ujung salah satu vektor sebuah garis yang sejajar dengan vektor lainnya. Dan kami mengulangi langkah tersebut dengan vektor lainnya. Oleh karena itu, kita akan mendapatkan gambar jajar genjang (sesuai dengan nama aturannya).
- Terakhir, hasil penjumlahannya adalah vektor yang bergerak dari titik asal yang sama ke titik perpotongan dua garis sejajar.
Lihatlah contoh umum berikut di mana dua vektor dijumlahkan dengan aturan jajaran genjang:

Hasil penjumlahan vektor-vektor tersebut adalah diagonal jajar genjang yang dibentuknya dengan garis sejajarnya.
metode kepala dan ekor
Metode kepala dan ekor , atau juga dikenal sebagai metode segitiga , adalah prosedur lain yang dapat menjumlahkan dua vektor secara grafis. Dalam hal ini, langkah-langkah yang harus diikuti adalah:
- Pindahkan sebuah vektor yang ditambahkan dan letakkan sehingga titik asal vektor tersebut tepat berada di ujung vektor yang ditambahkan lainnya.
- Hasil penjumlahan vektor adalah ruas yang dimulai dari awal vektor pertama yang ditambahkan ke akhir vektor lainnya. Jika diperhatikan lebih dekat, sebuah segitiga selesai dengan penjumlahan dua vektor dan penjumlahan vektor.
Berikut contoh penjumlahan vektor dengan metode head-to-tail:
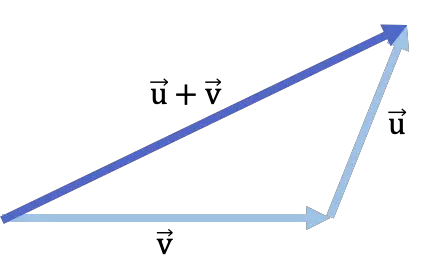
metode poligon
Setelah kita melihat cara menyelesaikan penjumlahan dua vektor secara grafis, kita akan melihat cara menyelesaikannya jika kita mempunyai lebih dari dua vektor.
Saat Anda ingin menjumlahkan tiga vektor atau lebih, ada teknik untuk mempercepat perhitungan operasinya. Teknik ini disebut metode poligon dan terdiri dari penerapan metode head-to-tail secara berturut-turut:
- Pertama-tama kita perlu menempatkan vektor satu demi satu, sehingga titik asal suatu vektor bertepatan dengan ujung vektor lainnya. Urutan penempatannya tidak penting.
- Dan hasil penjumlahannya adalah vektor yang diperoleh dengan menggabungkan awal vektor pertama dengan akhir vektor terakhir.
Perhatikan contoh penjumlahan 4 vektor berikut:
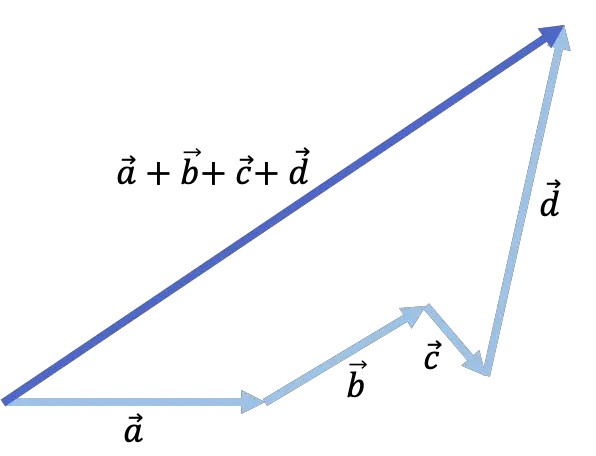
Hitung jumlah dua vektor secara numerik
Setelah kita mengetahui cara menjumlahkan vektor secara geometris, kita akan melihat cara menghitung jumlah vektor secara numerik atau aljabar.
Untuk menjumlahkan dua vektor secara numerik, Anda harus menjumlahkan masing-masing komponennya. Atau dengan kata lain koordinat X kedua vektor tersebut dijumlahkan dan sama dengan koordinat Y.
![]()
![]()
Misalnya penjumlahan antar vektor
![]()
Dan
![]()
Timur:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(1,2) +(5, 3) \\[2ex] & = (1+5,2+3) \\[2ex] & = \bm{(6,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c0813ac0f7ad7fafa1f20b6284430a5_l3.png)
Namun perlu diingat bahwa penjumlahan vektor pada dua buah vektor tidak sama dengan penjumlahan modul vektornya, bahkan hasilnya berbeda total. Anda dapat melihat perbedaan antara kedua operasi tersebut pada sifat-sifat besaran vektor (disebut juga besaran vektor).
Tambahkan Properti Vektor
Penjumlahan vektor mempunyai ciri-ciri sebagai berikut:
- Sifat asosiatif : Menempatkan tanda kurung di antara jumlah beberapa vektor tidak mengubah hasil operasi.
![]()
- Sifat Komutatif – Berbeda dengan pengurangan vektor, hasil penjumlahan antara dua vektor tidak bergantung pada urutan penjumlahannya.
![]()
- Sifat unsur yang berlawanan : jumlah suatu vektor ditambah kebalikannya, yaitu negasinya, sama dengan 0.
![]()
- Properti elemen netral : jelas, vektor apa pun ditambah vektor nol atau nol setara dengan vektor itu sendiri:
![]()
Memecahkan masalah penjumlahan vektor
Latihan 1
Hitung jumlah vektor secara grafis
![]()
Dan
![]()
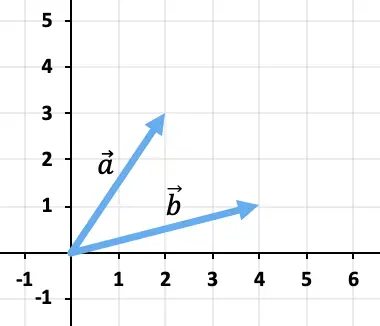
Untuk menjumlahkan kedua vektor tersebut, kita akan menggunakan aturan kepala dan ekor. Oleh karena itu kami akan menempatkan asal vektor
![]()
di akhir vektor
![]()
, dan jumlahnya adalah vektor yang dimulai dari titik asal hingga akhir
![]()
Jadi, hasil penjumlahan vektornya adalah:
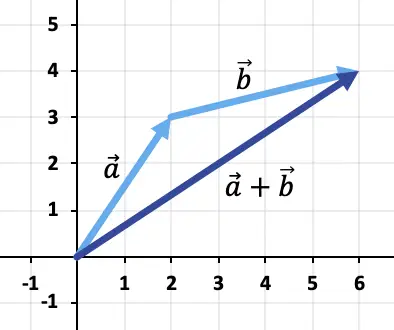
Latihan 2
Selesaikan jumlah vektor secara grafis
![]()
Dan
![]()
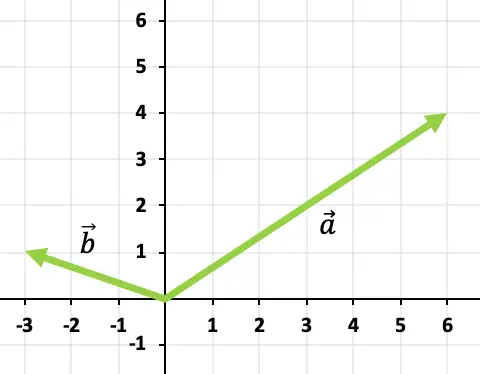
Untuk menjumlahkan kedua vektor, kita akan menggunakan aturan kepala-ekor. Oleh karena itu kami akan menemukan asal muasal vektor
![]()
di akhir vektor
![]()
, dan jumlah vektornya adalah vektor yang dimulai dari titik asal sumbu hingga akhir
![]()
Jadi, hasil penjumlahan vektornya adalah:
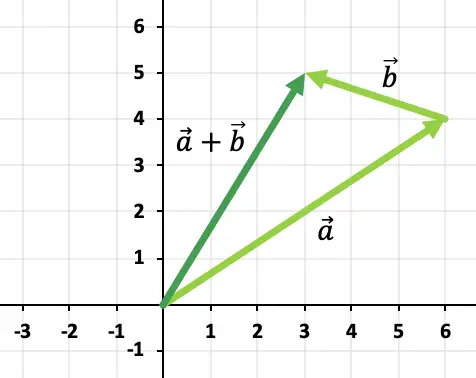
Latihan 3
Tentukan secara grafis vektor yang dihasilkan dari penjumlahan semua vektor yang direpresentasikan dalam grafik:
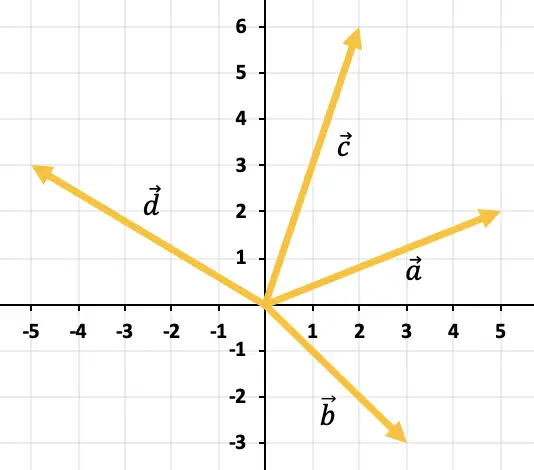
Untuk menjumlahkan lebih dari 2 vektor dari grafik, Anda harus menggunakan aturan poligon. Oleh karena itu kita harus memindahkan vektor-vektor tersebut agar tetap kontinu, yaitu satu demi satu (urutan tidak relevan). Jadi jumlah seluruh vektor adalah vektor yang dimulai dari titik asal vektor pertama sampai ke ujung vektor terakhir.
Jadi hasil penjumlahan keempat vektor tersebut adalah vektor yang dilambangkan dengan warna merah:
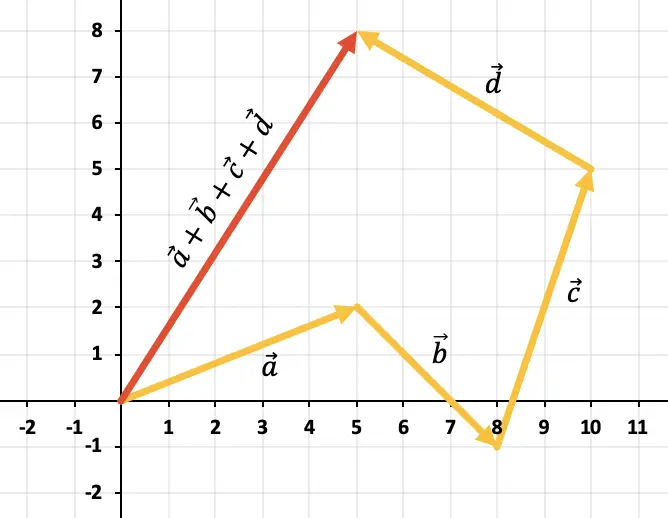
Latihan 4
Temukan secara numerik jumlah vektor-vektor berikut:
![]()
Untuk menjumlahkan dua vektor secara numerik, Anda harus menjumlahkan koordinatnya masing-masing:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}& =(3,-2)+(-4,6) \\[2ex] & = (3+(-4) ,-2+6)\\[2ex] & =\bm{(-1,4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6299484debe49023b686839df40f88b_l3.png)
Latihan 5
Hitung secara analitis jumlah vektor-vektor berikut:
![]()
Untuk menjumlahkan vektor secara numerik, Anda harus menjumlahkan koordinatnya masing-masing:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}+\vv{c}+\vv{d}& =(-1,3)+(4,0)+(2,-5)+(3,-2) \\[2ex] & = (3,3)+(2,-5)+(3,-2) \\[2ex] & = (5,-2)+(3,-2)\\[2ex] & =\bm{(8,-4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05b7c1606bfa3d94d080163a40dc4412_l3.png)