Jarak dari suatu titik ke bidang dalam ruang (rumus)

Di halaman ini Anda akan mengetahui cara menghitung jarak antara suatu titik dan bidang dalam ruang (rumus). Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan yang diselesaikan langkah demi langkah.

Berapa jarak suatu titik ke bidang?

Dalam geometri analitik, jarak suatu titik ke suatu bidang adalah jarak terpendek antara suatu titik dan titik lain pada bidang tersebut. Jarak ini sama dengan panjang ruas yang tegak lurus bidang yang bergerak dari titik ke bidang.

Rumus jarak suatu titik ke bidang

Setelah kita melihat secara pasti pengertian jarak antara suatu titik dan bidang, sekarang mari kita lihat rumus untuk menghitung jarak tersebut:

Diberikan sebuah titik dan persamaan umum (atau implisit) sebuah bidang:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

Rumus jarak suatu titik ke bidang adalah:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Pembuktian rumus jarak suatu titik ke bidang cukup melelahkan dan panjang, sehingga tidak akan kami lakukan di halaman ini.

Sebaliknya, jika pada saat menerapkan rumus kita memperoleh hasil yang sama dengan nol, berarti jarak antara titik dan bidang adalah nol, sehingga titik tersebut merupakan bagian dari bidang tersebut.

Terakhir, perhatikan bahwa untuk menerapkan rumus tersebut, rencana tersebut harus didefinisikan sebagai persamaan umum (atau implisit). Jadi, jika persamaan tersebut dinyatakan dengan persamaan bidang jenis lain, pertama-tama kita harus mengubahnya menjadi persamaan umum lalu menggunakan rumusnya.

Contoh penghitungan jarak suatu titik ke bidang

Agar Anda dapat melihat bagaimana jarak antara suatu titik dan bidang ditentukan secara numerik, kita akan menyelesaikan contoh di bawah ini:

Hitung jarak antara titik P dan bidang π. Karena itu poin dan rencana:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Untuk mencari jarak dari suatu titik ke bidang, cukup terapkan rumus yang terlihat pada bagian di atas:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Sekarang kita substitusikan nilai setiap yang tidak diketahui ke dalam rumus:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

Dan terakhir, kami melakukan operasi:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Perhatikan bahwa pada pembilang pecahan terdapat nilai mutlak dan pada penyebutnya kita mempunyai akar kuadrat, sehingga hasilnya harus selalu positif. Hal ini masuk akal karena jarak tidak bisa bernilai negatif, namun selalu positif.

Hitung jarak antara dua bidang sejajar

Dua bidang sejajar selalu berjarak sama, oleh karena itu untuk mencari jarak antara dua bidang sejajar, kita dapat mengambil sebuah titik pada salah satu bidang tersebut dan menghitung jarak dari titik tersebut ke bidang lainnya.

Ini adalah metode untuk mencari jarak antara dua bidang sejajar. Namun, ada cara yang lebih sederhana untuk melakukan hal ini ketika koefisien A, B, dan C dari persamaan kedua bidang bertepatan:

Perhatikan persamaan umum (atau implisit) dari dua bidang sejajar:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

Rumus untuk menghitung jarak antara dua bidang sejajar adalah:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

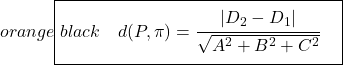
Jadi pastinya lebih mudah mencari jarak antara dua bidang sejajar dengan menggunakan rumus tersebut karena tinggal menerapkan rumusnya saja, tapi tergantung soal. Selain itu, menurut kami yang terbaik adalah menjelaskan kedua cara menghitung jarak sehingga Anda dapat memilih salah satu yang Anda sukai.

Contoh penghitungan jarak antara dua bidang sejajar

Sebagai contoh, kita akan menghitung jarak antara dua bidang berikut:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Pertama-tama kita harus memverifikasi bahwa kita berhadapan dengan dua bidang paralel. Jadi, semua koefisien persamaan bidang adalah proporsional kecuali suku-suku bebasnya, sehingga keduanya merupakan dua bidang sejajar.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Dalam hal ini, suku A, B, dan C persamaan kedua bidang tidak berhimpitan, tetapi kita dapat mencapainya dengan membagi seluruh persamaan bidang kedua dengan dua:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Jadi persamaan kedua bidang tersebut sudah mempunyai koefisien A, B dan C yang sama. Oleh karena itu, kita dapat dengan mudah menghitung jarak kedua bidang tersebut dengan rumus jarak antara dua bidang sejajar:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Kami mengganti nilainya dan menyelesaikan operasi:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Sehingga jarak antara satu bidang dengan bidang lainnya sama dengan satu kesatuan.

Menyelesaikan masalah jarak dari suatu titik ke bidang

Latihan 1

Hitung jarak antara titik P dan bidang yang persamaan kartesiusnya (atau umum) adalah:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

lihat solusi

Untuk menghitung jarak dari suatu titik ke bidang, Anda harus menggunakan rumus yang sesuai:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Kami mengganti nilai setiap parameter ke dalam rumus:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

Dan terakhir, kami melakukan operasi:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Latihan 2

Tentukan jarak antara titik P dan bidang π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

lihat solusi

Sebelum menggunakan rumus jarak suatu titik ke bidang, terlebih dahulu kita harus menyatakan bidang tersebut dalam bentuk persamaan implisit (atau umum):

$\pi: \ -5x+y+2z=0$

Dan sekarang kita bisa menggunakan rumus untuk menentukan jarak dari suatu titik ke bidang:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Kami mengganti nilai setiap suku ke dalam rumus:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

Dan terakhir, kami melakukan operasi:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Latihan 3

Gunakan rumus jarak antara titik dan bidang untuk menentukan apakah titik P terletak pada bidang π.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

lihat solusi

Untuk mengecek apakah suatu titik termasuk dalam bidang, kita dapat menghitung jarak antara keduanya: jika jaraknya nol berarti titik tersebut memang termasuk dalam bidang, sebaliknya jika jaraknya berbeda dari 0 berarti titik tersebut memang milik bidang. titiknya berada di luar pesawat. rencana.

Oleh karena itu, kita menentukan jarak antara titik dan bidang dengan rumus:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

Jarak antara suatu titik dan bidang sama dengan nol, sehingga secara efektif titik tersebut termasuk dalam bidang tersebut.

Latihan 4

Tentukan jarak antara dua bidang berikut:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

lihat solusi

Pertama-tama kita harus memverifikasi bahwa kita berhadapan dengan dua bidang paralel. Semua koefisien persamaan kedua bidang adalah proporsional, kecuali suku-suku bebasnya, jadi kedua bidang tersebut memang sejajar.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Dalam hal ini, kita akan menghitung jarak antara dua bidang dengan rumus, karena koefisien A, B, dan C sama:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Jadi, kami mengganti nilainya ke dalam rumus dan melakukan operasi:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Latihan 5

Tentukan jarak antara dua bidang sejajar berikut:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

lihat solusi

Bidang latar depan didefinisikan dalam bentuk persamaan parametrik, sehingga untuk menerapkan rumus jarak antara dua bidang sejajar kita harus mengubahnya terlebih dahulu ke dalam bentuk persamaan umum dan memerlukan banyak perhitungan dan waktu. Oleh karena itu, akan lebih cepat jika kita mengambil suatu titik pada bidang tersebut dan menghitung jarak dari titik tersebut ke bidang lainnya.

Jadi, koordinat titik yang dilalui bidang π ₁ sesuai dengan suku-suku independen dari setiap persamaan parametrik:

$P(3,-2,5)$