Pada artikel ini kami menjelaskan apa itu ketidakpastian. Anda akan mengetahui apa saja jenis ketidakpastian dan cara mengatasinya. Selain itu, Anda akan dapat melihat latihan yang diselesaikan selangkah demi selangkah pada batas fungsi semua ketidakpastian.
Apa itu ketidakpastian?
Tak tentu, disebut juga bentuk tak tentu, adalah ekspresi matematika yang muncul dalam penghitungan limit fungsi yang hasilnya tidak terdefinisi. Oleh karena itu, untuk menyelesaikan masalah ketidakpastian limit tersebut, perlu diterapkan prosedur pendahuluan yang bergantung pada jenis fungsinya.
Artinya, ketika kita mendapatkan ketidakpastian, bukan berarti limitnya tidak ada atau tidak bisa diselesaikan, melainkan kita harus melakukan perubahan pada fungsi tersebut untuk menemukan solusi dari limit tersebut.
Jenis-jenis ketidakpastian
Bentuk tak tentu, atau bentuk tak tentu, diklasifikasikan ke dalam jenis berikut:
- Ketidakpastian tak terhingga dikurangi tak terhingga (∞-∞)
- Jumlah ketidakpastian antara nol (k/∞)
- Nol ketidakpastian antara nol (0/0)
- Ketidakpastian tak terhingga antara tak terhingga (∞/∞)
- Ketidakpastian 1 dinaikkan hingga tak terhingga (1 ∞ )
- Nol ketidakpastian dinaikkan menjadi nol (0 0 )
- Nol ketidakpastian untuk tak terhingga (0·∞)
- Ketidakpastian nol dinaikkan hingga tak terhingga (0 ∞ )
- Ketidakpastian tak terhingga menjadi nol (∞ 0 )
Kita kemudian akan melihat bagaimana menyelesaikan semua jenis ketidakpastian.
Ketidakterbatasan dikurangi ketidakpastian yang tidak terbatas
Bentuk tak terhingga dikurangi tak terhingga tidak sama dengan nol, karena kita mengurangkan dua bilangan yang sangat besar tetapi kita tidak mengetahui mana yang lebih besar. Oleh karena itu, hasil selisih tak terhingga bergantung pada orde tiap tak terhingga.
Menyelesaikan ketidakpastian jenis ini tidaklah mudah, karena bergantung pada jenis fungsinya, satu prosedur atau lainnya harus diterapkan. Oleh karena itu, kami menyarankan Anda melihat penjelasan lengkapnya pada link berikut:
➤ Lihat: cara menyelesaikan ketidakpastian tak terhingga dikurangi tak terhingga
Jumlah ketidakpastian antara nol
Ketidakpastian suatu konstanta dibagi nol diperoleh dengan menghilangkan penyebut suatu fungsi rasional.
Hasil bentuk tak tentu jenis ini akan selalu lebih tak terhingga, kurang tak terhingga, atau limit fungsinya tidak akan ada. Mari kita lihat bagaimana ketidakpastian ini dihitung dengan menyelesaikan suatu limit sebagai contoh:
Kita telah memperoleh ketidakpastian suatu bilangan dibagi nol, jadi kita perlu menghitung batas lateral fungsi tersebut:
➤ Lihat: apa yang dimaksud dengan batas lateral?
Kedua limit lateral fungsi tersebut memberikan hasil yang sama, jadi menurut definisi limit fungsi ketika x cenderung ke 0 menghasilkan minus tak terhingga:
Perhatikan bahwa jika batas lateral memberikan nilai yang berbeda, batas fungsi pada titik ini tidak akan ada.
Nol antara nol ketidakpastian
Batas tak tentu nol dibagi nol sangat umum dan diperoleh dalam fungsi pecahan yang pembilang dan penyebutnya hilang.
Jenis batas tak tentu ini diselesaikan secara berbeda bergantung pada fungsinya. Misalnya, jika suatu fungsi memiliki akar, langkah-langkah berbeda harus dilakukan. Anda dapat melihat berbagai penyelesaian dari jenis ketidakpastian ini di tautan berikut:
➤ Lihat: cara mengatasi ketidakpastian nol antara nol
Ketidakpastian yang tak terbatas antara yang tak terbatas
Ketidakpastian tak terhingga antara tak terhingga biasanya terjadi pada batas tak terhingga fungsi dengan pecahan. Walaupun ketidakpastian adalah hasil bagi dari dua ketidakterbatasan, hasilnya tidak harus selalu tak terhingga.
Jenis bentuk tak tentu ini diselesaikan dengan perbandingan. Artinya, derajat pembilang dan derajat penyebutnya diamati dan, bergantung pada mana yang lebih besar, hasil batasnya adalah salah satu atau yang lainnya. Anda dapat melihat semua kasus di tautan berikut:
➤ Lihat: menyelesaikan latihan pada batas tak terhingga antara tak terhingga
Ketidakpastian 1 dinaikkan hingga tak terhingga
Secara matematis, seseorang mungkin berpikir bahwa 1 hingga tak terhingga menghasilkan 1, karena pangkat apa pun dari 1 sama dengan 1. Namun, suku ini merupakan suatu ketidakpastian dan, oleh karena itu, seseorang tidak dapat menyimpulkan hasilnya dengan mudah.
Jenis ketidakpastian ini dihitung dengan menggunakan rumus berikut:
![\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6bc13731241df168c3dc37d3e3b8e58_l3.png "Rendered by QuickLaTeX.com")
Misalnya, limit berikut ini tidak dapat ditentukan karena memberikan pangkat tak terhingga:
Oleh karena itu kita harus menggunakan rumus untuk jenis ketidakpastian ini:
![\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e577daa5f0e768ca16bfe27a4d7a8a85_l3.png "Rendered by QuickLaTeX.com")
Jadi kita telah menyelesaikan batas tak tentu yang dinaikkan hingga tak terhingga.
Nol ketidakpastian dibawa ke nol
Ketidakpastian nol terhadap pangkat nol muncul dalam batas-batas fungsi yang rumit.
Untuk mengatasi jenis batas tak tentu ini, Anda harus menggunakan properti batas berikut:
Misalnya, limit berikut memberikan bentuk tak tentu 0 pangkat 0:
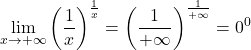
Tetapi jika kita menerapkan logaritma pada limitnya, kita dapat menemukan nilainya:
![\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04165b15f4b40bbe84ae5a4b214d4846_l3.png "Rendered by QuickLaTeX.com")
Nol ketidakpastian untuk ketidakterbatasan
Sulit untuk menemukan ketidakpastian hasil kali nol dan tak terhingga , namun bukan berarti mudah untuk menentukannya.
Tidak ada metode tunggal untuk menyelesaikan jenis ketidakpastian ini, namun hal ini bergantung pada jenis fungsinya. Dalam hal ini, kita harus mengubah fungsinya menjadi ketidakpastian tak terhingga dibagi tak terhingga atau ketidakpastian nol dibagi nol, dan dari sana terapkan metode solusi yang kita lihat di atas untuk setiap ketidakpastian.
Jadi jika limit suatu fungsi adalah 0 dan limit fungsi lainnya adalah ∞:
Kita dapat mengubah tipe ini tanpa batas waktu dengan melakukan perubahan berikut:
![\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df402461269ae26c30768fc0bf83f2ea_l3.png "Rendered by QuickLaTeX.com")
Mari kita lihat cara melakukannya dengan menyelesaikan limit tak tentu sebagai contoh:
Kita operasikan fungsi tersebut untuk memperoleh ketidakpastian tak terhingga terhadap tak terhingga, lalu kita cari limitnya:
![\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c29bbb439514449cd12fd8d66e327af_l3.png "Rendered by QuickLaTeX.com")
Ketidakpastian nol dinaikkan hingga tak terhingga
Ketidakpastian angka nol yang dipangkatkan hingga tak terhingga agak sulit untuk dipahami, karena kita menaikkan angka yang sangat kecil menjadi angka yang sangat besar.
Bila diperoleh bentuk tak tentu ini, rumus berikut harus digunakan:
Mari kita selesaikan sebuah contoh untuk lebih memahami cara menghitung jenis ketidakpastian ini:
![\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ca354428ea8889a956a9b77b04a088f_l3.png "Rendered by QuickLaTeX.com")
Ketidakpastian yang tak terbatas menjadi nol
Biasanya, pangkat apa pun yang dipangkatkan ke nol menghasilkan 1, namun, ketidakpastian tak terhingga yang dipangkatkan ke nol tidak harus selalu seperti ini.
Seperti pada bilangan tak tentu, nol dipangkatkan menjadi nol dan nol dipangkatkan hingga tak terhingga, untuk menyelesaikan jenis batas tak tentu ini perlu diterapkan logaritma:
Mari kita lihat bagaimana jenis limit tak tentu ini diselesaikan dengan menghitung contoh langkah demi langkah:
![\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a45090015a206189aca3884f8b2cab30_l3.png "Rendered by QuickLaTeX.com")