Di halaman ini Anda akan menemukan penjelasan tentang apa itu bidang, cara menghitungnya, dan segala propertinya. Selain itu, Anda juga dapat melihat contoh bidang, posisi relatif antara dua bidang, cara menentukan sudut antara 2 bidang, dan terakhir, cara menyatakan bidang secara numerik menggunakan persamaan bidang.
Apa itu rencana?
Dalam geometri analitik, pengertian bidang adalah sebagai berikut:
Bidang adalah suatu benda geometri yang mempunyai dua dimensi (panjang dan lebar).
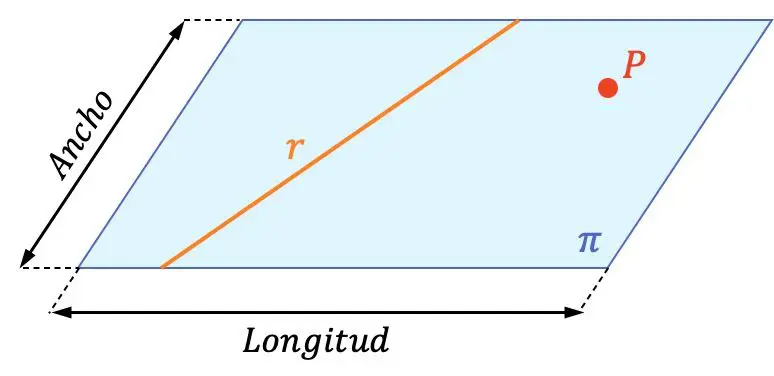
Oleh karena itu, sebuah bidang memuat garis-garis tak terhingga dan titik-titik tak terhingga. Pada representasi grafis di atas Anda dapat melihat perbedaan antara bidang, garis, dan titik. Anda juga dapat memverifikasi garis itu
![]()
dan ujungnya
![]()
terkandung di dalam pesawat
![]()
Seperti yang Anda lihat pada grafik denah, denah biasanya diberi nama dengan huruf Yunani:
![]()
Contoh bidang yang banyak kita gunakan dalam matematika adalah bidang Cartesian. Bidang Kartesius adalah bidang yang ditentukan oleh sumbu absis (sumbu X) dan sumbu ordinat (sumbu Y). Salah satu kegunaan bidang kartesius adalah untuk menggambarkan kedudukan suatu benda dalam suatu sistem acuan.
Menentukan rencana
Sekarang kita telah melihat arti sebuah bidang, mari kita lihat bagaimana bidang apa pun dalam ruang tiga dimensi (dalam R3) dapat ditentukan.
Suatu denah seluruhnya ditentukan oleh unsur-unsur geometri berikut:
- Tiga poin tidak selaras.
- Garis lurus dan titik di luar.
- Dua garis sejajar atau dua garis berpotongan.
Mengenai poin terakhir, Anda mungkin sudah tahu apa yang dimaksud dengan dua garis sejajar. Namun pengertian garis potong kurang diketahui, jadi jika Anda memiliki pertanyaan di sini, Anda dapat melihat apa itu garis potong .
Oleh karena itu, jika kita memiliki salah satu dari 3 syarat sebelumnya, berarti kita bisa membuat rencana.
properti rencana
Rencana tersebut memenuhi karakteristik berikut:
- Sebuah bidang berisi titik-titik yang tak terhingga.
- Sebuah bidang berisi garis-garis yang tak terhingga.
- Sebuah bidang tidak terbatas, yaitu permukaan yang memanjang dalam ruang tanpa batas.
- Dua bidang yang berpotongan menentukan suatu garis.
- Garis yang mempunyai titik pada suatu bidang belum tentu terdapat di sana. Agar sebuah garis dapat menjadi bagian dari suatu bidang, garis tersebut harus mempunyai paling sedikit dua titik pada bidang tersebut.
- Bidang tak terhingga melintasi garis lurus.
- Setengah bidang adalah masing-masing dari 2 bagian yang membagi bidang bila dipotong oleh salah satu garisnya.
persamaan bidang
Dalam geometri analitik, persamaan bidang adalah persamaan yang memungkinkan bidang apa pun dinyatakan secara matematis. Jadi, untuk mencari persamaan suatu bidang, Anda hanya memerlukan sebuah titik dan dua vektor bebas linier yang dimiliki bidang tersebut.

Namun seperti yang telah kita lihat pada penjelasan konsep denah di atas, ada beberapa cara untuk menentukan denah. Dengan cara yang sama, ada juga cara berbeda untuk mengungkapkan rencana secara analitis.
Jadi semua jenis persamaan bidang adalah: persamaan vektor , persamaan parametrik , persamaan implisit (atau umum) , dan persamaan bidang kanonik (atau segmental) .
Selanjutnya kita akan melihat secara detail penjelasan dan rumus semua persamaan denahnya.
Persamaan vektor bidang
Perhatikan sebuah titik dan dua vektor arah pada sebuah bidang:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Rumus persamaan vektor suatu bidang adalah:
![]()
Atau setara:
![]()
Emas
![]()
Dan
![]()
adalah dua skalar, yaitu dua bilangan real.
Persamaan parametrik bidang
Rumus persamaan parametrik suatu bidang adalah:
![]()
Emas:
-
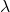
Dan
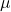
adalah dua skalar, yaitu dua bilangan real.
-
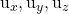
adalah komponen dari salah satu dari dua vektor pemandu denah tersebut
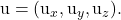
-
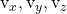
adalah komponen vektor pengarah denah lainnya
Persamaan bidang implisit atau umum
Perhatikan sebuah titik dan dua vektor arah pada sebuah bidang:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Persamaan implisit, umum, atau Cartesian suatu bidang diperoleh dengan menyelesaikan determinan berikut dan menetapkan hasilnya sama dengan 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Dengan demikian, persamaan implisit atau umum dari rencana yang dihasilkan adalah sebagai berikut:
![]()
Persamaan bidang jenis ini disebut juga persamaan bidang kartesius.
Persamaan bidang kanonik atau segmental
Rumus persamaan kanonik atau segmental suatu bidang adalah sebagai berikut:
![]()
Emas:
-

adalah titik potong antara bidang dan sumbu X.
-

adalah titik potong antara bidang dan sumbu Y.
-

Di sinilah bidang memotong sumbu Z.
Persamaan kanonik (atau persamaan segmental) bidang juga dapat diperoleh dari persamaan umumnya:
![]()
Pertama, kita selesaikan koefisien D dari persamaan:
![]()
Kemudian kita membagi seluruh persamaan denah dengan nilai parameter D yang diubah tandanya:
![]()
![]()
Dan, dengan menggunakan sifat-sifat pecahan, kita sampai pada ekspresi berikut:
![]()
Oleh karena itu, dari ungkapan ini kami menyimpulkan rumus yang memungkinkan suku-suku persamaan kanonik atau segmental suatu bidang dihitung secara langsung:
![]()
Oleh karena itu, untuk dapat membentuk varian persamaan denah tersebut, koefisien A, B, dan C harus berbeda dari nol, sehingga menghindari ketidakpastian pecahan.
Posisi relatif dua bidang
Dalam geometri analitik, hanya ada tiga kemungkinan posisi relatif antara dua bidang: bidang potong, bidang sejajar, dan bidang berimpit.
- Bidang berpotongan : Dua bidang berpotongan jika hanya berpotongan pada satu garis.
- Bidang sejajar : Dua bidang sejajar jika tidak berpotongan di titik mana pun.
- Bidang-bidang yang bersinggungan : Dua bidang dikatakan berhimpitan jika kedua bidang tersebut mempunyai titik-titik yang sama.
pesawat yang berpotongan

bidang paralel

pesawat yang kebetulan

Selain itu, jika dua bidang yang berpotongan berpotongan dengan sudut 90º, keduanya merupakan dua bidang yang saling tegak lurus .
Sudut antara dua bidang
Sudut antara dua bidang sama dengan sudut yang dibentuk oleh vektor-vektor normal bidang tersebut. Oleh karena itu, untuk mencari sudut antara dua bidang, dihitung sudut yang dibentuk oleh vektor-vektor normalnya, karena keduanya ekuivalen.
Nah, setelah kita mengetahui secara pasti apa yang dimaksud dengan sudut antara dua bidang, mari kita lihat rumus menghitung sudut antara dua bidang dalam ruang, yang diturunkan dari rumus sudut antara dua vektor:
Mengingat persamaan umum (atau implisit) dari dua bidang berbeda:
![]()
![]()
Vektor normal setiap bidang adalah:
![]()
![]()
Dan sudut yang dibentuk oleh kedua bidang tersebut ditentukan dengan menghitung sudut yang dibentuk oleh vektor-vektor normalnya dengan menggunakan rumus sebagai berikut:
![]()
Tentunya, setelah kita menghitung kosinus sudut yang dibentuk oleh kedua bidang dari rumus tersebut, kita harus membalikkan kosinus tersebut untuk mencari nilai sudut tersebut.
Sebaliknya jika kedua bidang tegak lurus atau sejajar maka rumus tersebut tidak perlu diterapkan, karena sudut antara kedua bidang tersebut dapat ditentukan secara langsung:
- Sudut antara dua bidang sejajar adalah 0º, karena vektor-vektor normalnya mempunyai arah yang sama.
- Sudut antara dua bidang yang tegak lurus adalah 90º, karena vektor-vektor normalnya juga tegak lurus (atau ortogonal) satu sama lain sehingga membentuk sudut siku-siku.