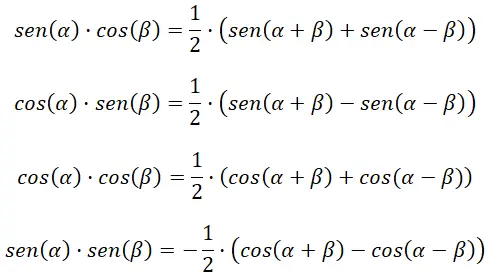Identitas trigonometri adalah persamaan antara fungsi trigonometri yang berbeda. Berkat persamaan trigonometri ini, kita dapat menyimpulkan rasio trigonometri tertentu berdasarkan rasio trigonometri lainnya. Oleh karena itu, perlu diketahui rumus perbandingan tersebut agar dapat memahami rumus identitas trigonometri. Jika Anda tidak mengetahuinya dalam kasus Anda, kami menyarankan Anda mengunjungi tautan terakhir.
Tabel identitas trigonometri
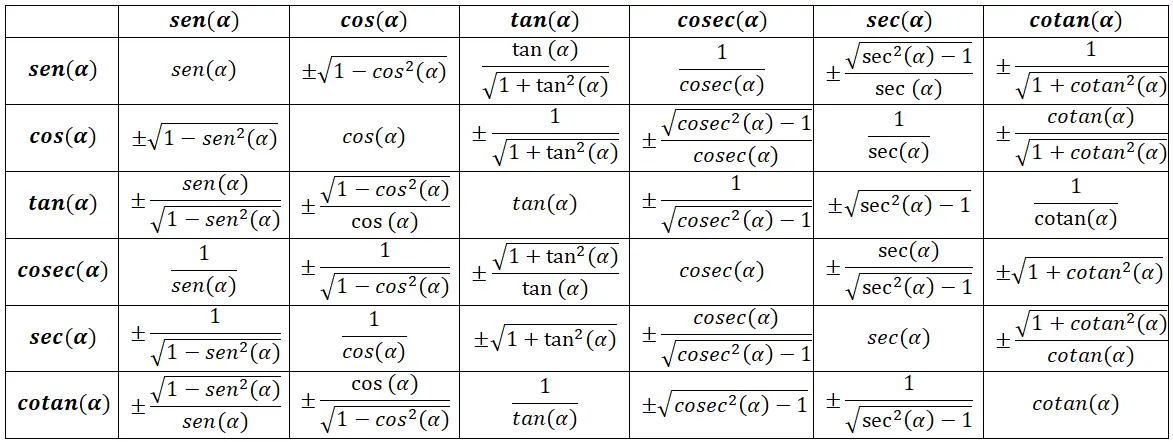
Identitas trigonometri dasar
Ada sederet identitas trigonometri dasar yang dianggap paling penting karena memberikan landasan teori bagi yang lain. Ini adalah yang paling umum ditemukan dan mungkin paling mudah diingat, karena cukup intuitif. Ingatlah bahwa semua rumus akan didasarkan pada gambar berikut:

Identitas trigonometri dasar
Identitas pertama dari semuanya dikenal sebagai identitas trigonometri dasar , juga dikenal sebagai hubungan antara sinus dan kosinus. Di bawah ini bukti matematisnya: sin² (α) + cos² (α) = 1.
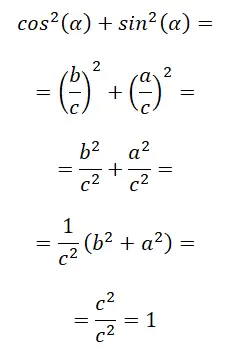
Pada langkah terakhir, pada dasarnya kita menerapkan teorema Pythagoras, karena c² = a² + b², maka tersisa c² / c² yang sama dengan 1. Kesimpulannya, kita dapat menyatakan bahwa: sin² (α) + cos² (α) = 1.
Hubungan antara garis potong dan garis singgung (garis potong kuadrat)
Kedua, kita mempunyai identitas trigonometri yang menghubungkan garis potong dengan garis singgung, ekspresinya adalah sebagai berikut: sec² (α) = 1 + tan² (α) . Pada gambar berikut Anda dapat melihat beberapa rumus pengingat yang membentuk identitas ini dan kemudian prosedur yang harus diikuti untuk sampai pada rumus akhir:
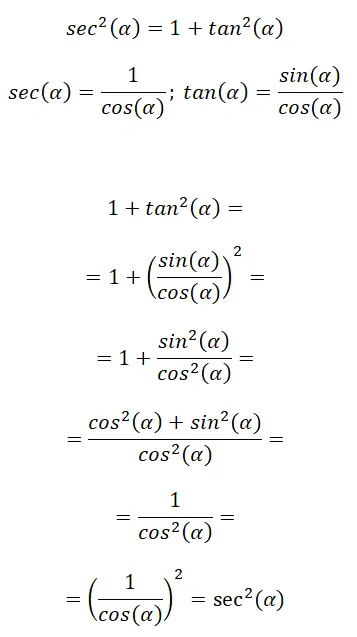
Dalam hal ini, kami menggunakan rumus rasio trigonometri untuk mencari rasio lainnya. Kesimpulannya, kita dapat mengatakan bahwa: detik²(α) = 1 + tan²(α).
Hubungan antara kosekan dan kotangen (kosekan kuadrat)
Dari pengertian kosekan dan kotangen kita dapat menemukan kaitan dalam rumus tangen, berkat inilah kita dapat menyimpulkan identitas trigonometri lainnya: cosec² (α) = 1 + cotg² (α) .
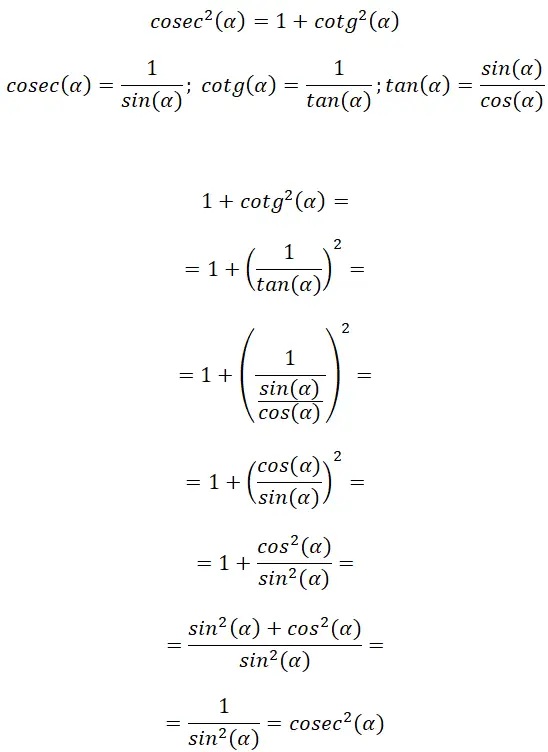
Dengan demonstrasi ini kita dapat memverifikasi bahwa: cosec² (α) = 1 + cotg² (α). Selain itu terlihat bahwa hubungan ini mempunyai kemiripan dengan hubungan sebelumnya, hal ini disebabkan adanya kemiripan antara tangen dan kotangen.
Perbandingan trigonometri sudut penjumlahan dan sudut pengurangan
Rasio penjumlahan sudut atau pengurangan sudut adalah jenis identitas yang diperoleh dengan menghitung rasio trigonometri penjumlahan atau pengurangan dua sudut. Misalnya kita ingin menghitung sinus 90 + 60, ada serangkaian rumus yang memudahkan penghitungan ini. Di bawah ini adalah daftar semua rumus identitas trigonometri gaya ini:
Sinus jumlah sudut: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Pengurangan sinus sudut: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Kosinus jumlah sudut: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Pengurangan cosinus sudut: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Garis singgung jumlah sudut: tan (α + β ) = (tan (α) + tan ( β )) (1 – tan (α) tan ( β ))
Pengurangan tangen sudut: tan(α – β ) = (tan(α) + tan( β )) (1 + tan(α)tan( β ))
Jelas sekali bahwa menghitung sinus 150º lebih mudah daripada menggunakan rumus yang baru saja kami jelaskan untuk menghitung sinus (90º + 60º). Jadi mengapa rumus ini penting? Jawabannya adalah identitas ini memungkinkan kita menghitung perbandingan trigonometri sudut kompleks dari sudut yang lebih sederhana. Oleh karena itu, jika kita menghafal perbandingan sudut-sudut penting (paling relevan), kita tidak perlu menggunakan kalkulator untuk menghitung perbandingan sudut yang lebih kompleks seperti 150º.
Perbandingan trigonometri sudut ganda
Saat kita ingin menghitung perbandingan trigonometri sudut ganda (2α) , kita dapat melakukannya melalui serangkaian identitas. Lebih tepatnya, kita dapat melakukan ini melalui rumus yang sangat mirip dengan yang baru saja kita bahas di bagian sebelumnya. Karena, jika kita mengubah β menjadi α, pada ekspresi sebelumnya, kita mendapatkan (α + α), yang setara dengan (2α). Dengan mengingat hal ini, kita dapat memperoleh identitas berikut:
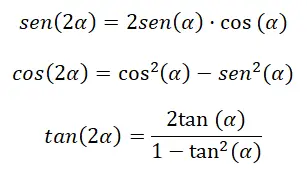
Anda dapat melihat demonya di bawah ini:
Sinus sudut ganda: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Kosinus sudut ganda: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Sudut singgung rangkap dua: tan (2α) = 2 tan (α) (1 – tan² (α))
Perbandingan trigonometri setengah sudut
Selain itu, ada identitas yang memungkinkan kita menghitung rasio trigonometri setengah sudut (α/2) :
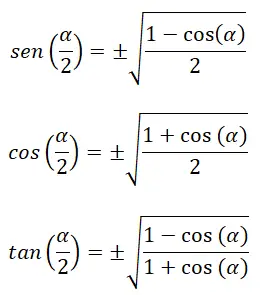
Diantara rumus yang sudah diketahui berikut ini:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – dosa²( β )
Jika kita membuat β = α/2, maka kita dapat membuktikan identitas ini, dengan mengurangkan dua persamaan dalam kasus sinus, menjumlahkannya dalam kasus cosinus, dan membagi dua rumus yang diperoleh (yaitu sinus dan kosinus) dalam kasus garis singgung. Namun tetap mengisolasi rasio yang ingin kita hitung dalam rumus yang kita peroleh di bawah ini:
Sudut setengah sinus: 1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) 2
Cosinus setengah sudut: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) 2
Perbandingan trigonometri sudut rangkap tiga
Dalam kasus memiliki sudut rangkap tiga (3α) , kita juga dapat menggunakan identitas tertentu untuk menghitung rasio trigonometrinya. Identitas tersebut berasal dari rumus berikut yang telah dijelaskan: identitas sudut rangkap, identitas sudut ganda, dan identitas dasar trigonometri.
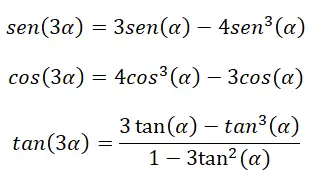
Untuk membuktikan identitas tersebut, kita harus menggunakan rumus jumlah sudut:
Sinus jumlah sudut: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Kosinus jumlah sudut: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Jadi jika kita menerapkan rumus sudut rangkap dalam persamaan yang baru saja kita bicarakan dan menerapkan identitas dasar trigonometri, kita dapat membuktikan identitasnya. Perlu disebutkan bahwa penggunaan identitas trigonometri dasar memungkinkan kita mengubah semua rasio dalam ekspresi menjadi satu. Inilah sebabnya rumus sinus sudut rangkap tiga hanya terdiri dari sinus dan rumus kosinus hanya berisi cosinus. Di bawah ini Anda dapat melihat prosedur lengkapnya:
Sinus tripel sudut: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin³ (α) – sin³ (α) + 2 sin (α) – 2 sin³ (α) =
= 3 dosa (α) – 4 dosa³ (α)
Kosinus sudut tripel: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Terakhir, tangen sudut rangkap tiga dapat dihitung dengan dua cara: yang pertama dengan membagi rumus sinus dengan rumus cosinus dan yang kedua dengan mensubstitusikan persamaan tangen sudut rangkap ke dalam rumus berikut untuk tangen sudut rangkap tiga. jumlah sudut: tan (α + 2α) = (tan (α) + tan (2α)) (1 – tan (α) tan (2α)).
Identitas trigonometri menurut jenis sudut
Penting untuk mengomentari serangkaian rumus yang merupakan aturan yang memungkinkan penghitungan rasio trigonometri secara langsung dan cepat . Faktanya, mereka juga dapat dianggap sebagai identitas trigonometri, karena mereka memenuhi karakteristik yang sama dengan semua ekspresi yang baru saja kita bicarakan. Lebih tepatnya, rumus ini memungkinkan kita menentukan hubungan trigonometri suatu sudut dari hubungannya dengan sudut lain.
sudut yang saling melengkapi
Sudut-sudut yang berkomplemen (α dan β ) adalah sudut-sudut yang jumlahnya sama dengan 90º, sehingga jika dijumlahkan akan diperoleh sudut siku-siku. Untuk menentukan bahwa α adalah sudut komplementer dari β , kita harus menyelesaikan persamaan yang sangat sederhana: α = 90 – β , jika hasil persamaannya sesuai, maka kita dapat menegaskan bahwa kedua sudut tersebut saling melengkapi. Berkat identitas ini kita dapat menyimpulkan perbandingan trigonometri suatu sudut dengan sudut lainnya.
Sinus sudut komplementer: sin (90º – α) = cos (α)
Kosinus sudut komplementer: cos (90º – α) = sin (α)
Garis singgung sudut komplementer: tan (90º – α) = cotan (α)
Kosekan sudut komplementer: cosec (90º – α) = sec (α)
Garis potong sudut komplementer: sec (90º – α) = cosec (α)
Kotangen sudut komplementer: kotan (90º – α) = tan (α)
sudut tambahan
Sudut bersuplemen (α dan β ) adalah sudut yang jumlahnya sama dengan 180º atau π radian, oleh karena itu kita dapat menyimpulkan rumus α + β = 180º. Atau dengan kata lain, jika sudut bersuplemen α adalah β , maka persamaan berikut β = 180 – α harus dipenuhi. Kemudian Anda bisa melihat daftar identitas yang dapat kami simpulkan dari sudut berikut:
Sinus sudut bersuplemen: sin (180º – α) = sin (α)
Kosinus sudut tambahan: cos (180º – α) = -cos (α)
Garis singgung sudut bersuplemen: tan (180º – α) = -tan (α)
Kosekan sudut tambahan: cosec (180º – α) = cosec (α)
Garis potong sudut bersuplemen: detik (180º – α) = -detik (α)
Kotangen sudut bersuplemen: kotan (180º – α) = -kotan (α)
sudut konjugasi
Sudut konjugasi (α dan β ) adalah sudut yang jumlahnya sama dengan 360º atau 2π radian, oleh karena itu kita dapat menyimpulkan rumus α + β = 360º. Dan dari rumus pertama ini, kita dapat menyatakan salah satu sudut ke sudut yang lain sebagai berikut: α = 360º – β atau β = 360º – α. Sekarang kami akan menunjukkan kepada Anda persamaan sudut konjugasi:
Sinus sudut konjugasi: sin (360º – α) = – sin (α)
Kosinus sudut konjugasi: cos (360º – α) = cos (α)
Garis singgung sudut konjugasi: tan (360º – α) = – tan (α)
Kosekan sudut konjugasi: cosec (360º – α) = – cosec (α)
Garis potong sudut konjugasi: sec (360º – α) = sec (α)
Kotangen sudut konjugasi: kotan (360º – α) = – kotan (α)
sudut yang berlawanan
Sudut berhadapan atau sudut negatif (α dan β ) adalah yang mempunyai nilai bilangan yang sama, namun mempunyai tanda yang berbeda, contoh sudut jenis ini adalah 30º dan -30º. Perlu diingat bahwa tanda negatif menunjukkan putaran searah jarum jam, sedangkan sudut positif menunjukkan putaran berlawanan arah jarum jam.
Sinus sudut berhadapan: sin (-α) = – sin (α)
Cosinus sudut berhadapan: cos (-α) = cos (α)
Garis singgung sudut berhadapan: tan (-α) = – tan (α)
Kosekan sudut berhadapan: cosec (-α) = – cosec (α)
Garis potong dari sudut yang berlawanan: sec (-α) = sec (α)
Kotangen sudut berhadapan: kotan (-α) = – kotangen (α)
Sudut yang berbeda 90º atau sudut plus/minus π/2
Sudut yang berbeda 90º atau sudut plus/minus π/2 (α dan β ) adalah sudut yang mempunyai selisih 90º. Oleh karena itu, dapat dinyatakan sebagai β – α = 90º, dimana β lebih besar 90º dari α . Sudut-sudut ini juga memiliki serangkaian rumus yang menghubungkan perbandingan trigonometri kedua sudut.
Sinus sudut yang berbeda 90º: sin (90º + α) = cos (α)
Kosinus sudut yang berbeda 90º: cos (90º + α) = -sin (α)
Garis singgung sudut yang berbeda 90º: tan (90º + α) = – cotan (α)
Kosekan sudut yang berbeda 90º: cosec (90º + α) = sec (α)
Garis potong sudut yang berbeda 90º: sec (90º + α) = -cosec (α)
Kotangen sudut yang berbeda 90º: kotan (90º + α) = -cotan (α)
Sudut yang berbeda 180º atau sudut plus/minus π
Sudut plus/minus π (α dan β ) setara dengan sudut yang berbeda 180º. Oleh karena itu, dapat dinyatakan dengan rumus berikut: β – α = 180º, dimana β 180º lebih besar dari α . Selanjutnya, kami tunjukkan identitas trigonometri yang menghubungkan perbandingan trigonometri sudut-sudut berikut:
Sinus sudut yang berbeda 180º: sin (180º + α ) = -sin ( α )
Kosinus sudut yang berbeda 180º: cos (180º + α ) = -cos ( α )
Garis singgung sudut yang berbeda 180º: tan (180º + α ) = tan ( α )
Kosekan sudut yang berbeda 180º: cosec (180º + α ) = -cosec ( α )
Garis potong sudut yang berbeda 180º: sec (180º + α ) = -sec ( α )
Kotangen sudut yang berbeda 180º: kotan (180º + α ) = kotan ( α )
Transformasi perbandingan trigonometri
Terakhir, ada identitas trigonometri yang memungkinkan kita menyatakan rasio trigonometri tertentu melalui operasi lain . Jadi jika kita mempunyai jumlah rasio dan ingin menyatakannya sebagai suatu produk, kita dapat menggunakan rumus berikut. Meskipun sayangnya tidak ada ekspresi untuk setiap operasi aritmatika, Anda hanya dapat beralih dari penjumlahan atau pengurangan ke perkalian dan sebaliknya .
Ubah penjumlahan atau pengurangan menjadi hasil perkalian
Empat rumus berikut membantu kita menghitung penjumlahan dan pengurangan fungsi trigonometri:
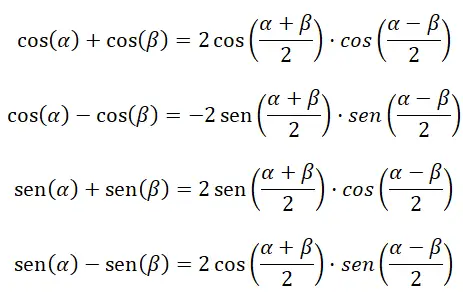
Ubah hasil kali menjadi penjumlahan atau pengurangan
Empat rumus berikut membantu kita menghitung produk fungsi trigonometri: