Identitas terkenal (atau produk terkenal)

Di sini Anda akan menemukan penjelasan tentang resolusi semua jenis identitas terkenal (atau produk terkenal). Anda akan dapat melihat rumus dari semua identitas penting, serta contoh dan latihan yang diselesaikan langkah demi langkah. Selain itu, kami akan menunjukkan kepada Anda untuk apa aturan matematika terkenal ini digunakan.

👉👉 Di bawah ini kami menjelaskan setiap identitas penting langkah demi langkah, tetapi jika mau, Anda dapat langsung menuju ke tabel 😉 di mana semua rumus dirangkum . 👈👈

Apa yang dimaksud dengan identitas terkenal (atau produk terkenal)?

Identitas luar biasa , juga disebut produk luar biasa atau persamaan luar biasa , adalah aturan matematika yang memungkinkan penyelesaian operasi dengan polinomial secara langsung.

Rumus identitas yang paling umum dan umum adalah kuadrat suatu jumlah , kuadrat selisih (atau pengurangan), dan jumlah dikali selisihnya .

identitas atau persamaan produk yang menonjol

Namun di bawah ini kami tidak hanya akan mengajari Anda cara menghitung produk terkenal tersebut, tetapi kami juga akan menunjukkan kepada Anda semua jenis identitas penting yang ada.

Rumus identitas (atau produk) yang terkenal

Setelah kita melihat definisi produk yang terkenal (atau kesetaraan yang penting), kita akan melihat apa rumus untuk identitas yang terkenal. Di sisi lain, jika Anda tertarik dengan demo rumus, Anda dapat melihat rumusnya dengan mengklik tombol “lihat demo”.

kuadrat dari suatu jumlah

Kuadrat suatu jumlah , atau jumlah kuadrat , adalah salah satu identitas utama yang menonjol. Lebih tepatnya, ini adalah binomial dengan dua suku positif pangkat 2, artinya ekspresi aljabarnya adalah (a+b) 2 .

Jadi, rumus kuadrat suatu jumlah adalah:

identitas terkenal dikuadratkan dengan jumlah

Jika kita memulai dari binomial positif yang dipangkatkan menjadi 2:

(a+b)^2

Secara matematis, kuadrat di atas setara dengan faktornya

(a+b)

dikalikan dengan dirinya sendiri:

(a+b)^2=(a+b)\cdot (a+b)

Jadi, kita mengalikan polinomial menggunakan sifat distributif:

\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}

Dari empat istilah yang diperoleh,

ab

Dan

ba

terlihat serupa sehingga kita dapat mengelompokkannya:

a^2+ab+ba+b^2 = a^2+2ab+b^2

Sedemikian rupa sehingga kita telah sampai pada ekspresi rumus jumlah kuadrat, yang merupakan turunannya:

(a+b)^2= a^2+2ab+b^2

Sebagai rasa ingin tahu, pengembangan ekspresi untuk jenis produk luar biasa ini disebut trinomial kuadrat sempurna.

Sehingga kuadrat suatu jumlah sama dengan kuadrat suku pertama, ditambah dua kali hasil kali suku pertama dan suku kedua, ditambah kuadrat suku kedua.

Jadi untuk menyelesaikan penjumlahan kuadrat, tidak cukup dengan menaikkan setiap penjumlahan ke keduanya, tetapi, selain itu, kedua penjumlahan tersebut harus dikalikan satu sama lain dan dengan 2. Penting untuk mengingat hal ini karena kesalahan yang sangat umum dari jenis ini produk Sungguh luar biasa melupakan istilah ini.

identitas polinomial dan binomial yang terkenal

Contoh:

  • Hitung identitas penting berikut dengan menerapkan rumus yang sesuai:

(x+5)^2

Seperti yang baru saja kita lihat, rumus persamaan penting dari jumlah kuadrat adalah:

(a+b)^2=a^2+2ab+b^2

Oleh karena itu, kita harus mengidentifikasi parameternya terlebih dahulu

a

Dan

b

dari rumus tersebut. Pada kasus ini,

a

mewakili

x

dari pasangan dan

b

sesuai dengan nomor 5:

\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}

Nah, sekarang kita sudah mengetahui nilai-nilainya

a

dan dari

b,

kita dapat menggunakan rumus binomial positif kuadrat untuk mencari hasilnya:

contoh identitas kuadrat yang terkenal

kuadrat perbedaan

Kuadrat perbedaan , atau kuadrat selisih , adalah salah satu dari 3 identitas penting yang paling banyak digunakan. Secara khusus, ini sesuai dengan binomial yang dibentuk oleh suku positif dan suku negatif lainnya yang dipangkatkan menjadi 2, artinya ekspresi aljabarnya adalah (ab) 2 .

Jadi, rumus kuadrat selisih (atau kuadrat pengurangan) adalah sebagai berikut:

produk luar biasa kuadrat

Dari ekspresi binomial pengurangan kuadrat:

(a-b)^2

Jelasnya, pangkat sebelumnya sama dengan hasil kali faktornya

(a-b)

dikalikan dengan dirinya sendiri:

(a-b)^2= (a-b)\cdot (a-b)

Sekarang kita mengalikan kedua tanda kurung dengan menerapkan sifat distributif:

\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}

Jadi, Anda hanya perlu mengelompokkan istilah-istilah serupa untuk menyelesaikan pemeriksaan rumus:

a^2-ab-ba+b^2 = a^2-2ab +b^2

Maka rumus kuadrat selisih dibuktikan secara matematis:

(a-b)^2=a^2-2ab+b^2

Sehingga kuadrat selisihnya sama dengan kuadrat suku pertama, dikurangi dua kali hasil kali suku pertama dan suku kedua, ditambah kuadrat suku kedua.

Mengenai persamaan jumlah kuadrat yang luar biasa, kita tidak boleh lupa untuk memasukkan suku tengah rumusnya, karena persamaan berikut ini salah:

kesalahan identitas penting yang umum

Contoh:

  • Selesaikan persamaan penting berikut dari perbedaan kuadrat:

(x-3)^2

Ini adalah hasil kali penting dari pengurangan kuadrat, oleh karena itu perlu menerapkan rumus yang sesuai:

(a-b)^2=a^2-2ab+b^2

Selanjutnya, kita harus mengidentifikasi nilai-nilai yang tidak diketahui.

a

Dan

b

dari rumus tersebut. Pada kasus ini,

a

adalah variabelnya

x

Dan

b

sesuai dengan nomor 3:

\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}

Perhatikan bahwa tanda negatif bukan merupakan bagian dari parameter

b,

tetapi Anda harus selalu mengambil angka tanpa tanda untuk menerapkan rumus ini dengan benar.

Oleh karena itu kita sudah mengetahui nilai-nilai

a

dan dari

b

, oleh karena itu cukup dengan mengganti nilai-nilai ini ke dalam rumus untuk menyelesaikan identitas penting:

contoh dan latihan diselesaikan selangkah demi selangkah dengan persamaan yang penting

jumlah berdasarkan perbedaan

Hasil kali penjumlahan dan selisih adalah salah satu dari 3 identitas penting yang paling banyak digunakan. Seperti namanya, ini adalah binomial positif dikalikan dengan binomial terkonjugasinya (binomial yang sama tetapi dengan tanda tengahnya diubah), artinya ekspresi aljabar dari jenis hasil kali luar biasa ini adalah (a +b) · (ab) .

Rumus identitas luar biasa hasil kali penjumlahan dan selisih adalah sebagai berikut:

identitas, produk dan persamaan menonjol dari SMA 2, 3 dan 4 yang

Mulai dari hasil perkalian suatu penjumlahan dengan pengurangan dua suku apa pun:

(a+b)\cdot (a-b)

Untuk mendemonstrasikan rumusnya, kita hanya perlu mengalikan tanda kurung pertama dengan tanda kurung kedua menggunakan sifat distributif:

\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}

Sekarang kami mengelompokkan istilah serupa menjadi satu:

a^2 -ab+ba-b^2=a^2-b^2

Dan kita telah mencapai ekspresi kesetaraan yang luar biasa. Dengan demikian rumusan untuk jenis identitas yang luar biasa ini ditunjukkan:

(a+b)\cdot (a-b) =a^2-b^2

Jadi, hasil kali jumlah dengan selisih dua besaran sama dengan selisih kuadrat kedua besaran tersebut. Atau dengan kata lain, mengalikan jumlah dua suku berbeda dengan mengurangkan kedua suku yang sama sama dengan mengkuadratkan masing-masing 2 suku dan mengurangkannya.

Contoh:

  • Temukan, dengan menggunakan rumus yang sesuai, hasil kali penting berikut dari penjumlahan dengan selisih dua suku berbeda:

(x+2)\cdot (x-2)

Seperti yang kita lihat di atas, rumus persamaan penting suatu jumlah dikalikan selisihnya adalah sebagai berikut:

(a+b)\cdot (a-b) =a^2-b^2

Pertama-tama, yang perlu kita lakukan adalah mengidentifikasi nilai-nilai huruf tersebut

a

Dan

b

dari rumus tersebut. Pada kasus ini

a

sesuai dengan variabelnya

x

Dan

b

sesuai dengan nomor 2.

\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}

Dan ketika kita sudah mengetahui nilai apa yang diambil parameternya

a

Dan

b,

Kami menerapkan rumus untuk hasil kali jumlah dan selisihnya:

kuadrat dari trinomial

Kuadrat suatu trinomial (polinomial yang terdiri dari 3 suku) sama dengan kuadrat suku pertama, ditambah kuadrat suku kedua, ditambah kuadrat suku ketiga, ditambah dua kali suku pertama kali suku kedua, ditambah dua kali suku pertama dengan yang ketiga, ditambah dua kali yang kedua untuk yang ketiga.

Apa rumus untuk semua identitas, produk, atau kesetaraan yang menonjol?

Dari kuadrat trinomial apa pun:

(a+b+c)^2

Kuadrat di atas dapat dikalikan dengan trinomialnya sendiri:

(a+b+c)^2 = (a+b+c)(a+b+c)

Sekarang kita selesaikan perkalian polinomial:

(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2

Dan terakhir, kami mengelompokkan istilah serupa:

a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc

Dengan cara ini, kita telah sampai pada ekspresi rumusnya, sehingga rumus kuadrat trinomial ditunjukkan:

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

Contoh:

  • Temukan persamaan penting berikut ini:

\left(x^2+x+3\right)^2

Rumus kuadrat trinomial adalah:

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

Seperti dalam semua persamaan penting, Anda harus terlebih dahulu mengidentifikasi nilai-nilai yang tidak diketahui dalam rumusnya. Dalam latihan ini

a

Timur

x^2,

koefisien

b

sesuai dengan

x,

Dan

c

adalah istilah independen 3:

\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}

Dan bila kita sudah mengetahui nilainya, cukup substitusikan nilai tersebut ke dalam rumus dan lakukan perhitungan:

kalkulator identitas, produk, dan persamaan penting

Identitas (atau produk) terkenal dipotong dadu

Kita baru saja mempelajari semua identitas terkenal yang dikuadratkan, yaitu semua jenis identitas penting yang dibentuk oleh pangkat yang dipangkatkan menjadi 2. Nah, sekarang kita akan menganalisis identitas terkenal yang dikuadratkan. Tentu saja, rumus identitas pangkat tiga sedikit lebih rumit, namun juga sangat berguna.

kubus suatu jumlah

Produk kubus yang terkenal dari suatu penjumlahan adalah binomial (polinomial dengan hanya dua monomial) pangkat 3 yang kedua elemennya positif. Oleh karena itu, secara aljabar, pangkat tiga suatu jumlah dinyatakan sebagai (a+b) 3 .

Rumus persamaan pangkat tiga suatu jumlah adalah:

Apa saja produk, identitas, atau ikatan yang terkenal?

Dimulai dari pangkat tiga binomial positif:

(a+b)^3

Pangkat di atas dapat difaktorkan ke dalam perkalian faktor tersebut

(a+b)

menurut kuadratnya:

(a+b)^3=(a+b)\cdot (a+b)^2

Demikian pula, seperti yang kita lihat dalam persamaan kuadrat, binomial

(a+b)

Hal ini dapat diselesaikan dengan rumus kuadrat suatu jumlah:

(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)

Lalu kita mengalikan kedua polinomial tersebut:

\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}

Terakhir, kita hanya perlu mengelompokkan istilah-istilah serupa:

a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3

Dan dengan demikian rumus identitas penting dari jumlah pangkat tiga binomial diverifikasi:

(a+b)^3 = a^3+3a^2b+3ab^2 +b^3

Singkatnya, jumlah yang dipangkatkan menjadi 3 sama dengan pangkat tiga dari bilangan pertama, ditambah tiga kali kuadrat bilangan pertama kali bilangan kedua, ditambah tiga kali bilangan pertama kali kuadrat bilangan kedua, ditambah pangkat tiga dari bilangan kedua.

Contoh:

  • Selesaikan identitas penting berikut dari jumlah pangkat tiga menggunakan rumus yang sesuai:

(x+2)^3

Dalam soal ini kita mempunyai binomial pangkat 3 yang kedua sukunya positif. Oleh karena itu kita harus menggunakan rumus jumlah pangkat tiga:

(a+b)^3 = a^3+3a^2b+3ab^2 +b^3

Sekarang kita perlu mencari nilai parameternya

a

Dan

b

dari rumus tersebut. Pada kasus ini,

a

sesuai dengan variabelnya

x

Dan

b

adalah nomor 2.

\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}

Yang dengannya kami menghitung produk penting dengan mengganti nilai

a

dan dari

b

dalam rumus:

10 contoh produk atau identitas terkenal

kubus perbedaan

Kubus selisih , atau pangkat tiga pengurangan , adalah binomial pangkat 3 yang mempunyai suku bertanda negatif. Jadi, ekspresi matematis untuk jenis produk luar biasa ini adalah (ab) 3 .

Rumus pangkat tiga selisih (atau pengurangan) adalah:

identitas kubik yang luar biasa, produk atau persamaan

Jelas sekali, pembuktian rumus ini sangat mirip dengan pembuktian hasil penjumlahan pangkat tiga. Namun dalam kasus ini, kita mulai dari binomial pangkat tiga negatif:

(a-b)^3

Jelasnya, potensiasi sebelumnya dapat diuraikan menjadi produk faktornya

(a-b)

dikalikan dengan kuadratnya:

(a-b)^3=(a-b)\cdot (a-b)^2

Jadi, saat kita mempelajari identitas kuadrat yang terkenal, binomial

(a-b)

Dapat dihitung dengan rumus kuadrat selisih:

(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)

Kami sekarang menghasilkan produk dari dua polinomial:

\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}

Dan langkah terakhir adalah mengelompokkan istilah-istilah serupa:

a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3

Dengan demikian, rumus identitas penting dari binomial yang dikurangkan dan dipangkatkan ke pangkat tiga telah diverifikasi:

(a-b)^3 = a^3-3a^2b+3ab^2-b^3

Jadi selisih (atau pengurangan) yang dipangkatkan menjadi tiga sama dengan pangkat tiga dari bilangan pertama, dikurangi tiga kali kuadrat bilangan pertama kali bilangan kedua, ditambah tiga kali bilangan pertama kali kuadrat bilangan kedua, dikurangi pangkat tiga bilangan kedua.

Contoh:

  • Hitung binomial pangkat tiga berikutnya (selisih) menggunakan rumus yang sesuai:

(3x-2)^3

Dalam latihan ini, kita mempunyai pasangan dengan elemen positif dan elemen negatif. Oleh karena itu kita harus menggunakan rumus selisih pangkat tiga:

(a-b)^3 = a^3-3a^2b+3ab^2 -b^3

Pertama, seperti biasa, kami mengidentifikasi nilai dari hal-hal yang tidak diketahui

a

Dan

b

dari rumus tersebut. Pada kasus ini

a

mewakili monomial

3x

Dan

b

adalah suku independen dari binomial, yaitu 2.

\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}

Perhatikan bahwa parameternya

b

sama dengan 2, tanpa tanda negatif dari angka tersebut. Penting untuk mengingat hal ini untuk menerapkan formula dengan benar.

Terakhir, kita menemukan jati diri yang luar biasa dengan mengedepankan nilai-nilai

a

dan dari

b

dalam rumus:

mengembangkan identitas, produk, dan kesetaraan yang luar biasa

Tabel ringkasan identitas terkenal

Singkatnya, kami telah membuat tabel dengan semua identitas (atau produk) terkenal yang pernah kami lihat, sehingga akan lebih mudah bagi Anda untuk mempelajarinya. 😉

formula identitas atau persamaan produk unggulan

Latihan terpecahkan dari identitas (atau produk) terkenal

Agar Anda dapat memahami gagasan tentang identitas yang luar biasa, yang juga disebut produk luar biasa atau persamaan luar biasa, kami telah menyiapkan beberapa latihan yang diselesaikan langkah demi langkah. Anda dapat mencoba melakukannya dan kemudian memeriksa apakah Anda melakukannya dengan baik dengan solusi latihannya.

⬇⬇ Jangan lupa bahwa Anda dapat menanyakan semua pertanyaan Anda kepada kami di bawah di komentar! ⬇⬇

Latihan 1

Perluas identitas penting berikut (jumlah kuadrat):

\text{A)} \ (x+3)^2

\text{B)} \ (6x+2)^2

\text{C)} \ \left(x^2+7\right)^2

\text{D)} \ (5x+8y)^2

Semua identitas penting dalam soal adalah jumlah kuadrat, jadi dalam hal ini kita harus selalu menerapkan rumus yang sama:

(a+b)^2=a^2+2ab+b^2

\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}

\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}

\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}

\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}

Latihan 2

Kembangkan produk penting berikut (perbedaan dikuadratkan):

\text{A)} \ (x-2)^2

\text{B)} \ (3-7x)^2

\text{C)} \ \left(x^2-6\right)^2

\text{D)} \ (-3x+y)^2

Semua hasil kali penting dalam latihan ini adalah pengurangan kuadrat, jadi kita hanya perlu menerapkan satu rumus:

(a-b)^2=a^2-2ab+b^2

\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}

\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}

\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}

\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}

Latihan 3

Kembangkan persamaan penting berikut (hasil perkalian jumlah dengan perbedaan):

\text{A)} \ (x+5)(x-5)

\text{B)} \ (2x+6)(2x-6)

\text{C)} \ (x+7)(x-7)

\text{D)} \ (x-4y)(x+4y)

Karena semua persamaan penting dalam latihan ini adalah perkalian jumlah dengan selisih, maka persamaan tersebut diselesaikan dengan rumus yang sama:

(a+b)\cdot (a-b) =a^2-b^2

\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}

\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}

\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}

\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}

Latihan 4

Selesaikan semua identitas penting berikut:

\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)

\text{B)} \ \left(4x^2+2y^3\right)^2

\text{C)} \ \left(6x^3-4y^4\right)^2

\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)

\text{E)} \ \left(5x^2-9x\right)^2

\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}

\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}

\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}

\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}

\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}

Latihan 5

Hitung produk penting berikut:

\text{A)} \ (x+4)^3

\text{B)} \ \left(x^2-5\right)^3

\text{C)} \ \left(2x-1\right)^3

\text{D)} \ (5x+2)^3

Untuk menemukan semua hasil kali penting dari soal tersebut, perlu menerapkan rumus jumlah dan selisih pangkat tiga sesuai dengan kasus:

(a+b)^3 = a^3+3a^2b+3ab^2 +b^3

(a-b)^3 = a^3-3a^2b+3ab^2-b^3

\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}

\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}

\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}

\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}

Latihan 6

Selesaikan persamaan penting berikut ini:

\text{A)} \ \left(x^2+x+5\right)^2

\text{B)} \ \left(x^2+3x-4\right)^2

\text{C)} \ \left(4x^2-6x+3\right)^2

\text{D)} \ \left(x^3-3x^2-9x\right)^2

Untuk menyelesaikan semua identitas penting ini, kita perlu menggunakan rumus kuadrat trinomial, yaitu:

(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}

\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}

\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}

\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}

Latihan 7

Hitung identitas penting berikut dengan akar dan pecahan (kesulitan tinggi):

\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2

\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)

\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2

\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)

Bagian A) terdiri dari pengurangan kuadrat, jadi untuk menyelesaikannya harus diterapkan rumus yang sesuai dan, sebagai tambahan, harus diingat bahwa jika suatu akar dikuadratkan, maka disederhanakan:

\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}

Bagian B) membahas penjumlahan dengan pengurangan dan monomial memiliki koefisien pecahan, yang dengannya hasil kali penting ini harus ditentukan menggunakan rumus penjumlahan dengan pengurangan dan sifat-sifat pecahan:

\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}

Persamaan penting di bagian C) adalah jumlah yang dipangkatkan menjadi 2 dan, juga, terdiri dari pecahan. Oleh karena itu, untuk menghitungnya kita perlu menggunakan rumus jumlah kuadrat ditambah sifat-sifat pecahan:

\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}

Identitas penting terakhir berkaitan dengan jumlah dikalikan selisih dengan koefisien irasional, jadi kita menerapkan rumus untuk jumlah dikali selisih lalu menyederhanakan akar kuadratnya:

\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}

Tipe identitas penting lainnya

Semua identitas penting yang kita bahas di atas adalah yang paling umum digunakan. Namun, dalam matematika terdapat jenis produk penting lainnya yang juga menarik untuk diketahui, karena digunakan untuk tujuan yang berbeda.

jumlah kubus

Jumlah kubus sama dengan binomial yang kedua sukunya positif dan, terlebih lagi, akar pangkat tiganya eksak. Oleh karena itu, ekspresi aljabar jumlah kubus adalah a 3 +b 3 .

identitas, produk, atau ikatan penting terselesaikan

Rumus perkalian penting ini digunakan untuk memfaktorkan suatu polinomial, yaitu melalui rumus tersebut kita mengubah polinomial menjadi hasil kali binomial dengan trinomial.

Agar Anda dapat melihat cara melakukannya, berikut ini contoh penerapan identitas luar biasa ini:

x^3+8

Memang benar ekspresi sebelumnya terdiri dari penjumlahan pangkat tiga karena akar pangkat tiga dari monomial

x^3

eksak (tidak memberikan angka desimal) dan angka 8 juga:

\sqrt[3]{x^3} = x

\sqrt[3]{8} = 2

x^3+8=x^3+2^3

Oleh karena itu, kita dapat menggunakan rumus jumlah kubus sempurna untuk mengubah ekspresi kubik menjadi hasil kali binomial dengan trinomial:

a^3+b^3 = (a+b)(a^2-ab+b^2)

\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}

perbedaan kubus

Selisih (atau pengurangan) kubus adalah binomial yang terdiri dari suku positif dan suku negatif yang akar pangkat tiganya eksak. Dengan kata lain, selisih kubus dinyatakan dalam bentuk a 3 -b 3 .

Latihan yang diselesaikan untuk memfaktorkan polinomial dengan identitas penting

Mari kita buat sebuah contoh sehingga Anda dapat melihat bagaimana tipe identitas yang luar biasa ini diselesaikan:

x^3-27

Perbedaan pangkat tiga karena keduanya merupakan akar pangkat tiga dari monomial

x^3

karena 27 benar:

\sqrt[3]{x^3} = x

\sqrt[3]{27} = 3

x^3-27=x^3-3^3

Oleh karena itu, Anda dapat menggunakan rumus selisih kubus sempurna untuk memfaktorkan binomial:

a^3-b^3 = (a-b)(a^2+ab+b^2)

\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}

Hasil kali binomial dengan suku yang sama

Hasil kali penting ini digunakan untuk mengubah hasil kali dua binomial yang memiliki suku yang sama menjadi polinomial kuadrat.

identitas, produk, atau persamaan yang luar biasa pdf

Berikut adalah contoh rumit dari jenis produk luar biasa ini:

\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}

lebih banyak identitas

Meskipun identitas terkenal adalah yang paling terkenal karena paling umum, perlu dicatat bahwa ada lebih banyak identitas dengan nama lain juga. Berikut daftar identitas lain yang kurang dikenal jika Anda penasaran:

  • Identitas Lagrange:

    • (a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2

    • (a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2

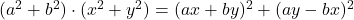
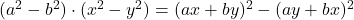
  • Identitas legenda:

    • (a+b)^2+(a-b)^2=2(a^2+b^2)

    • (a+b)^2-(a-b)^2=4ab

    • (a+b)^4-(a-b)^4=8ab(a^2+b^2)

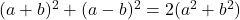
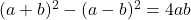
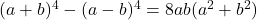
  • Identitas Argand:

    • (x^2+x+1)(x^2-x+1) = x^4+x^2+1

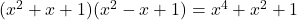
  • Identitas Gaussian:

    • a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)

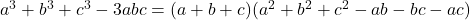
    • a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]

Aplikasi identitas terkenal

Jika Anda sudah sampai sejauh ini, berarti Anda sudah tahu cara melakukan perhitungan dengan identitas penting. Terang! Tapi sungguh… untuk apa identitas terkenal itu? Dan kapan identitas penting digunakan?

Seperti yang telah kita lihat di seluruh artikel ini, tujuan utama dari identitas penting adalah untuk menyederhanakan perhitungan. Artinya, berkat produk yang luar biasa, kita dapat secara langsung menyelesaikan pangkat tertentu dari polinomial kompleks tanpa harus melakukan operasi yang sulit.

Namun persamaan penting juga memiliki fungsi lain, seperti memfaktorkan polinomial dan menyelesaikan kuadrat. Kemudian kita akan melihat terdiri dari apa saja masing-masing aplikasi ini.

Memfaktorkan polinomial

Beberapa jenis polinomial yang sangat spesifik dapat difaktorkan dengan identitas penting. Misalnya, jika kita menemukan polinomial yang terdiri dari dua suku yang merupakan kuadrat sempurna (akar kuadratnya eksak), kita dapat memfaktorkannya menggunakan rumus persamaan luar biasa dari hasil kali penjumlahan dan selisih:

a^2-b^2 =(a+b)(a-b)

x^2-9 =(x+3)(x-3)

Demikian pula, trinomial yang memperhatikan identitas penting dari kuadrat penjumlahan atau pengurangan dapat difaktorkan:

a^2+2ab+b^2=(a+b)^2

x^2+4x+4=(x+2)^2

a^2-2ab+b^2=(a-b)^2

x^2-10x+25=(x-5)^2

Demikian pula, setelah suatu polinomial difaktorkan, akar-akar (atau nol) dari polinomial tersebut dapat ditemukan. Meski begitu, konsep ini sedikit lebih rumit untuk dipahami, jadi jika Anda lebih tertarik, kami sarankan untuk mencari penjelasannya di mesin pencari di website kami (kanan atas), karena kami memiliki artikel lengkap yang menjelaskannya.

penyelesaian persegi

Menyelesaikan kuadrat adalah prosedur matematika yang digunakan untuk mengubah trinomial kuadrat menjadi jumlah kuadrat plus (atau minus) suatu angka.

Diberikan trinomial apa pun:

ax^2+bx+c

Kemudian trinomial tersebut dapat diubah menjadi ekspresi berikut:

a(x+h)^2+k

dimana parameternya

h

Dan

k

dihitung dengan rumus berikut:

h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2

Meskipun bagi Anda tampaknya tidak demikian, kedua rumus ini disimpulkan dari identitas penting. Jadi, berkat produknya yang luar biasa, kotak-kotak itu bisa diselesaikan.

Sebagai contoh, kami akan menerapkan prosedur ini pada trinomial berikut:

2x^2+4x+3

Kami menghitung parameternya

h

Dan

k:

h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1

k=c-ah^2 = 3-2\cdot 1^2 = 1

Dan, oleh karena itu, polinomialnya tetap:

2(x+1)^2+1

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top