Pada artikel ini kami menjelaskan apa itu fungsi yang dibatasi (atas dan bawah). Selain itu, kami juga menunjukkan kepada Anda apa artinya suatu fungsi dibatasi pada suatu titik dan, terakhir, Anda akan menemukan properti dari jenis fungsi ini.
Apa yang dimaksud dengan fungsi terbatas?
Fungsi berbatas adalah fungsi yang grafiknya berada dalam batas. Artinya, suatu fungsi dibatasi di atas jika terdapat bilangan K sehingga tidak ada nilai fungsi yang lebih besar dari K (f(x)≤K), dan suatu fungsi dibatasi di bawah jika terdapat bilangan K sedemikian sehingga lebih kecil dari semua nilai fungsi (f(x)≥K). Oleh karena itu, fungsi terbatas adalah fungsi yang dibatasi di atas dan di bawah.
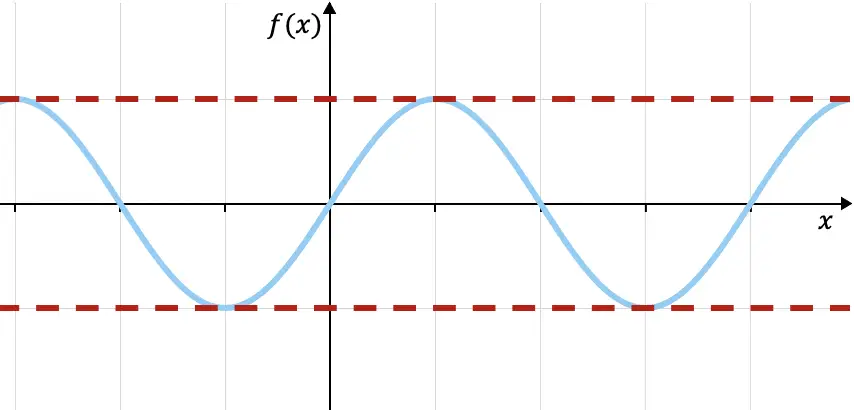
Misalnya, fungsi sinus trigonometri pada grafik di atas dibatasi di bagian atas oleh f(x)=1 dan dibatasi di bawah oleh f(x)=-1 (garis putus-putus merah), karena semua nilai dari fungsi berada dalam dua batas ini. Anda dapat melihat lebih banyak properti dari fungsi ini di tautan berikut:
➤ Lihat: Karakteristik fungsi sinus
dibatasi fungsi di atas
Namun tidak semua fungsi dibatasi atas dan bawah, suatu fungsi hanya dapat dibatasi atas atau bawah.
Fungsi berbatas di atas adalah fungsi yang tidak melebihi nilai tertentu, dengan syarat terpenuhi:
![]()
dimana nilai K adalah batas atas fungsi.
Misalnya, parabola berikut dibatasi di bagian atas oleh K=7, namun fungsinya tidak dibatasi di bagian bawah karena cabang-cabangnya memanjang hingga tak terhingga.

Logikanya, jika suatu fungsi dibatasi oleh K=7, maka fungsi tersebut juga dibatasi oleh K=8 dan nilai yang lebih tinggi.
Batas atas terkecil disebut batas atas dan diwakili oleh sup(f) . Selanjutnya, jika fungsi tersebut mencapai batas atas domainnya, kita dapat mengatakan bahwa titik tersebut adalah maksimum absolut dari fungsi tersebut.
➤ Lihat: apa yang dimaksud dengan maksimum dan minimum suatu fungsi?
Dalam kasus kita, fungsi tersebut dibatasi secara geometris oleh K=7, sehingga merupakan titik ekstrem atas dan maksimum absolut dari fungsi tersebut.
fungsi dibatasi di bawah ini
Fungsi-fungsi yang dibatasi di bawah ini adalah fungsi-fungsi yang tidak mempunyai nilai kurang dari suatu bilangan tertentu, yaitu memenuhi persamaan matematika berikut:
![]()
Dimana nilai K merupakan batas bawah fungsi tersebut.
Di bawah ini Anda memiliki representasi grafis dari fungsi eksponensial yang dibatasi oleh K=3:

Jelasnya, fungsi tersebut juga dibatasi oleh nilai yang kurang dari K=3.
Seperti sebelumnya, batas bawah terbesar disebut batas bawah dan diwakili oleh inf(f) . Selanjutnya, jika fungsi tersebut mencapai titik ekstrem bawah tersebut dalam domainnya, kita dapat mengatakan bahwa titik ini adalah minimum absolut dari fungsi tersebut.
Dalam hal ini, K=3 bukanlah nilai minimum mutlak dari fungsi tersebut, karena fungsi tersebut mencapai nilai ini pada tak terhingga dan, oleh karena itu, berada di luar domainnya. Dengan kata lain, f(x)=3 adalah asimtot horizontal dari fungsi tersebut .
Ada teorema yang memungkinkan Anda mengetahui apakah suatu fungsi dibatasi di bagian atas dan bawah tanpa representasi grafisnya. Klik di sini untuk melihat apa teorema Weierstrass.
➤ Lihat: Teorema Weierstrass
Fungsi dibatasi pada satu titik
Kita baru saja mempelajari pengertian membatasi suatu fungsi secara umum, namun kita juga dapat menganalisis apakah suatu fungsi dibatasi atau tidak pada lingkungan yang lebih kecil, yaitu pada sebagian fungsi.
Ya
![]()
adalah titik dalam domain fungsi dan
![]()
nilai apa pun, kita akan mengatakan bahwa fungsi tersebut dibatasi di atas/di bawah titik tersebut
![]()
jika ada lingkungan
![]()
di mana fungsinya dibatasi di atas/bawah.
Oleh karena itu, suatu fungsi dibatasi pada suatu titik
![]()
jika dibatasi pada bagian atas dan bawah dalam suatu lingkungan
![]()
Jelasnya, jika suatu fungsi dibatasi secara umum, maka fungsi tersebut juga dibatasi pada setiap titiknya. Namun yang terjadi adalah kebalikannya, yaitu suatu fungsi dapat dibatasi pada setiap titiknya dan tidak dibatasi pada seluruh domainnya.
Misalnya, fungsi affine berikut dibatasi sebagian di setiap titiknya, namun bukan fungsi berbatas.

Sifat-sifat fungsi yang dibatasi
Fungsi yang dibatasi memiliki sifat-sifat berikut:
- Ya

Dan

adalah dua fungsi yang dibatasi, penjumlahan (atau pengurangan) kedua fungsi tersebut
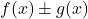
juga merupakan fungsi terbatas.
- Ya

Dan

adalah dua fungsi yang dibatasi, hasil kali kedua fungsi tersebut
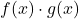
juga merupakan fungsi terbatas.
- Jika suatu fungsi memiliki asimtot vertikal, maka fungsi tersebut tidak dapat dibatasi seluruhnya. Di sisi lain, fungsinya dapat dibatasi ke atas atau ke bawah.
- Setiap fungsi kontinu dan terbatas pada suatu interval dapat diintegralkan.