Fungsi rasional: apa itu, domain, asimtot, grafik, latihan,...

Di sini Anda akan menemukan apa itu fungsi rasional. Selain itu, kami menjelaskan cara menghitung domain dan asimtot fungsi rasional. Dan tidak hanya itu, Anda akan melihat apa saja ciri-ciri fungsi rasional. Terakhir, Anda dapat berlatih dengan latihan langkah demi langkah tentang fungsi rasional.

Apa yang dimaksud dengan fungsi rasional?

Pengertian fungsi rasional adalah sebagai berikut:

Fungsi rasional adalah fungsi yang dibentuk oleh hasil bagi dua polinomial , yaitu fungsi rasional adalah pecahan yang pembilang dan penyebutnya mempunyai polinomial.

Fungsi rasional dicirikan oleh singularitas pada titik di mana penyebutnya hilang.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Fungsi rasional disebut juga fungsi pecahan.

Di sisi lain, fungsi rasional tidak sama dengan fungsi irasional. Fungsi irasional (atau radikal) adalah fungsi yang terdiri dari akar-akar.

Contoh Fungsi Rasional

Untuk lebih memahami pengertian fungsi rasional, kita akan melihat beberapa contoh fungsi jenis ini.

Fungsi rasional dengan polinomial derajat pertama pada pembilang dan penyebutnya:

$f(x)=\cfrac{x+3}{2x-5}$

Jenis fungsi rasional ini disebut juga fungsi homograf .

Fungsi rasional dengan konstanta di pembilangnya dan polinomial di penyebutnya:

$f(x)=\cfrac{7}{x+1}$

Jenis fungsi rasional ini disebut fungsi proporsional terbalik dan digunakan untuk mendefinisikan besaran proporsional terbalik secara matematis.

Fungsi rasional dengan polinomial derajat ketiga pada pembilangnya dan polinomial derajat kedua pada penyebutnya:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Domain fungsi rasional

Suatu bilangan dibagi 0 merupakan suatu ketidakpastian yang menghasilkan tak terhingga (∞), sehingga fungsi rasional akan selalu ada kecuali penyebutnya 0.

Oleh karena itu, domain fungsi rasional terdiri dari semua bilangan real kecuali nilai yang menghilangkan penyebutnya.

Jadi, untuk mendapatkan domain dari suatu fungsi rasional, kita perlu mencari kapan penyebutnya 0, karena titik ini adalah satu-satunya titik yang tidak termasuk dalam domain tersebut.

Mari kita lihat bagaimana domain fungsi rasional dihitung dengan menyelesaikan sebuah contoh:

$f(x)=\cfrac{5x}{x+2}$

Pertama-tama kita atur penyebutnya menjadi 0, lalu kita selesaikan persamaan yang dihasilkan:

$x+2=0$

$x=-2$

Oleh karena itu, jika x adalah -2, penyebutnya adalah 0 dan fungsinya tidak akan ada. Oleh karena itu, domain fungsi tersebut terdiri dari semua bilangan real kecuali x=-2. Hal ini dinyatakan sebagai berikut:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Asimtot fungsi rasional

Salah satu sifat utama fungsi rasional adalah asimtotnya, karena fungsi tersebut menentukan representasi grafisnya.

➤ Lihat: representasi grafis dari suatu fungsi

Asimtot suatu fungsi rasional adalah garis-garis yang didekati grafik fungsi tersebut hingga tak terhingga tetapi tidak pernah menyentuhnya.

Ada tiga jenis asimtot: asimtot vertikal, asimtot horizontal, dan asimtot miring.

Di bawah ini Anda memiliki tiga jenis asimtot yang dapat digambarkan dalam grafik fungsi rasional dengan warna merah.

Asimtot vertikal dari fungsi rasional

Asimtot horizontal dari fungsi rasional

Asimtot miring dari fungsi rasional

Seperti yang Anda lihat, menentukan asimtot suatu fungsi dari grafiknya cukup sederhana, tetapi menghitung asimtot suatu fungsi rasional tanpa representasi grafiknya cukup rumit. Inilah sebabnya kami menyarankan Anda melihat bagaimana asimtot suatu fungsi dihitung di situs web kami.

Ciri-ciri fungsi rasional

Fungsi rasional mempunyai ciri-ciri sebagai berikut:

$f(x)=\cfrac{P(x)}{Q(x)}$

Seperti yang kita lihat di atas, domain fungsi rasional mencakup semua bilangan real kecuali nilai yang menghilangkan penyebut pecahan.

Secara umum, rentang (atau rentang) suatu fungsi rasional mencakup semua bilangan real kecuali nilai yang fungsi tersebut memiliki asimtot horizontal.

Fungsi rasional bersifat kontinu di seluruh domainnya. Atau dengan kata lain, fungsi rasional menunjukkan diskontinuitas pada titik-titik yang tidak termasuk dalam domainnya.

Representasi grafis dari sebagian besar fungsi rasional terdiri dari dua hiperbola.

Beberapa aturan asimtot fungsi rasional dapat disimpulkan dari pembilang polinomial.
$P(x)$

dan polinomial penyebutnya

$Q(x):$
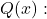
- Suatu fungsi rasional mempunyai asimtot vertikal pada titik-titik yang merupakan akar-akarnya
  $Q(x)$
  
  tapi ini bukan akar dari
  
  $P(x).$
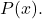
- Jika derajat
  $P(x)$
  
  kurang dari derajat
  
  $Q(x)$
  
  , garis y=0 adalah asimtot horizontal dari fungsi rasional.
- Jika derajat
  $P(x)$
  
  lebih besar dari derajatnya
  
  $Q(x)$
  
  , fungsi rasional tidak memiliki asimtot horizontal.
- Jika derajat
  $P(x)$
  
  adalah satuan yang lebih besar dari derajat
  
  $Q(x)$
  
  dan kedua polinomial tersebut tidak mempunyai akar yang sama, fungsi rasional mempunyai asimtot miring.

Latihan soal fungsi rasional

Latihan 1

Temukan domain dari fungsi rasional berikut:

$f(x)=\displaystyle\frac{4x}{2x+4}$

Lihat solusinya

Ini adalah fungsi rasional, jadi domainnya terdiri dari semua bilangan kecuali bilangan yang menghilangkan penyebutnya, karena fungsi tersebut akan menghasilkan ∞.

Jadi kita menetapkan penyebut bilangan bulat sama dengan nol untuk melihat bilangan mana yang tidak termasuk dalam domain:

$2x+4=0$

Dan kami menyelesaikan persamaan yang dihasilkan:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

Oleh karena itu, domain fungsi hanya terdiri dari bilangan kecuali -2:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Latihan 2

Tentukan titik potong fungsi rasional berikut dengan sumbu kartesius:

$f(x)=\cfrac{x^2-9}{x}$

Lihat solusinya

Titik potong dengan sumbu X

Untuk mencari titik potong fungsi tersebut dengan sumbu X perlu dicari penyelesaiannya

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

Kita memperoleh dua penyelesaian persamaan kuadrat, sehingga fungsi rasional memotong sumbu absis di dua titik berbeda, yaitu:

$\bm{(3,0)\qquad (-3,0)}$

Titik potong dengan sumbu Y

Untuk mencari titik potong dengan sumbu Y harus dilakukan perhitungan

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Bilangan apa pun yang dibagi nol merupakan suatu ketidakpastian yang menghasilkan bilangan tak terhingga. Oleh karena itu, fungsi rasional tidak melewati titik mana pun di atas sumbu Y, yaitu tidak mempunyai titik potong dengan sumbu y.

Latihan 3

Gambarkan fungsi rasional berikut pada grafik:

$y=\cfrac{2x+3}{2x+6}$

Lihat solusinya

Hal pertama yang harus dilakukan adalah menghitung domain dari fungsi tersebut:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Setelah kita mengetahui domain fungsinya, kita membuat tabel nilai:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

Untuk menyelesaikannya, cukup nyatakan titik-titik yang diperoleh pada grafik dan gambarkan hiperbolanya, sehingga menggambar fungsi rasionalnya:

Latihan 4

Tentukan asimtot fungsi rasional yang digambarkan di bawah ini:

Lihat solusinya

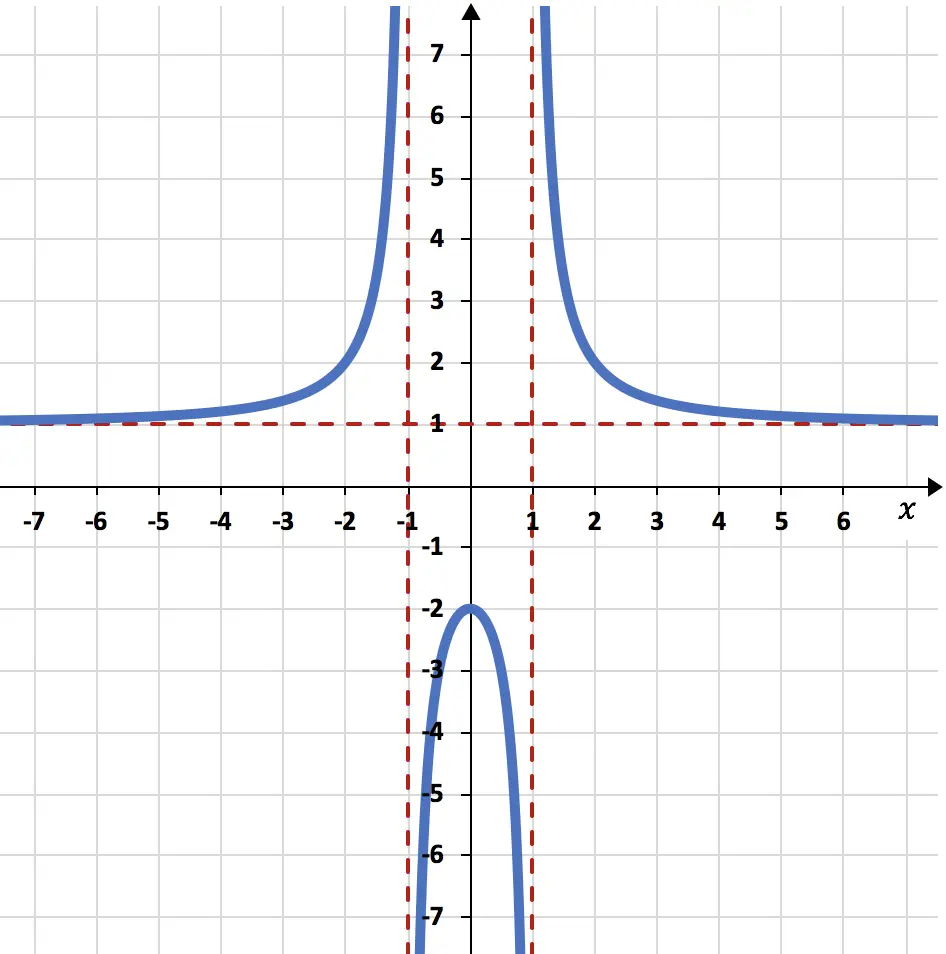
Asimtotnya terlihat sangat jelas pada grafik, karena direpresentasikan sebagai garis putus-putus berwarna merah.

Dalam soal ini, fungsinya sangat dekat dengan garis horizontal y=1 tetapi tidak pernah menyentuhnya. Oleh karena itu, fungsi rasional memiliki satu asimtot horizontal, yaitu y=1.

Demikian pula, representasi grafis dari fungsi tersebut sangat dekat dengan garis vertikal x=-1 dan x=1, tetapi tidak pernah mencapai nilai tersebut. Oleh karena itu, fungsi rasional memiliki dua asimtot vertikal yang berbeda, yaitu x=-1 dan x=1.

Latihan 5

Hitung semua asimtot fungsi rasional berikut:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Catatan: Untuk menyelesaikan latihan ini, kami menyarankan Anda terlebih dahulu membuka tautan di atas tentang cara menghitung asimtot suatu fungsi dan melihat penjelasannya.

Lihat solusinya

asimtot vertikal

Untuk menghitung asimtot vertikal suatu fungsi, pertama-tama kita harus mencari domain fungsi tersebut. Oleh karena itu, kita menetapkan penyebut fungsi rasional sama dengan 0 untuk mencari titik-titik yang tidak termasuk dalam domain:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

Oleh karena itu, domain fungsi tersebut terdiri dari semua bilangan kecuali -1:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Jadi x=-1 bisa menjadi asimtot vertikal. Untuk memeriksanya, kita harus menghitung limit fungsi di titik tersebut:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Oleh karena itu, x=-1 adalah asimtot vertikal dari fungsi rasional, karena limit fungsi pada titik ini memberikan tak terhingga.

asimtot horizontal

Untuk menentukan asimtot horizontal, kita perlu menghitung limit tak terhingga dari fungsi tersebut:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

Dalam hal ini, hasil batas tak terhingga antara tak terhingga adalah pembagian koefisien x pangkat tertinggi, karena pembilang dan penyebutnya berorde sama.

Dua limit tak hingga dari fungsi tersebut memberi kita nilai 3, jadi y=3 adalah asimtot horizontal dari fungsi rasional.

asimtot miring

Karena terdapat asimtot horizontal, maka fungsi rasional tidak mempunyai asimtot miring.

Apa yang dimaksud dengan fungsi rasional?

Contoh Fungsi Rasional

Domain fungsi rasional

Asimtot fungsi rasional

Ciri-ciri fungsi rasional

Latihan soal fungsi rasional

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan