Halaman ini menjelaskan apa itu fungsi proporsionalitas terbalik dan cara membuat grafiknya. Selain itu, Anda akan menemukan semua karakteristik fungsi jenis ini, cara menghitung domainnya, dan juga beberapa contoh serta latihan yang diselesaikan langkah demi langkah untuk latihan.
Apa yang dimaksud dengan fungsi proporsionalitas terbalik?
Fungsi proporsionalitas terbalik adalah fungsi yang menghubungkan dua besaran yang berbanding terbalik, yaitu besaran yang satu bertambah sedangkan besaran yang lain berkurang dan sebaliknya. Secara umum, fungsi proporsionalitas terbalik didefinisikan dengan rumus berikut:
![]()
Emas
![]()
adalah konstanta yang disebut rasio proporsionalitas.
Jadi, fungsi proporsionalitas terbalik selalu terdiri dari pecahan yang penyebutnya polinomial derajat pertama. Oleh karena itu, mereka adalah jenis fungsi rasional.
Contoh fungsi proporsionalitas terbalik:
![]()
Umumnya
![]()
umumnya merupakan variabel bebas dan
![]()
variabel terikat, atau dengan kata lain variabel
![]()
bergantung pada
![]()
Sebaliknya, perbandingan proporsionalitas (suku pembilangnya) bisa positif atau negatif dan tandanya menandai kenaikan atau penurunan fungsi:
- Jika konstan

negatif, fungsinya meningkat.
- Sebaliknya jika konstan

positif maka fungsinya menurun.
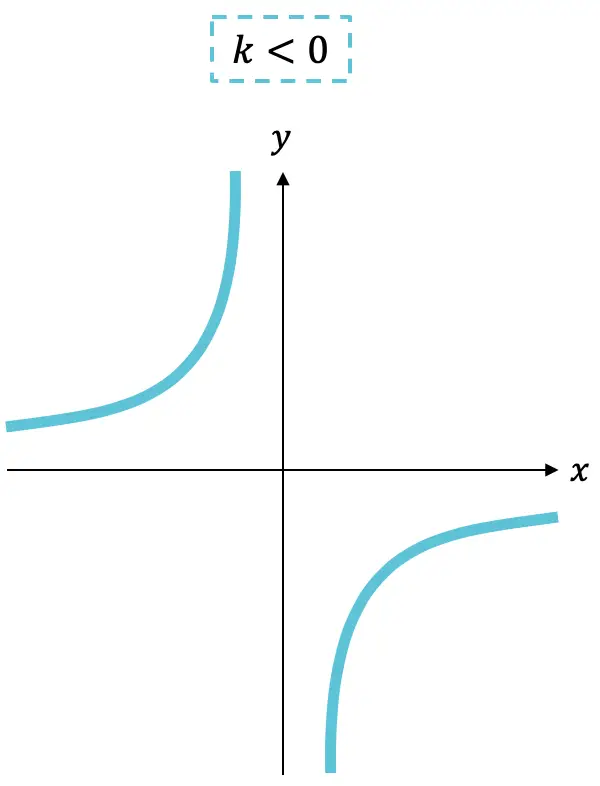
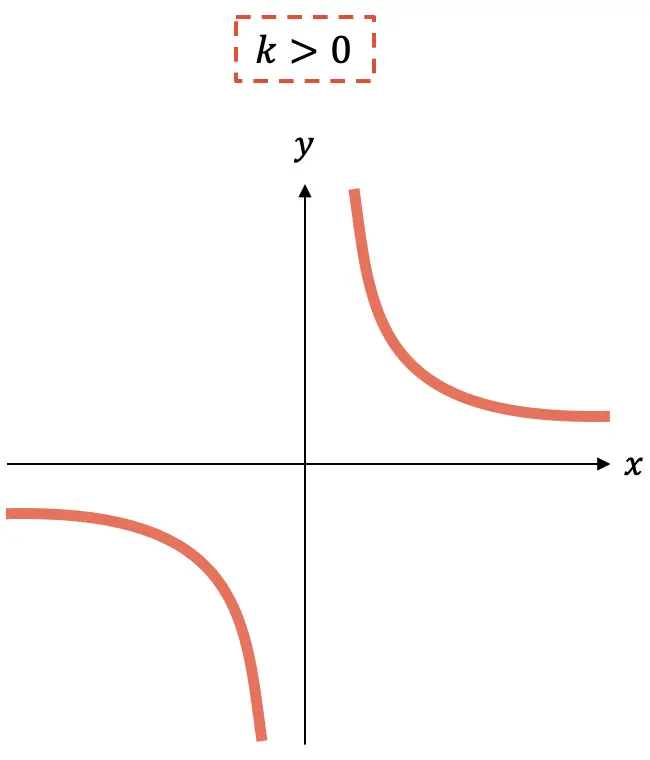
Seperti yang Anda lihat, grafik fungsi proporsionalitas terbalik selalu terdiri dari dua hiperbola yang bergantung pada tanda k , akan berada di satu kuadran atau kuadran lainnya.
Domain fungsi proporsionalitas terbalik
Sebagai salah satu jenis fungsi rasional, domain dari fungsi proporsionalitas terbalik adalah semua bilangan real kecuali bilangan yang hilang dari penyebutnya . Karena penyebutnya tidak akan pernah nol karena akan menghasilkan bilangan tak terhingga.
Sebagai contoh, kita akan menentukan domain dari fungsi proporsionalitas terbalik berikut:
![]()
Untuk mengetahui kapan penyebutnya nol, kita harus menyamakan ekspresinya dengan 0 dan menyelesaikan persamaannya:
![]()
![]()
Jadi, ketika x bernilai 1, penyebutnya akan menjadi nol dan kita memperoleh ketidakpastian. Jadi domain dari fungsi tersebut adalah semua bilangan real dikurangi
![]()
![]()
Cara Membuat Grafik Fungsi Proporsionalitas Terbalik
Kita akan melihat cara membuat grafik fungsi proporsionalitas terbalik menggunakan sebuah contoh.
- Kami akan mewakili fungsi berikut dalam grafik:
![]()
Hal pertama yang perlu kita lakukan adalah mencari domain dari fungsi tersebut. Sebagai pecahan, penyebutnya tidak boleh 0 karena akan menghasilkan bilangan tak terhingga. Oleh karena itu, domainnya akan semuanya x kecuali penyebutnya dibatalkan.
Oleh karena itu, kami menetapkan penyebutnya sama dengan 0 untuk melihat x mana yang tidak termasuk dalam domain:
![]()
![]()
Oleh karena itu, domain dari fungsi tersebut adalah semua bilangan kecuali 2:
![]()
Setelah kami mengetahui nomor mana yang bukan milik domain, kami membuat tabel nilai. Untuk merepresentasikan fungsi proporsionalitas terbalik, perlu menghitung 3 atau 4 titik di kiri dan 3 atau 4 titik di kanan bilangan yang tidak termasuk dalam domain (2):
![]()

Sekarang mari kita nyatakan titik-titik pada grafik :
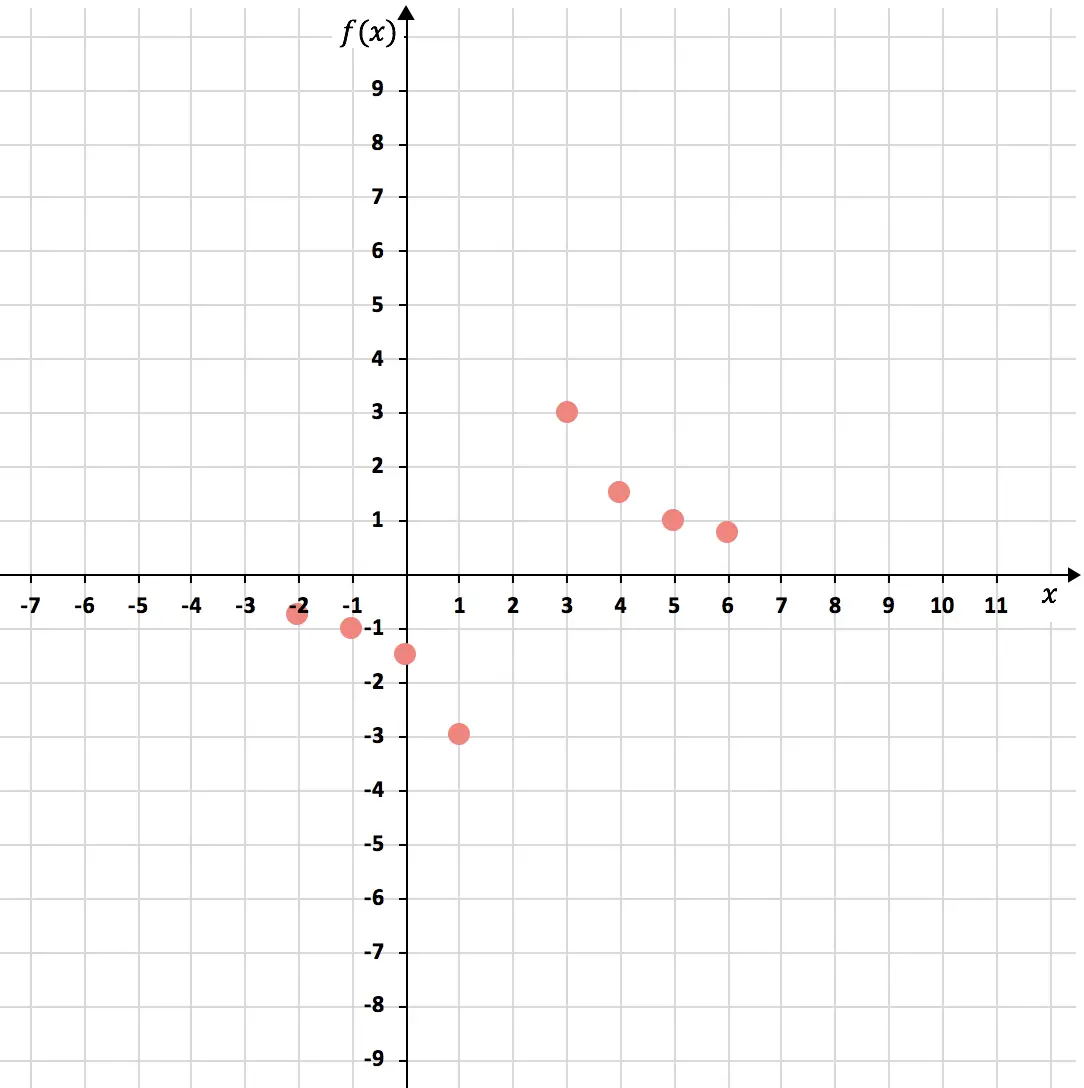
Dan akhirnya kita gabungkan titik-titiknya, membentuk dua hiperbola dari fungsi proporsionalitas terbalik. Selain itu, kami memanjangkan cabang-cabang hiperbola untuk menunjukkan bahwa mereka terus tumbuh:

Perhatikan bahwa fungsinya mendekati
![]()
, baik di kanan maupun di kiri. Akan tetapi, ia tidak pernah mencapai angka 2, ia sangat dekat namun tidak pernah mengenainya. JADI,
![]()
itu adalah asimtot vertikal . Ini karena
![]()
tidak termasuk dalam domain fungsi tersebut dan oleh karena itu, fungsi tersebut tidak ada pada titik tersebut.
Dan hal yang sama terjadi pada sumbu X horizontal. Fungsinya mendekati
![]()
tapi jangan pernah menyentuhnya. Belum,
![]()
adalah asimtot horizontal .
Artinya semua fungsi proporsionalitas terbalik adalah diskontinu karena selalu mempunyai asimtot.
Anda dapat mempelajari lebih lanjut tentang asimtot dan batasan fungsi di situs web kami.
Memecahkan masalah fungsi proporsionalitas terbalik
Latihan 1
Hitung domain dari fungsi proporsionalitas terbalik berikut:
![]()
Fungsi proporsionalitas terbalik tidak akan ada jika penyebutnya 0, karena fungsi tersebut akan menghasilkan ∞. Oleh karena itu, kita perlu menetapkan penyebut fungsi tersebut sama dengan 0 untuk melihat bahwa x menghilangkan penyebutnya dan, oleh karena itu, tidak termasuk dalam domain.
![]()
![]()
![]()
![]()
Latihan 2
Gambarkan fungsi proporsionalitas terbalik berikut:
![]()
Hal pertama yang harus dilakukan adalah menghitung domain dari fungsi tersebut:
![]()
![]()
Setelah kita mengetahui nomor mana yang bukan milik domain, kita membuat array nilai dengan fungsi:

Terakhir, kita nyatakan titik-titik yang diperoleh pada grafik dan menggambar hiperbola, sehingga membentuk fungsi proporsionalitas terbalik:
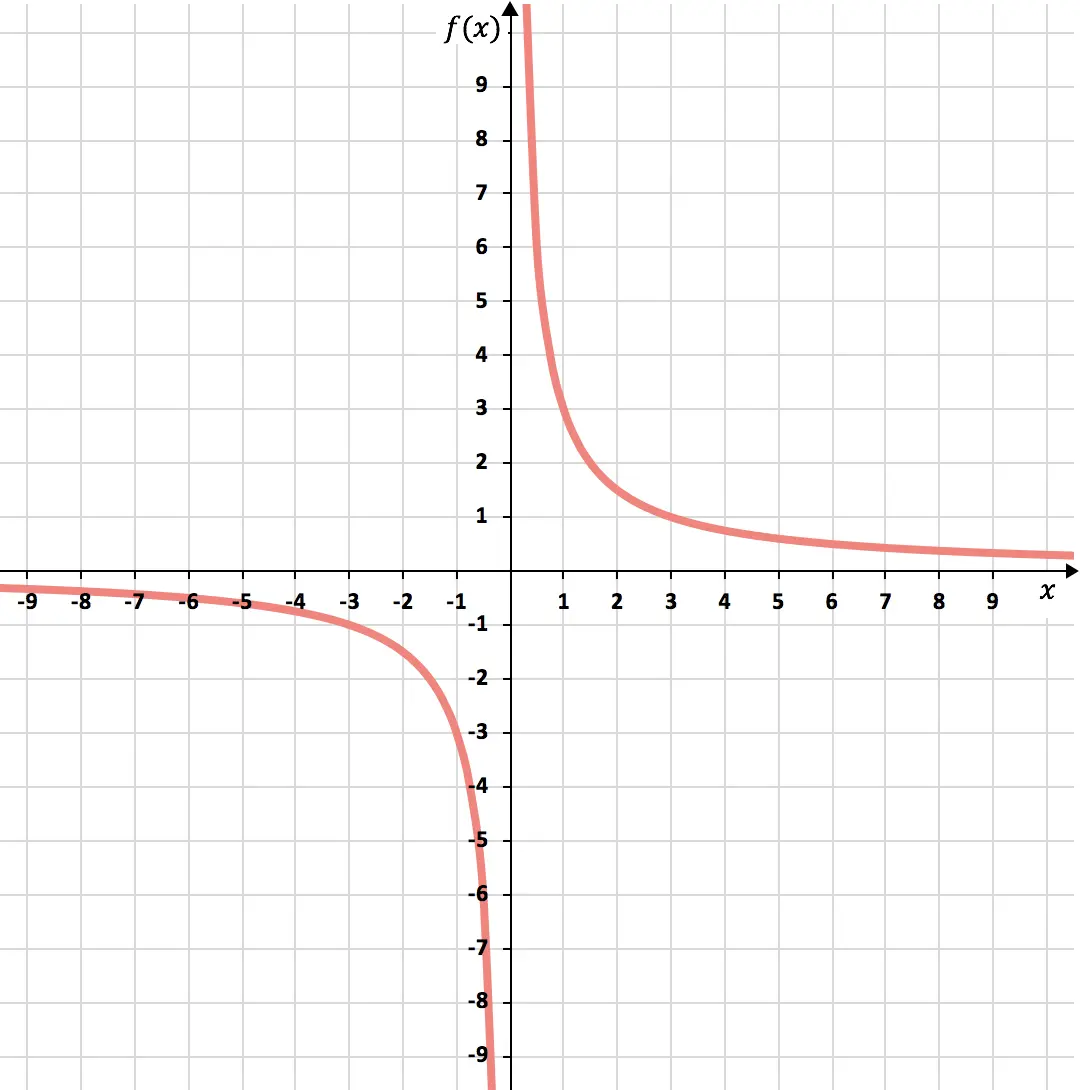
Latihan 3
Gambarkan fungsi proporsionalitas terbalik berikut:
![]()
Hal pertama yang harus dilakukan adalah menghitung domain dari fungsi tersebut:
![]()
![]()
![]()
Setelah kita mengetahui domain fungsinya, kita membuat tabel nilai:

Terakhir, kami merepresentasikan titik-titik yang diperoleh pada grafik dan memplot hiperbola, sehingga membentuk fungsi proporsionalitas terbalik:
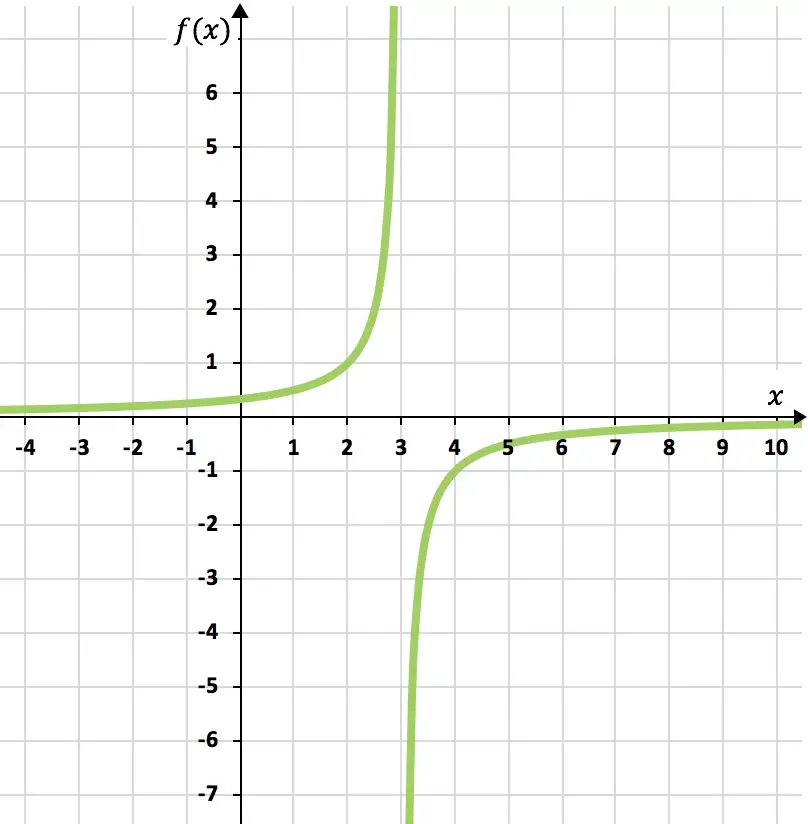
Latihan 4
Gambarkan fungsi proporsionalitas terbalik berikut:
![]()
Pertama, kita perlu menghitung domain dari fungsi tersebut:
![]()
![]()
![]()
![]()
Setelah kita mengetahui domain fungsinya, kita membuat array nilai:
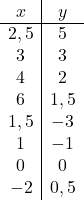
Dan terakhir, kita nyatakan titik-titik yang diperoleh pada grafik dan gambarkan hiperbolanya, sehingga membentuk fungsi proporsionalitas terbalik:
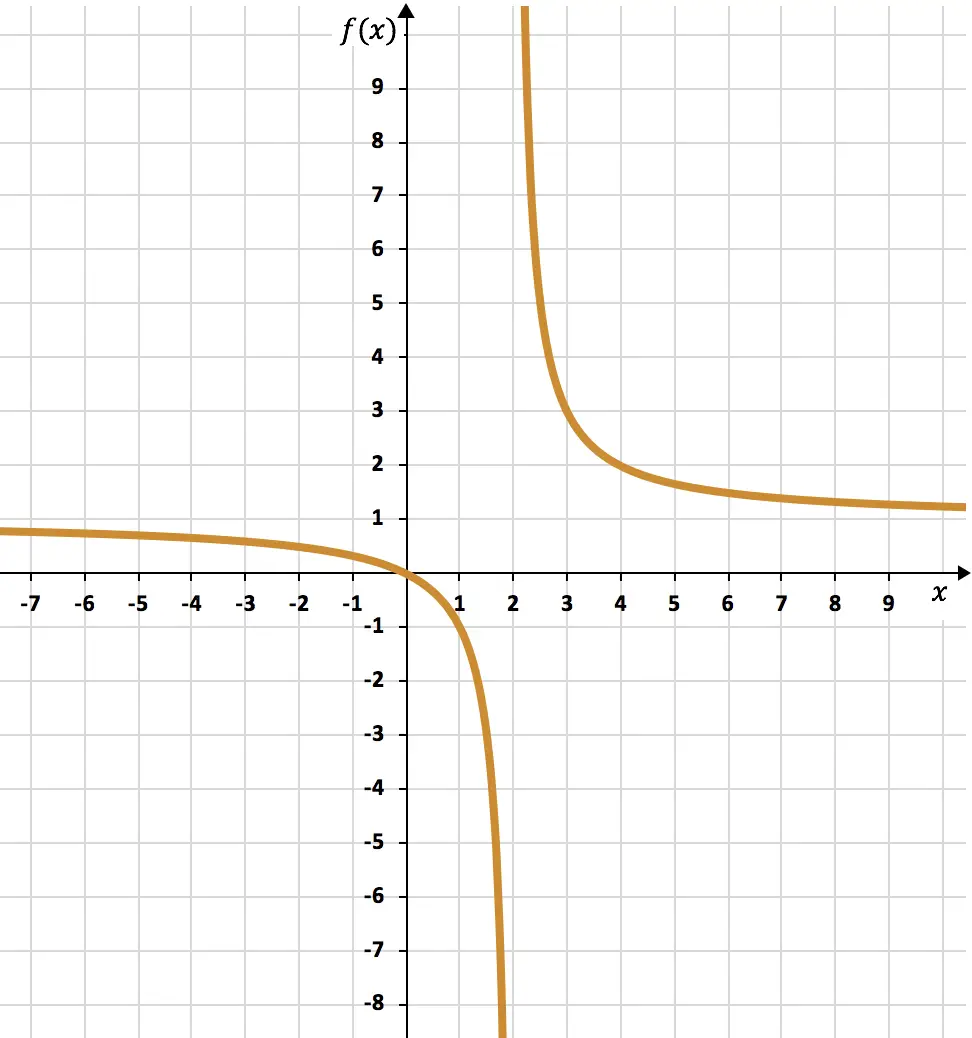
Latihan 5
Gambarkan fungsi rasional berikut:
![]()
Hal pertama yang harus dilakukan adalah menghitung domain dari fungsi tersebut:
![]()
![]()
![]()
![]()
Setelah kita mengetahui domain fungsinya, kita membuat tabel nilai:

Untuk menyelesaikannya, cukup nyatakan titik-titik yang diperoleh pada grafik dan gambarkan hiperbolanya, sehingga membentuk fungsi pecahan:

Penerapan fungsi proporsionalitas terbalik
Fungsi proporsionalitas terbalik muncul dalam banyak kasus dalam fisika dan matematika.
Misalnya, digunakan untuk menggambarkan hubungan antara tekanan dan volume dalam gas ideal yang suhunya konstan k. Fungsi ini disebut hukum Boyle-Mariotte (P×V=k) dan merupakan contoh fungsi proporsionalitas terbalik. Jelasnya, domain definisi fungsi ini terbatas hanya pada cabang positif, karena tidak ada volume atau tekanan negatif.
Hubungan antara intensitas arus dan hambatan listrik dengan beda potensial konstan juga diatur oleh fungsi proporsionalitas terbalik. Fungsi ini dikenal sebagai hukum Ohm (V=I×R).