Pada artikel ini kami akan menjelaskan apa itu fungsi proporsionalitas langsung, apa rumusnya, cara merepresentasikannya dalam grafik, dan cara menghitung persamaannya dari suatu titik tertentu.
Apa yang dimaksud dengan fungsi proporsionalitas langsung?
Fungsi proporsionalitas langsung adalah fungsi yang menghubungkan dua besaran yang berbanding lurus. Oleh karena itu, untuk menghitung nilai variabel terikat (y), nilai variabel terikat (x) harus dikalikan dengan konstanta proporsionalitas.
Fungsi proporsionalitas langsung disebut juga fungsi linier.
Ingatlah bahwa dua besaran berbanding lurus jika besaran yang satu bertambah nilainya sedangkan besaran yang lain juga bertambah, begitu pula sebaliknya.
Rumus fungsi proporsionalitas langsung
Rumus yang mendefinisikan fungsi proporsionalitas langsung adalah sebagai berikut:
![]()
dimana y adalah variabel bebas, x adalah variabel terikat, dan ym adalah kemiringan atau konstanta proporsionalitas fungsi tersebut.
Seperti yang Anda lihat, dengan rumus ini sangat mudah untuk menghitung nilai besaran y, cukup mengalikan nilai besaran x dengan kemiringan fungsi yang merupakan ciri dari setiap fungsi proporsionalitas langsung.
Misalnya, jika kita mempunyai fungsi proporsionalitas langsung berikut:
![]()
Jika kita ingin menentukan besaran y pada saat x sama dengan 5, kita hanya perlu mengalikan kemiringan fungsi (3) dengan 5:
![]()
Representasi grafis dari fungsi proporsionalitas langsung
Selanjutnya kita akan melihat cara membuat grafik fungsi proporsionalitas langsung. Kami akan melakukan latihan berikut sebagai contoh:
![]()
Untuk menyatakan fungsi proporsionalitas langsung pada grafik, cukup tarik garis yang melalui titik asal (titik (0,0)) dan mempunyai kemiringan fungsi tersebut.
Dalam hal ini, fungsi yang ingin kita wakili mempunyai kemiringan
![]()
Oleh karena itu, garis harus bertambah dua satuan y untuk setiap satuan x.
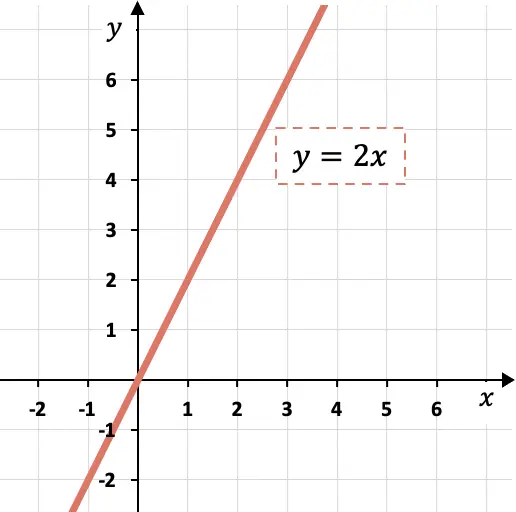
Terlihat dari grafik, jika kemiringannya sama dengan 2, berarti besaran y bertambah dua kali lipat besaran x.
Fungsi proporsionalitas langsung memiliki grafik yang sangat mirip dengan fungsi affine, namun keduanya merupakan jenis fungsi yang berbeda. Apa saja perbedaan fungsi affine dan fungsi linier dapat Anda lihat pada link berikut:
➤ Lihat: perbedaan antara fungsi linier dan affine
Cara mencari fungsi proporsionalitas langsung
Jika kita mengetahui suatu titik pada fungsi proporsionalitas langsung, kita dapat dengan mudah mencari persamaannya. Mari kita lihat bagaimana hal ini dilakukan dengan menyelesaikan masalah fungsi proporsionalitas langsung:
- Banyaknya ruangan yang dicat oleh seorang pelukis kira-kira berbanding lurus dengan jam kerjanya, yaitu semakin banyak jam kerjanya maka semakin banyak pula ruangan yang dapat ia cat. Jika kita mengetahui bahwa dalam waktu 8 jam sehari ia mengecat dua ruangan penuh, apa fungsi proporsionalitas langsung yang menghubungkan jumlah ruangan yang dicat dengan jam kerja?
Pertama, kita perlu menentukan mana yang merupakan variabel terikat dan mana yang bebas. Jumlah potongan yang dicat bergantung pada jam kerja dan bukan sebaliknya. Jadi variabel bebas (x) adalah jumlah jam kerja dan variabel terikat (y) adalah jumlah ruangan yang dicat.
Soal tersebut menunjukkan bahwa seorang pelukis dapat mengecat 2 ruangan dalam waktu 8 jam, sehingga grafik fungsinya harus melalui titik (8,2).
![]()
Selain itu, pernyataan tersebut menunjukkan bahwa kedua besaran mempunyai hubungan berbanding lurus, artinya secara matematis berhubungan dengan rumus fungsi proporsionalitas langsung:
![]()
Sekarang kita dapat menghitung nilai kemiringan fungsi dengan mensubstitusikan koordinat titik (8,2) ke dalam persamaan:
![]()
Dan, akhirnya, kita menyelesaikan persamaan m yang tidak diketahui:
![]()
![]()
![]()
Singkatnya, fungsi proporsionalitas langsung dari soal adalah:
![]()
Anda mungkin juga menyukai: