Pada artikel ini Anda akan menemukan penjelasan yang sangat detail tentang fungsi polinomial yang dilengkapi dengan contoh. Selain itu, Anda akan dapat melihat bagaimana fungsi polinomial digunakan dalam kehidupan sehari-hari berkat latihan yang akan kami sajikan di bagian akhir.
Apa itu fungsi polinomial?
Fungsi polinomial atau fungsi polinomial adalah fungsi yang diberikan oleh ekspresi aljabar yang setara dengan polinomial . Artinya ekspresi tersebut harus mengikuti struktur polinomial: f(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + … + a n x n , bergantung pada struktur yang akan kita gunakan tentukan jenis fungsi polinomial yang akan kita proses. Karakteristik lain yang sangat relevan dari fungsi-fungsi ini adalah bahwa semua eksponen yang tidak diketahui adalah positif dan bilangan bulat .
Bagian dari fungsi polinomial
Kami dapat menyoroti tiga elemen penting mengenai fungsi-fungsi ini:
- Koefisien polinomial: bilangan-bilangan yang menyertai bilangan yang tidak diketahui, misalnya 3 suku berikut adalah koefisien: 3x 2 . Perlu dicatat bahwa jumlah koefisien sama banyaknya dengan jumlah suku dalam polinomial.
- Eksponen atau indeks polinomial: ini adalah pangkat dari yang tidak diketahui, misalnya 2 suku berikut adalah eksponen: 3x 2 . Dan seperti yang telah kami jelaskan, dalam kasus fungsi polinomial, fungsinya akan selalu positif dan bilangan bulat.
- Derajat polinomial: nilai ini setara dengan eksponen derajat tertinggi di antara semua suku yang membentuk polinomial. Dalam kasus polinomial f(x) = 3x 2 – 4x + 2, derajatnya sama dengan dua.
Bagaimana cara mengetahui suatu fungsi polinomial atau tidak?
Untuk mengidentifikasi fungsi polinomial, kita harus melihat apakah fungsi tersebut memenuhi karakteristik yang baru saja kita bicarakan. Kita akan mulai dengan memeriksa apakah ekspresi yang mendefinisikan fungsi tersebut memiliki struktur polinomial : f(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + … + a n x n . Kemudian kita akan memeriksa apakah indeksnya positif dan bilangan bulat, dengan langkah sederhana ini kita akan dapat menentukan apakah suatu fungsi polinomial atau tidak.
Jenis Fungsi Polinomial Beserta Contohnya
Selanjutnya, kami akan menunjukkan kepada Anda berbagai jenis fungsi polinomial yang ada, yang diklasifikasikan menurut derajat polinomialnya. Selain itu, Anda akan menemukan contoh representasi grafis untuk setiap jenis. Berkat contoh fungsi polinomial ini Anda akan dapat melihat perbedaan antara berbagai kategori dengan lebih baik.
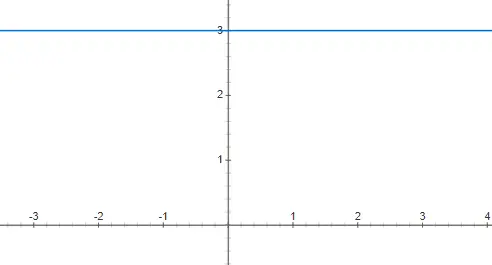
fungsi konstan
Fungsi konstanta ekuivalen dengan polinomial berderajat 0, artinya koefisien x adalah 0. Inilah sebabnya fungsi jenis ini tidak bergantung pada nilai variabel bebas x. Oleh karena itu, representasi grafisnya adalah garis horizontal yang tidak terbatas. Di bawah ini Anda dapat menemukan contoh f(x) = 3 yang diwakili:
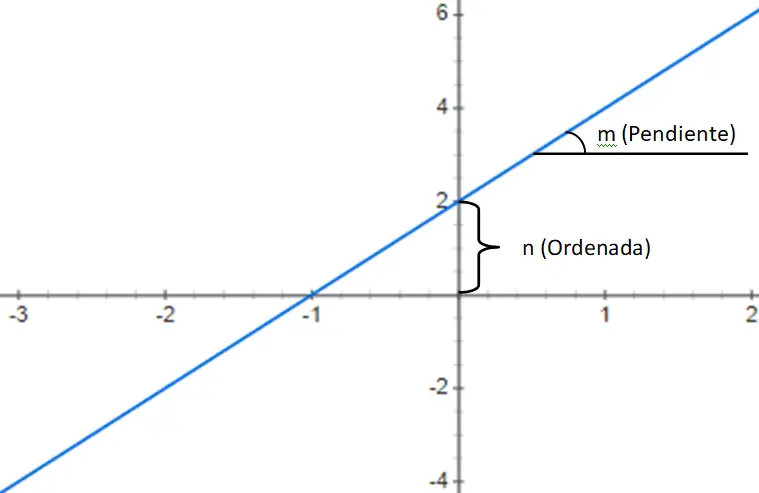
fungsi polinomial derajat pertama
Kedua, kita mencari fungsi polinomial derajat pertama , yang diberikan oleh polinomial derajat 1 dengan struktur sebagai berikut: f(x) = mx + n. Ekspresi ini terdiri dari bilangan yang disebut kemiringan (m) yang mengalikan variabel xy dengan konstanta (n) yang ditambahkan ke hasil kali ini. Jadi, berdasarkan nilai m dan n, kita dapat membedakan tiga jenis fungsi yang berbeda:
- Fungsi affine: subtipe ini dicirikan dengan memiliki nilai n yang berbeda dengan 0, yaitu nilai komputer berbeda dengan 0. Oleh karena itu, fungsi jenis ini tidak melewati titik (0, 0), disebut juga asal. Beri komentar juga jika m < 0 maka fungsinya akan berkurang, sedangkan jika m > 0 maka fungsinya akan meningkat.
- Fungsi linier: Satu-satunya perbedaan fungsi ini dengan fungsi affine adalah n = 0, sehingga tidak memiliki komputer. Oleh karena itu, ekspresi fungsi linier setara dengan f(x) = mx. Tipe ini cukup mudah untuk direpresentasikan karena selalu melewati titik (0, 0) dan dari kemiringannya sudah diperoleh grafiknya.
- Fungsi identitas: tipe terakhir ini adalah subgrup fungsi linier yang an = 0 dan m = 1. Artinya ekspresi tetap f(x) = x, yang representasi grafisnya berupa diagonal yang membentuk sudut 45º dengan salah satu sumbu. Fungsi jenis ini juga melewati titik asal (0, 0).
Di bawah ini, Anda akan menemukan contoh fungsi polinomial derajat pertama, lebih tepatnya fungsi affine f(x) = 3x + 2:
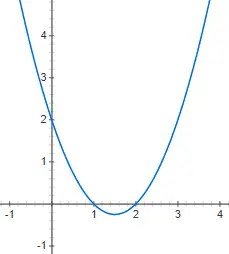
fungsi kuadrat
Fungsi kuadrat atau fungsi kuadrat dinyatakan menggunakan polinomial kuadrat, yang mengikuti struktur: f(x) = ax 2 + bx + c, di mana a berbeda dari 0. Dalam hal ini, representasi grafisnya jauh lebih kompleks, karena merupakan bukan lagi garis lurus, melainkan parabola vertikal . Di bawah ini Anda dapat menemukan representasi fungsi kuadrat f(x) = 2x 2 + 4x – 1:
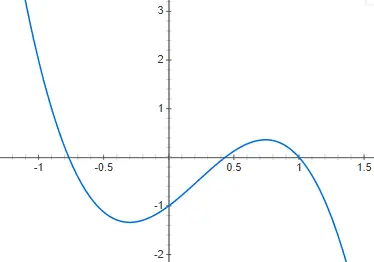
fungsi kubik
Fungsi kubik atau fungsi derajat ketiga diberikan oleh polinomial derajat tiga: f(x) = ax 3 + bx 2 + cx + d, berbeda dari 0. Representasi fungsi gaya ini bahkan lebih kompleks daripada yaitu derajat kedua, karena dapat mempunyai beberapa bentuk yang berbeda. Meskipun bentuk dasarnya, atau paling tidak yang paling umum, adalah bentuk yang akan kami tunjukkan pada contoh berikut, f(x) = 2x 3 – 4x 2 + 2x – 2:
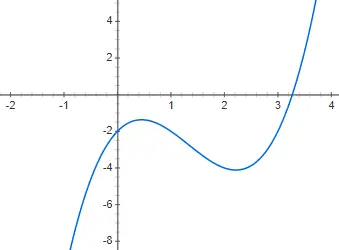
Sifat-sifat fungsi polinomial
Fungsi polinomial memiliki serangkaian sifat atau ciri yang membedakannya dengan fungsi lainnya, dan kami akan merincinya sejelas mungkin di bawah ini. Dengan cara ini, ketika Anda melihat fungsi seperti ini, akan sangat mudah bagi Anda untuk mengidentifikasinya:
- Daerah asal suatu fungsi polinomial sama dengan semua bilangan real : Dom f = R atau Dom f = (-∞, ∞), oleh karena itu keduanya kontinu pada seluruh himpunan bilangan real.
- Titik potongnya pada sumbu Y setara dengan (0, a 0 ), 0 adalah suku bebas.
- Memotong sepanjang sumbu X beberapa kali sama dengan atau kurang dari derajat polinomial.
- Fungsi polinomial tidak memiliki asimtot.
- Jika eksponen semua suku ganjil, maka grafiknya simetris terhadap titik asal koordinat, sedangkan jika eksponen semua suku genap maka grafiknya simetris terhadap sumbu OY.
- Banyaknya titik belok suatu fungsi gaya ini sama dengan atau kurang dari n – 2, dengan n adalah derajat.
- Jumlah maksimum dan minimum relatif suatu fungsi gaya ini sama dengan atau kurang dari n – 1, dengan n adalah derajat.
Bagaimana cara menganalisis fungsi polinomial?
Untuk menganalisis fungsi polinomial, kita harus mengikuti prosedur yang sama seperti yang kita gunakan untuk menganalisis fungsi lainnya. Dalam daftar berikut kami telah merangkum berbagai elemen yang harus dipelajari atau ditangani:
- Domain dan jangkauan
- Titik perpotongan dengan sumbu horizontal dan vertikal
- Monoton (naik dan turun, maksimal dan minima)
- Kelengkungan (dalam fungsi derajat lebih besar dari satu)
Tentu saja, kita dapat membawa analisis ini ke tingkat yang lebih tinggi dan mempelajari banyak elemen lainnya, meskipun hal ini sudah cukup. Karena, dengan mengetahui elemen-elemen ini, Anda akan memiliki gambaran yang jelas tentang seperti apa fungsinya dan Anda akan dapat merepresentasikannya secara grafis.
Latihan fungsi polinomial
Selanjutnya, kami menawarkan serangkaian latihan untuk berlatih merepresentasikan fungsi , khususnya fungsi polinomial. Dengan cara ini Anda akan menggabungkan semua konsep yang dijelaskan dalam artikel ini:
Latihan 1
Gambarkan fungsi polinomial derajat pertama berikut f(x) = x + 2 dan sebutkan jenisnya:
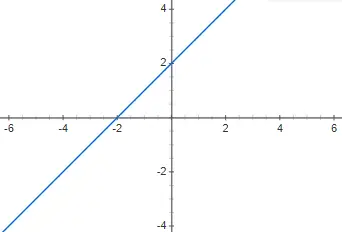
Merupakan fungsi polinomial affine derajat pertama, karena berbeda dari 0 dan m berbeda dari 0.
Latihan 2
Gambarkan fungsi polinomial kuadrat berikut f(x) = x 2 + x – 2:
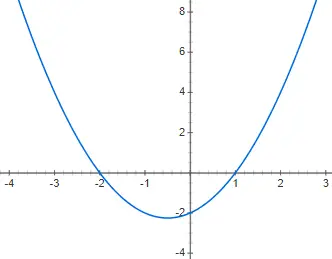
Latihan 3
Gambarkan fungsi polinomial derajat ketiga berikut f(x) = x 2 + x – 2: