▷ Apa itu dan bagaimana merepresentasikan fungsi kuadrat (atau parabola)

Halaman ini menjelaskan apa itu fungsi kuadrat beserta seluruh ciri-cirinya: kelengkungan, titik sudut, titik potong dengan sumbu, dll. Anda juga akan mempelajari cara merepresentasikan fungsi kuadrat pada grafik. Dan terakhir, Anda dapat berlatih dengan contoh, latihan langkah demi langkah, dan soal fungsi kuadrat.

Apa itu fungsi kuadrat?

Pengertian fungsi kuadrat adalah sebagai berikut:

Dalam matematika, fungsi kuadrat (atau parabola) adalah fungsi polinomial berderajat 2, yaitu fungsi yang suku derajat tertingginya berpangkat kedua. Oleh karena itu, rumus fungsi kuadrat adalah:

$f(x)=ax^2+bx+c$

Emas:

$ax^2$

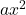
adalah suku kuadrat.
$bx$

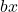
adalah istilah linier.
$c$

adalah istilah independen.

Domain suatu fungsi kuadrat selalu terdiri dari bilangan real.

$\text{Dom } f=\mathbff{R}$

Kecekungan dan konveksitas suatu fungsi kuadrat

Menganalisis kelengkungan fungsi kuadrat atau parabola sangatlah sederhana, karena hanya bergantung pada koefisien kuadrat.

Jika koefisien
$a$

positif, fungsi kuadratnya cembung (dalam bentuk

$\bm{\cup}$

). Oleh karena itu, KTT ini bersifat minimum.
Jika koefisien
$a$

negatif, fungsi kuadratnya cekung (berbentuk seperti

$\bm{\cap}$

). Oleh karena itu, puncaknya adalah maksimum.

Catatan: Komunitas matematika masih belum sepenuhnya setuju dan, oleh karena itu, beberapa profesor mengatakan sebaliknya: mereka menyebut suatu fungsi cekung yang berbentuk a

$\bm{\cup}$

, dan fungsi cembung yang berbentuk

$\bm{\cap}$

. Pokoknya yang penting bentuknya apa fungsinya, apapun namanya.

Titik puncak fungsi kuadrat

Untuk membuat grafik fungsi kuadrat, perlu diketahui koordinat titik puncak parabola.

Untuk mencari titik puncak suatu fungsi kuadrat, kita perlu menghitung koordinat X suatu titik dengan menggunakan rumus berikut:

$\displaystyle x=\frac{-b}{2a}$

Kemudian kita dapat mencari koordinat titik lainnya dengan menghitung bayangan fungsi pada titik tersebut:

$\displaystyle f\left(\frac{-b}{2a}\right)$

Jadi koordinat titik puncak suatu fungsi kuadrat (atau parabola) adalah:

$\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)$

Titik potong dengan sumbu fungsi kuadrat

Parabola selalu memotong sumbu y (sumbu Y), dan hal ini terjadi ketika

$x=0.$

Oleh karena itu, untuk menghitung titik potong suatu fungsi kuadrat dengan sumbu Y harus diselesaikan

$f(0).$

Misalnya titik potong fungsi kuadrat berikut dengan sumbu OY adalah:

$f(x)=x^2-2x+1$

$f(0)=0^2-2\cdot 0+1 = 1$

$\bm{(0,1)}$

Sebaliknya, titik potong suatu fungsi kuadrat dengan sumbu x (sumbu X) terjadi ketika

$f(x)=0.$

Jadi untuk menghitung titik potong dengan sumbu X Anda harus menyelesaikan persamaannya

$f(x)=0.$

Sebagai contoh, di bawah ini adalah perhitungan titik potong dengan sumbu OX fungsi kuadrat yang sama:

$f(x)=x^2-2x+1$

$0=x^2-2x+1$

Kami menyelesaikan persamaan kuadrat dengan rumus umum:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1$

Maka titik potong fungsi kuadrat dengan sumbu X adalah:

$\bm{(1,0)}$

Dalam kasus ini, kita hanya mendapatkan satu solusi persamaan kuadrat, namun kita bisa mendapatkan dua solusi. Dalam hal ini berarti fungsi kuadrat memotong sumbu X di dua titik berbeda.

Contoh representasi fungsi kuadrat atau parabola

Mari kita lihat cara merepresentasikan fungsi kuadrat pada grafik menggunakan sebuah contoh.

Grafik fungsi berikut:

$f(x)=x^2-4x+5$

Hal pertama yang harus dilakukan adalah menghitung titik puncak parabola. Untuk melakukan ini, kami menggunakan rumus yang kami lihat di atas:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2$

Setelah kita mengetahui di mana titik puncaknya, kita perlu membuat tabel nilai: Kita menghitung nilai fungsi pada titik puncak dan titik-titik di sekitarnya:

$f(x)=x^2-4x+5$

$x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2$

$x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2$

$x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5$

$x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}$

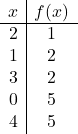
Anda juga dapat menghitung titik potong fungsi kuadrat dengan sumbu Cartesian untuk menggambar parabola dengan lebih baik, namun hal ini tidak sepenuhnya diperlukan.

Kami sekarang mewakili titik-titik yang diperoleh pada grafik :

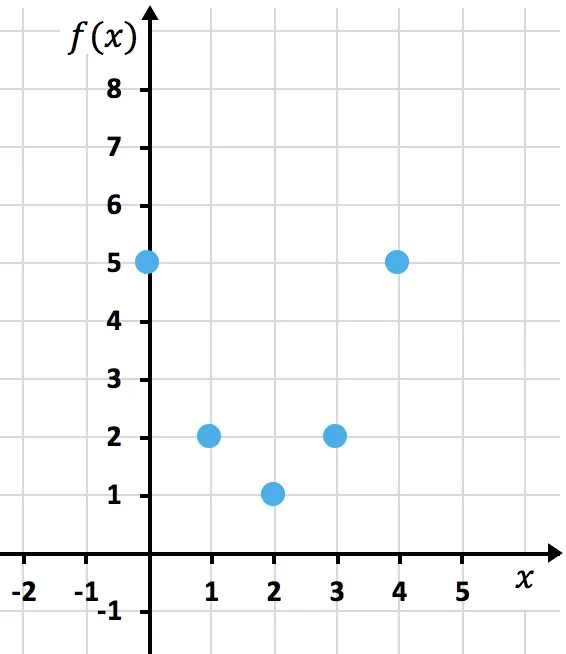
contoh cara merepresentasikan fungsi kuadrat atau parabola

Dan terakhir, kita gabungkan titik-titik tersebut membentuk parabola. Kemudian kita memanjangkan cabang-cabang parabola untuk menunjukkan bahwa ia berlanjut ke atas:

representasi fungsi kuadrat atau parabola

Latihan soal fungsi kuadrat

Latihan 1

Tentukan titik puncak fungsi kuadrat berikut:

$f(x)=2x^2+8x+4$

Lihat solusinya

Kita hitung terlebih dahulu koordinat X titik tersebut dengan menggunakan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2$

Dan sekarang kita menghitung koordinat lainnya dengan mengevaluasi fungsi di titik tersebut:

$\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}$

Oleh karena itu, titik puncak fungsi kuadrat adalah:

$\bm{(-2,-4)}$

Latihan 2

Temukan titik potong fungsi berikut dengan sumbu:

$f(x)=x^2-4x+3$

Lihat solusinya

Untuk menghitung titik potong dengan sumbu Y, kita perlu melakukan perhitungan

$f(0):$

$f(0)=0^2-4\cdot 0+3 = 3$

Oleh karena itu, fungsi tersebut melalui sumbu Y di titik:

$\bm{(0,3)}$

Dan untuk mencari titik potong dengan sumbu X kita perlu menyelesaikannya

$f(x)=0:$

$f(x)=x^2-4x+3$

$0=x^2-4x+3$

Kita menghitung akar-akar persamaan kuadrat dengan rumus:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}$

Oleh karena itu, fungsinya memotong sumbu X di dua titik:

$\bm{(1,0) \qquad (3,0)}$

Latihan 3

Gambarkan fungsi kuadrat berikut:

$f(x)=-x^2+4x+1$

Lihat solusinya

Ini adalah fungsi kuadrat. Oleh karena itu, untuk menyatakannya harus terlebih dahulu menghitung absis titik sudut parabola dengan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2$

Sekarang kita membuat tabel nilai. Untuk melakukan ini, kami menghitung nilai

$f(x)$

di atas dan di sekitar atas:

$x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5$

$x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4$

$x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4$

$x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1$

$x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}$

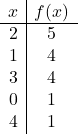
Dan terakhir, kita plot titik-titik pada grafik dan menggambar parabola:

Latihan 4

Gambarkan fungsi kuadrat berikut:

$f(x)=-2x^2-8x-1$

Lihat solusinya

Ini adalah fungsi urutan kedua. Oleh karena itu, untuk menyatakannya harus dicari terlebih dahulu absis titik puncak parabola dengan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2$

Sekarang kita membuat tabel nilai. Untuk melakukan ini, kami menghitung nilai

$f(x)$

di atas dan di sekitar atas:

$x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7$

$x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5$

$x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5$

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1$

$x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}$

Terakhir, kita plot titik-titik pada grafik dan menggambar parabola:

latihan diselesaikan langkah demi langkah fungsi kuadrat

Latihan 5

Gambarlah fungsi kuadrat tidak lengkap berikut pada suatu grafik:

$f(x)=x^2+2$

Lihat solusinya

Ini adalah fungsi polinomial derajat dua. Oleh karena itu, untuk menyatakannya harus terlebih dahulu menghitung absis titik sudut parabola dengan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0$

Dalam hal ini, fungsinya tidak lengkap karena tidak mempunyai suku derajat pertama. Untuk itu

$b=0 .$

Sekarang kita membuat tabel nilai. Untuk melakukan ini, kami menghitung nilai

$f(x)$

di atas dan di sekitar atas:

$x= 0 \ \longrightarrow \ f(0)=0^2+2=2$

$x= 1 \ \longrightarrow \ f(1)=1^2+2=3$

$x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3$

$x= 2 \ \longrightarrow \ f(2)=2^2+2=6$

$x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}$

Terakhir, kita plot titik-titik pada grafik dan menggambar parabola:

latihan yang diselesaikan untuk mewakili fungsi kuadrat yang tidak lengkap

Latihan 6

Selesaikan soal berikut yang berkaitan dengan fungsi kuadrat:

Biaya produksi suatu produk ditentukan oleh fungsi berikut:

$f(x)=x^2-12x+76$

Emas

$x$

adalah unit yang diproduksi (dalam ribuan) dan

$f(x)$

adalah biaya produksi unit (dalam ribuan euro).

Mewakili fungsi biaya produksi pada grafik.
Tentukan berapa ribu unit yang harus diproduksi untuk meminimalkan biaya.

Lihat solusinya

Ini adalah fungsi kuadrat. Oleh karena itu, untuk menyatakannya harus dicari terlebih dahulu absis titik puncak parabola dengan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6$

Sekarang kita membuat tabel nilai. Untuk melakukan ini, kami menghitung nilai

$f(x)$

di atas dan di sekitar atas:

$x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40$

$x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41$

$x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41$

$x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44$

$x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44$

$\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}$

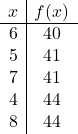
Sekarang kita plot titik-titik pada grafik dan menggambar parabola:

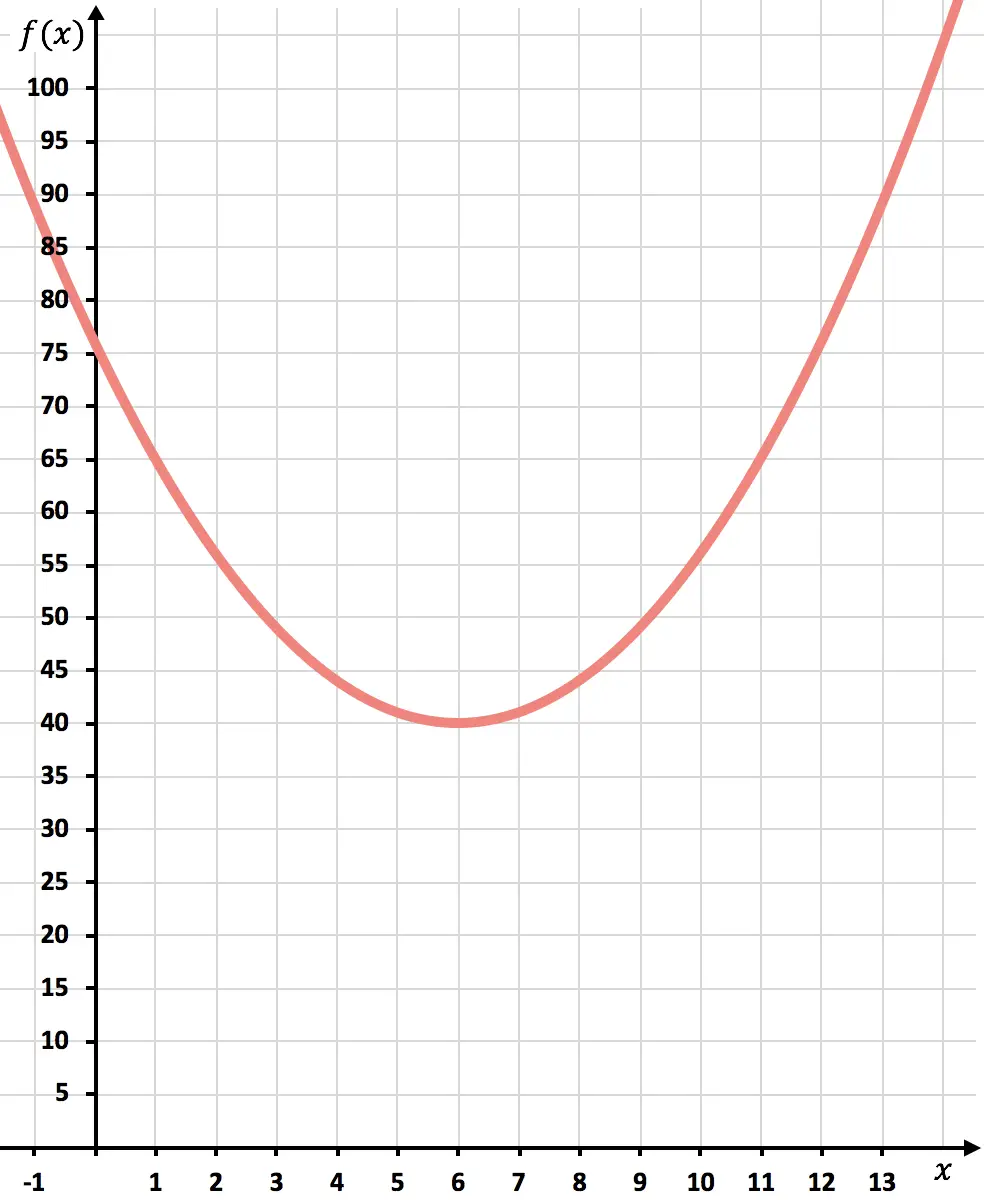
Setelah fungsinya direpresentasikan, kita akan melihat seberapa besar biaya yang diminimalkan.

Seperti yang ditunjukkan grafik, biaya minimum akan tercapai di puncak parabola. Karena di situlah fungsinya mengambil nilai terkecil.

Kesimpulannya, biaya akan diminimalkan dengan memproduksi 6.000 unit.

Latihan 7

Selesaikan soal fungsi kuadrat berikut:

Seorang atlet melakukan lempar lembing yang lintasannya dapat direpresentasikan dengan fungsi sebagai berikut:

$h(x) = -0,025x^2+2x+2$

Emas

$x$

adalah meteran yang ditutupi oleh lembing dan

$h$

tingginya (juga dalam meter).

Berapakah tinggi maksimum yang dapat dicapai lembing tersebut?

Lihat solusinya

Ini merupakan fungsi kuadrat, sehingga lintasan lembingnya berbentuk parabola.

Selain itu, karena koefisien suku kuadratnya negatif (-0,025), parabola akan berbentuk U terbalik dan cabang-cabangnya mengarah ke bawah. Dengan demikian lembing akan mencapai ketinggian maksimum di puncaknya, karena ini akan menjadi titik tertinggi parabola.

Oleh karena itu kita menghitung absis titik puncak parabola dengan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40$

Lalu kita menghitung seberapa tinggi lembing pada titik tersebut dengan mengevaluasi fungsi di dalamnya

$x=40:$

$h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42$

Oleh karena itu, ketinggian maksimum yang dapat dicapai lembing adalah 42 meter.

Latihan 8

Selesaikanlah soal fungsi kuadrat berikut ini:

Biaya produksi (dalam euro) suatu perusahaan ditentukan oleh fungsi berikut:

$C(q)=40000+20q+q^2$

Emas

$q$

adalah unit yang diproduksi.

Dan harga jual setiap unitnya adalah €520.

Berapa keuntungan yang diperoleh perusahaan jika menjual 150 unit?
Berapa unit yang harus dijual untuk mendapatkan keuntungan maksimal?

Lihat solusinya

Perusahaan memperoleh €520 untuk setiap unit yang terjual. Oleh karena itu, fungsi yang mendefinisikan pendapatan adalah:

$I(q)=520\cdot q = 520q$

Emas

$q$

adalah unit yang terjual.

Tapi mereka bertanya kepada kita tentang keuntungan, yaitu pendapatan dikurangi biaya. Oleh karena itu, kami mengurangkan pendapatan dikurangi biaya untuk mendapatkan fungsi yang menggambarkan laba perusahaan:

$B(q)=I(q)-C(q)$

$B(q)=520q - (40000+20q+q^2)$

$B(q)=520q - 40000-20q-q^2$

$B(q)=-q^2 + 500q - 40000$

Setelah kita mengetahui fungsi yang menggambarkan keuntungan perusahaan, cukup substitusikan 150 ke dalam persamaan fungsi tersebut untuk menghitung keuntungan yang diperoleh perusahaan dengan menjual 150 unit:

$\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}$

Jadi, dengan menjual 150 unit, perusahaan akan memperoleh keuntungan sebesar €12.500.

Pernyataan tersebut juga meminta kita menghitung berapa unit keuntungan maksimal yang dicapai.

Fungsi yang menggambarkan keuntungan merupakan fungsi kuadrat, sehingga berbentuk parabola. Dan karena koefisien suku kuadratnya negatif (-1), parabola akan berbentuk U terbalik dan cabang-cabangnya mengarah ke bawah. Oleh karena itu, perolehan maksimum akan diperoleh di bagian atas, karena ini adalah titik tertinggi parabola.

Oleh karena itu kita menghitung absis titik puncak parabola dengan rumus:

$x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250$

Jadi perusahaan akan memperoleh keuntungan maksimal dengan menjual 250 unit.

Sebaliknya, meski siaran pers tidak menanyakannya, kita bisa menentukan keuntungan yang didapat dengan menjual 250 unit ini:

$B(250) =-(250)^2 + 500\cdot250- 40000= 22500$

€

Fungsi kuadrat atau parabola

Apa itu fungsi kuadrat?

Kecekungan dan konveksitas suatu fungsi kuadrat

Titik puncak fungsi kuadrat

Titik potong dengan sumbu fungsi kuadrat

Contoh representasi fungsi kuadrat atau parabola

Latihan soal fungsi kuadrat

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Latihan 6

Latihan 7

Latihan 8

Tinggalkan Komentar Batalkan Balasan