Fungsi linier dan fungsi affine -

Pada artikel ini Anda akan menemukan penjelasan tentang fungsi affine dan fungsi linier, serta perbedaan yang ada antara kedua jenis fungsi tersebut. Selain itu, Anda akan melihat contoh cara membuat grafik fungsi affine dan fungsi linier serta cara menghitung ekspresi keduanya dari dua titik. Terakhir, Anda akan dapat berlatih dengan beberapa latihan yang diselesaikan selangkah demi selangkah.

Apa yang dimaksud dengan fungsi affine dan fungsi linier?

Pengertian fungsi affine dan fungsi linier adalah sebagai berikut:

Fungsi affine adalah fungsi polinomial derajat pertama, yaitu fungsi yang digambarkan dalam grafik berupa garis lurus. Fungsi terkait adalah sebagai berikut:

$f(x)=mx+n$

Emas

$m$

adalah kemiringan garis dan

$n$

Ini adalah perpotongan y, yaitu tempat fungsi tersebut memotong sumbu vertikal.

Dalam matematika, fungsi affine disebut juga transformasi linier dalam konteks aljabar linier.

Fungsi linier adalah fungsi affine yang tidak mempunyai suku bebas. Oleh karena itu, rumus fungsi linier adalah:

$f(x)=mx$

Emas

$m$

adalah kemiringan garis.

Domain dan jangkauan (atau rentang) fungsi linier dan fungsi affine semuanya bilangan real:

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

Apa perbedaan antara fungsi linier dan fungsi affine?

Sekarang setelah Anda melihat konsep fungsi linier dan fungsi affine, Anda akan menyadari bahwa keduanya sangat mirip satu sama lain. Namun, perbedaan di antara keduanya berikut ini sangat penting:

Satu-satunya perbedaan antara fungsi linier dan fungsi affine adalah bahwa fungsi linier tidak memiliki suku bebas sedangkan fungsi affine selalu memiliki koefisien titik potong (n) yang berbeda dari nol (0).

Fungsi linear

$f(x)=mx$

fungsi linear

$f(x)=mx+n$

Artinya suatu fungsi linier selalu melalui titik asal koordinat , titik (0,0). Sebaliknya, fungsi affine tidak akan pernah melewati titik ini karena mempunyai intersep selain 0.

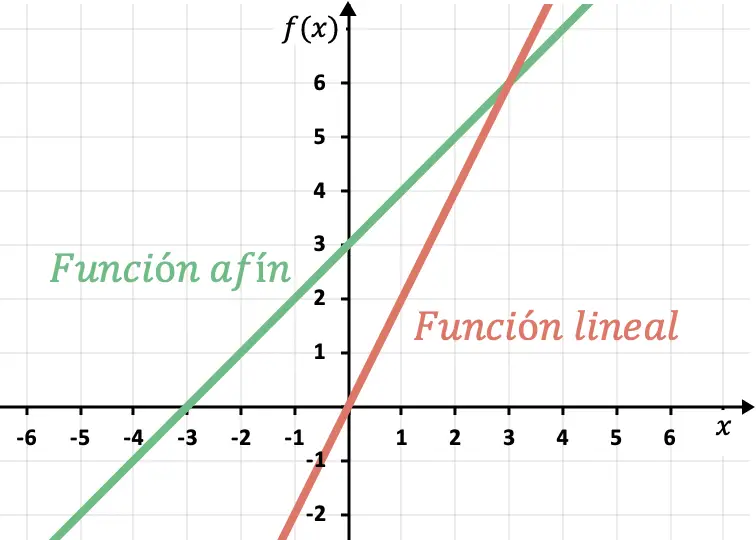
Apa perbedaan antara fungsi linier dan fungsi affine?

Kemiringan dan perpotongan y dari fungsi linier atau afin

Pada bagian ini, kita akan menganalisis contoh fungsi affine atau linier untuk memahami arti istilah-istilahnya

$m$

Dan

$n$

, atau dengan kata lain, kemiringan dan perpotongan y.

Tentukan ekspresi fungsi yang ditunjukkan pada grafik dan klasifikasikan ke dalam fungsi linier atau afin.

Jenis fungsi ini mengikuti ekspresi berikut:

$f(x)=mx+n$

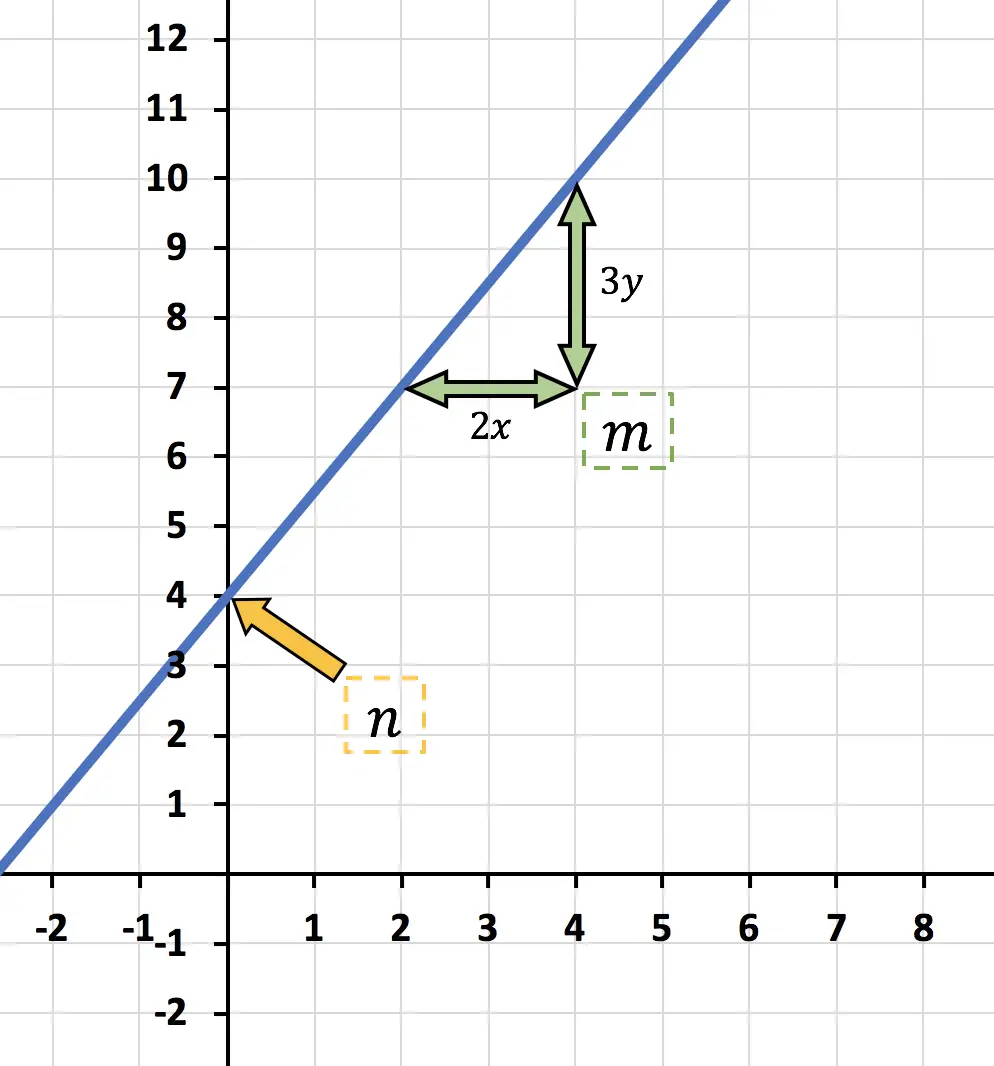
artinya kemiringan dan perpotongan y fungsi linier atau afin m dan n

$n$

Ini adalah perpotongan y, yaitu ketika fungsi tersebut memotong sumbu Y vertikal. Jadi dalam hal ini:

$n=4$

Di sisi lain,

$m$

adalah kemiringan garis. Y dapat dihitung dengan membagi selisih y antara dua titik dengan selisih x antara dua titik yang sama:

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$

mengatakan “berapa banyak y bertambah untuk setiap x” , jadi dalam hal ini fungsinya “3y bertambah untuk setiap 2x” .

Kesimpulannya, ekspresi fungsi affine yang direpresentasikan dalam grafik adalah:

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

Selain itu, karena titik potong y bukan nol, maka ini merupakan fungsi affine .

Di bawah ini kami tunjukkan lebih banyak contoh fungsi linier dan affine untuk melengkapi pemahaman Anda:

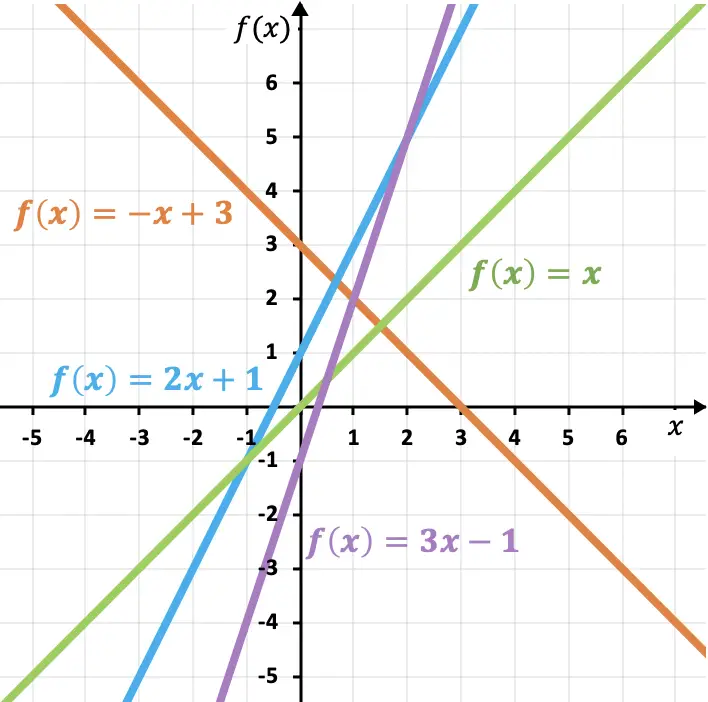
Seperti yang dapat Anda lihat pada contoh berikut, semakin besar kemiringannya, semakin curam garisnya, dan oleh karena itu, semakin besar pula fungsinya. Demikian pula, koefisien kemiringan menentukan naik atau turunnya suatu fungsi:

Jika kemiringannya positif, maka fungsinya meningkat , yaitu meningkat seiring bertambahnya x .
Jika kemiringannya negatif, fungsinya menurun , yaitu menurun seiring bertambahnya x .

Selain itu, Anda juga dapat mengetahui apakah dua garis sejajar atau tegak lurus berdasarkan kemiringannya:

Jika dua garis memiliki kemiringan yang sama, maka keduanya sejajar , yaitu tidak berpotongan di titik mana pun atau identik sepenuhnya.

$m_1 = m_2$

Sebaliknya, dua garis tegak lurus , artinya berpotongan membentuk sudut vertikal (90º), jika kemiringannya sesuai dengan hubungan berikut:

$m_1 = -\cfrac{1}{m_2}$

Contoh representasi fungsi affine atau linier

Mari kita lihat cara membuat grafik fungsi derajat pertama menggunakan sebuah contoh.

Gambarkan fungsi affine berikut:

$f(x)=2x-1$

Hal pertama yang perlu kita lakukan adalah membuat array nilai. Untuk melakukan ini, kami memberikan nilai yang kami inginkan

$x$

untuk mendapatkan nilai

$f(x)$

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

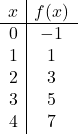
Meskipun tabel nilai dengan dua poin sudah cukup, kita dapat melakukan lebih banyak poin untuk memastikan kebenarannya.

Setelah kita membuat tabel nilai, kita memplot titik-titik pada grafik:

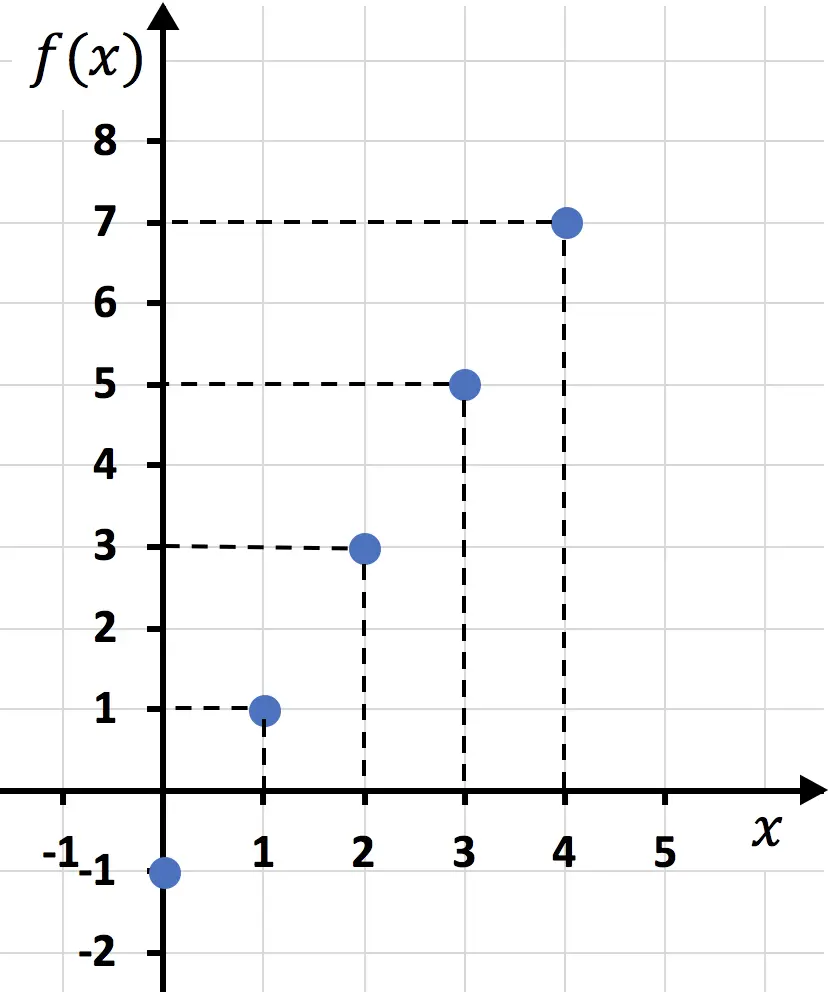
cara merepresentasikan garis atau fungsi linier atau dan affine

Dan terakhir, kita gabungkan titik-titik tersebut dan buat garis:

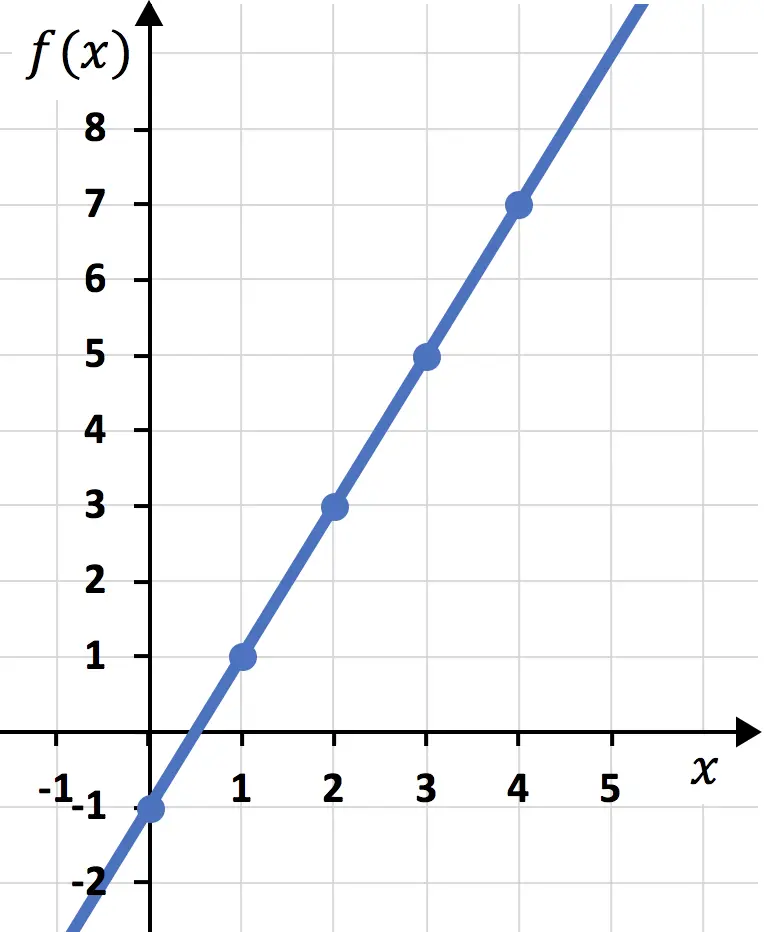
representasi grafis dari fungsi linier atau affine

Dan dengan cara ini, kita telah merepresentasikan fungsi tersebut pada grafik. Seperti yang Anda lihat, tidak rumit, Anda hanya perlu membuat tabel nilai terlebih dahulu, lalu memplot titik-titiknya pada grafik.

Cara menghitung fungsi linier atau affine dari dua titik

Sekarang mari kita lihat cara mencari fungsi linier atau affine dari dua titik menggunakan contoh:

Hitung fungsi linier yang memenuhi
$f(3)=5$

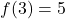
dan melalui intinya

$(1,-1).$

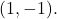
Pertama,

$f(3)=5$

Artinya fungsi tersebut melewati suatu titik

$(3,5)$

Oleh karena itu, karena kita mempunyai dua titik yang dilalui fungsi tersebut, kita dapat menghitung kemiringannya

$m$

fungsi:

Dengan mempertimbangkan dua hal,

$P_1=(x_1,y_1)$

Dan

$P_2=(x_2,y_2)$

, kemiringan

$m$

fungsi dihitung:

$m=\cfrac{y_2-y_1}{x_2-x_1}$

Dalam kasus kita, fungsinya melewati titik-titik

$(3,5)$

Dan

$(1,-1)$

. Jadi kemiringannya

$m$

dari fungsinya adalah:

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

Oleh karena itu fungsinya akan berbentuk:

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

Begitu kita tahu

$m$

kita bisa memecahkan misterinya

$n$

. Untuk melakukan ini, kita substitusikan koordinat titik yang termasuk dalam fungsi tersebut ke dalam persamaan. Misalnya poin (3.5):

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

Kami memecahkan persamaan yang dihasilkan:

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

Oleh karena itu, fungsi liniernya adalah:

$\bm{f(x)=3x-4}$

Latihan soal fungsi linear dan affine

Latihan 1

Tentukan kemiringan dan titik asal fungsi affine berikut:

$f(x)=-5x-2$

Lihat solusinya

Fungsi linier memiliki bentuk

$f(x)=mx+n .$

Oleh karena itu, kemiringan fungsi tersebut adalah bilangan yang menyertai x , yang dalam hal ini adalah -5:

$\bm{m=-5}$

Dan titik potong y adalah suku bebas, yang dalam hal ini adalah -2:

$\bm{n=-2}$

Latihan 2

Gambarkan fungsi affine berikut:

$f(x)=x+1$

Lihat solusinya

Kita beri nilai dulu

$x$

untuk membuat tabel nilai:

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

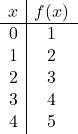
Dan kemudian kita mewakili titik-titik dari tabel nilai pada grafik dan menggambar garis:

Latihan 3

Plot fungsi affine berikut pada grafik:

$f(x)=-2x+6$

Lihat solusinya

Kita beri nilai dulu

$x$

untuk membuat tabel nilai:

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

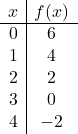
Dan terakhir kami mewakili titik-titik dari tabel nilai pada grafik dan menggambar garis:

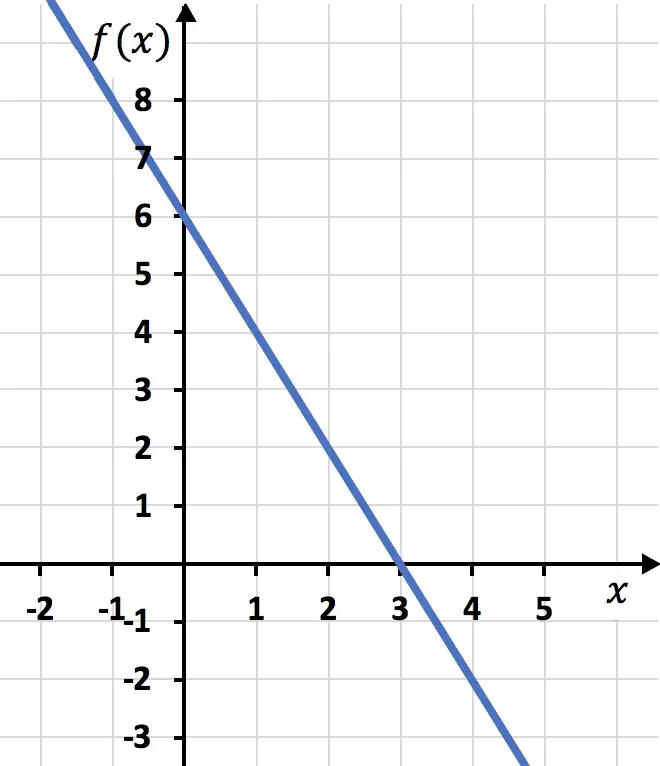
latihan diselesaikan langkah demi langkah fungsi linier dan affine

Latihan 4

Tentukan ekspresi fungsi affine yang melalui titik (2,3) dan (0,1).

Lihat solusinya

Fungsi tersebut melalui titik (2,3) dan (0,1), sehingga kemiringan fungsinya adalah:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

Dan fungsinya akan berbentuk:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

Setelah kita mengetahui m, kita dapat menghitung n . Untuk melakukan ini, kita perlu mensubstitusikan koordinat titik yang termasuk dalam fungsi tersebut ke dalam persamaan. Misalnya poin (2,3):

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$

$3=2+n$

Kita sekarang harus menyelesaikan persamaan yang dihasilkan:

$3-2=n$

$1 = n$

Oleh karena itu, fungsinya sesuai dengan ekspresi berikut:

$\bm{f(x)=x+1}$

Latihan 5

Gambarkan fungsi affine berikut:

$f(x)=2x-1$

Lihat solusinya

Kita beri nilai dulu

$x$

untuk membuat tabel nilai:

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

Dan kemudian kita mewakili titik-titik dari tabel nilai pada grafik dan menggambar garis:

Latihan yang diselesaikan untuk membuat grafik fungsi linier atau affine

Latihan 6

Hitung fungsi linier yang memenuhi dua kondisi berikut:

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

Lihat solusinya

Semoga itu menjadi kenyataan

$f(3)=-2$

Artinya fungsi tersebut melalui titik (3,-2). Dan, dengan cara yang sama,

$f(-1)=6$

Artinya fungsi tersebut melalui titik (-1.6).

Jadi fungsi tersebut melewati titik (3,-2) dan (-1,6), sehingga kemiringannya adalah:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

Oleh karena itu fungsinya akan berbentuk:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

Dan begitu kita mengetahui m, kita dapat menghitung n . Untuk melakukan ini, kita substitusikan koordinat titik yang termasuk dalam fungsi tersebut ke dalam persamaan. Misalnya poin (3,-2):

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

Dan kami menyelesaikan persamaan yang dihasilkan:

$-2=-6+n$

$-2+6=n$

$4 = n$

Oleh karena itu fungsinya adalah:

$\bm{f(x)=-2x+4}$

Latihan 7

Temukan fungsi affine yang dijalankannya

$f(1) =6$

dan melewati titik (3.5).

Lihat solusinya

Semoga itu menjadi kenyataan

$f(1)=6$

Artinya fungsi tersebut melalui titik (1,6).

Oleh karena itu, fungsi tersebut melalui titik (1.6) dan (3.5) sehingga kemiringannya adalah:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

Oleh karena itu fungsinya akan berbentuk:

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

Setelah kita mengetahui suku m kita dapat menghitung koefisien n . Untuk melakukan ini, kita substitusikan koordinat titik yang termasuk dalam fungsi tersebut ke dalam persamaan. Misalnya poin (1,6):

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

Kami memecahkan persamaan yang dihasilkan:

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

Ingatlah bahwa untuk menjumlahkan pecahan, Anda harus terlebih dahulu mereduksinya menjadi penyebut yang sama, lalu menjumlahkan pembilangnya:

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

Oleh karena itu fungsinya adalah:

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

Latihan 8

Selesaikan masalah berikut yang berkaitan dengan fungsi linier dan affine:

Sebuah toko menjual 40 unit produk ketika harganya €15/unit, dan 65 unit ketika harganya €10/unit.

Hitung fungsi permintaan untuk produk tersebut, dengan asumsi itu adalah fungsi affine.
Berapa unit yang akan terjual jika harga ditetapkan €12/unit?

Lihat solusinya

Karena ini adalah fungsi affine, maka fungsinya akan bertipe

$f(x)=mx+n .$

Emas

$x$

akan menjadi harga satuan produk dan

$f(x)$

akan menjadi unit yang terjual.

Siaran pers memberitahu kita bahwa ketika harga €15/unit, 40 unit terjual. Oleh karena itu, sebagai

$x$

adalah harga dan

$f(x)$

unit terjual, kesetaraan berikut harus dihormati:

$f(15)=40$

Dan ketika harganya €10/unit, 65 unit terjual. Jadi, dengan menggunakan alasan yang sama:

$f(10)=65$

Semoga itu menjadi kenyataan

$f(15)=40$

Artinya fungsi tersebut melalui titik (15.40). DAN

$f(10)=65$

Artinya fungsi tersebut melalui titik (10.65).

Oleh karena itu kemiringan fungsinya adalah:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

Oleh karena itu fungsinya akan berbentuk:

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

Setelah kita mengetahui m, kita dapat menghitung n . Untuk melakukan ini, kita substitusikan koordinat titik yang termasuk dalam fungsi tersebut ke dalam persamaan. Misalnya intinya (15:40):

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$