Fungsi kosinus hiperbolik

Di sini Anda akan menemukan segala sesuatu tentang fungsi kosinus hiperbolik: apa rumusnya, representasi grafisnya, karakteristiknya, hubungan matematisnya dengan fungsi lain, dll.

Rumus kosinus hiperbolik

Fungsi kosinus hiperbolik adalah salah satu fungsi hiperbolik utama dan diwakili oleh simbol cosh(x) . Kosinus hiperbolik sama dengan jumlah e ^x ditambah e ^-x dibagi 2.

Oleh karena itu, rumus kosinus hiperbolik adalah:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

Jadi, kosinus hiperbolik secara matematis berhubungan dengan fungsi eksponensial. Di tautan berikut Anda dapat melihat properti dari jenis fungsi ini:

➤ Lihat: sifat-sifat fungsi eksponensial

Representasi grafis dari kosinus hiperbolik

Representasi grafis dari fungsi kosinus hiperbolik berbentuk fungsi kuadrat (atau parabola):

➤ Lihat: Representasi grafis dari fungsi kuadrat .

Pada grafik ini terlihat jelas bahwa kosinus hiperbolik merupakan fungsi genap karena simetris terhadap sumbu y.

Sebaliknya, grafik kosinus hiperbolik sangat berbeda dengan grafik kosinus (fungsi trigonometri) yang merupakan fungsi periodik. Gambaran grafis cosinus dan segala perbedaannya dengan cosinus hiperbolik dapat Anda lihat pada link berikut:

➤ Lihat: representasi grafis dari fungsi kosinus

Ciri-ciri kosinus hiperbolik

Kosinus hiperbolik memperhatikan sifat-sifat berikut:

Domain fungsi kosinus hiperbolik adalah semua bilangan real:

$\text{Dom } f = \mathbb{R}$

Sebaliknya, rentang (atau rentang) fungsi kosinus hiperbolik adalah 1 dan semua bilangan lebih besar dari 1:

$\text{Im } f= [1,+\infty)$

Kosinus hiperbolik adalah fungsi kontinu dan genap.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

Fungsi tersebut memotong sumbu Y di titik x=0.

$(0,1)$

Sebaliknya, fungsi tersebut tidak mempunyai titik potong dengan sumbu X.

Dua limit hingga tak terhingga (positif dan negatif) dari fungsi kosinus hiperbolik menghasilkan plus tak terhingga.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

Kosinus hiperbolik mengecil hingga x = 0 dan sejak titik tersebut bertambah hingga tak terhingga, sehingga fungsinya mempunyai minimum di x = 0.

$(0,1)$

Fungsinya cembung di seluruh domainnya, sehingga tidak mempunyai titik belok.

Turunan dari fungsi kosinus hiperbolik adalah sinus hiperbolik:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

Integral fungsi kosinus hiperbolik adalah sinus hiperbolik:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

Polinomial Taylor (atau deret Maclaurin) dari fungsi kosinus hiperbolik adalah sebagai berikut:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

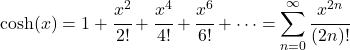
Transformasi Laplace dari fungsi kosinus hiperbolik adalah sebagai berikut:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Hubungan matematis kosinus hiperbolik

Selanjutnya, kita akan melihat bagaimana kosinus hiperbolik dapat dihitung dari fungsi hiperbolik lainnya, karena semuanya berhubungan secara matematis.

Persamaan dasar menghubungkan kosinus hiperbolik dengan sinus hiperbolik:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Lihat: sinus hiperbolik

Tiga fungsi hiperbolik utama (sinus hiperbolik, kosinus, dan tangen) dapat dihubungkan dengan persamaan berikut:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Sebaliknya, kosinus hiperbolik dari penjumlahan (atau pengurangan) dua bilangan berbeda dapat ditentukan dengan rumus berikut:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

Kosinus hiperbolik dua kali suatu bilangan sama dengan jumlah kuadrat kosinus hiperbolik dan sinus hiperbolik bilangan ini:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

Penjumlahan atau pengurangan dua kosinus hiperbolik dapat dihitung dengan menggunakan rumus berikut:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Terakhir, kuadrat kosinus hiperbolik dapat dihitung dengan rumus berikut:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Rumus kosinus hiperbolik

Representasi grafis dari kosinus hiperbolik

Ciri-ciri kosinus hiperbolik

Hubungan matematis kosinus hiperbolik

Tinggalkan Komentar Batalkan Balasan