Kecekungan dan konveksitas suatu fungsi (kelengkungan)

Di sini Anda akan mempelajari apa itu kecekungan dan kecembungan suatu fungsi dan cara mengetahui apakah suatu fungsi cekung atau cembung. Selain itu, Anda akan dapat berlatih dengan latihan langkah demi langkah tentang kelengkungan suatu fungsi.

Berapakah kecekungan dan kecembungan suatu fungsi?

Kecekungan dan konveksitas suatu fungsi mengacu pada kelengkungan grafik suatu fungsi. Fungsi cekung adalah fungsi yang grafiknya berbentuk gunung, dan fungsi cembung adalah fungsi yang grafiknya berbentuk lembah.

Pada paragraf sebelumnya, fungsi cekung dan fungsi cembung telah didefinisikan secara informal untuk memudahkan pemahaman, namun definisi matematis dari fungsi cekung dan fungsi cembung adalah sebagai berikut:

  • Fungsi cekung: bila ruas yang menghubungkan dua titik mana pun dari fungsi tersebut berada di bawah kurva.
  • Fungsi cembung: bila ruas yang menghubungkan dua titik mana pun dari fungsi tersebut berada di atas kurva.
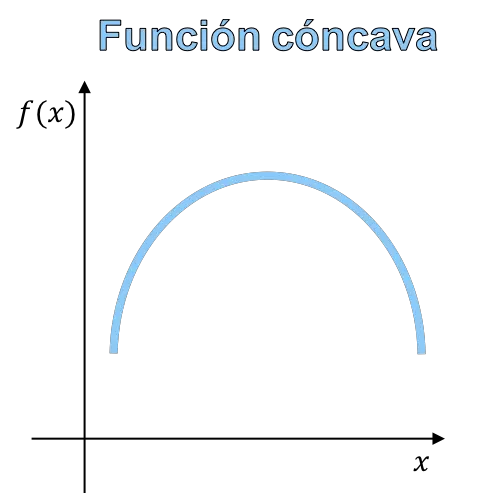
fungsi cekung
fungsi cembung

Pada akhirnya, perbedaan antara fungsi cekung dan fungsi cembung terletak pada bentuk fungsinya sehingga, Anda dapat membedakan kecekungan dan kecembungan dari grafik fungsinya.

Namun, suatu fungsi tidak harus cekung atau cembung pada seluruh domainnya, tetapi bisa juga cekung pada satu interval dan cembung pada interval lainnya.

Catatan: Komunitas matematika masih belum sepenuhnya setuju dan, oleh karena itu, beberapa profesor mengatakan sebaliknya: mereka menyebut suatu fungsi cekung yang berbentuk a

\bm{\cup}

, dan fungsi cembung yang berbentuk

\bm{\cap}

. Pokoknya yang penting tahu apa fungsinya, apapun namanya.

Cara mempelajari kelengkungan suatu fungsi

Mempelajari kelengkungan suatu fungsi melibatkan pencarian kecekungan dan kecembungan suatu fungsi, yaitu mengetahui interval di mana fungsi tersebut cekung dan interval di mana fungsi tersebut cembung.

Jadi, untuk mempelajari kelengkungan suatu fungsi, harus dilakukan langkah-langkah sebagai berikut:

  1. Temukan titik-titik yang tidak termasuk dalam domain fungsi tersebut.
  2. Hitung turunan pertama dan turunan kedua fungsi tersebut.
  3. Temukan akar-akar turunan kedua , yaitu menghitung titik-titik yang menghilangkan turunan kedua dengan menyelesaikannya

    f''(x)=0

    .

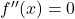
  4. Buatlah interval dengan akar-akar turunan dan titik-titik yang tidak termasuk dalam domain fungsi tersebut.
  5. Hitung nilai turunan kedua pada suatu titik pada setiap interval.
  6. Jadi, tanda turunan kedua menentukan kecekungan atau kecembungan suatu fungsi pada interval ini:
    • Jika turunan kedua dari fungsi tersebut positif, maka fungsi tersebut cembung pada interval tersebut.
    • Jika turunan kedua dari fungsi tersebut negatif, maka fungsi tersebut cekung pada interval tersebut.

Contoh cara mencari kelengkungan suatu fungsi

Selanjutnya, kita akan menyelesaikan contoh langkah demi langkah sehingga Anda dapat melihat bagaimana interval kecekungan dan kecembungan suatu fungsi dihitung.

  • Pelajari kecekungan dan kecembungan fungsi berikut:

f(x)=x^3-3x

Hal pertama yang harus dilakukan adalah menghitung domain definisi fungsi. Dalam hal ini, kita mempunyai fungsi polinomial, sehingga domain dari fungsi tersebut terdiri dari bilangan real:

\text{Dom } f= \mathbb{R}

Setelah kita menghitung domain dari fungsi tersebut, kita perlu menyelidiki pada titik mana turunan kedua dari fungsi tersebut hilang.

Oleh karena itu kami menghitung turunan pertama dari fungsi tersebut:

f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3

Selanjutnya kita mencari turunan kedua dari fungsi tersebut:

f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x

Dan sekarang kita menetapkan turunan kedua sama dengan 0 dan menyelesaikan persamaan:

f''(x)=0

6x=0

x=\cfrac{0}{6}

x=0

Setelah kita menghitung domain dari fungsi dan

f''(x)=0

, kami mewakili semua titik kritis yang ditemukan di garis. Dalam hal ini kami tidak menemukan titik kritis dalam perhitungan domain definisi fungsi, tetapi kami memperoleh titik yang membatalkan turunan kedua fungsi tersebut:

Dan sekarang kita evaluasi tanda turunan keduanya pada setiap interval, untuk mengetahui apakah fungsinya cekung atau cembung. Oleh karena itu, kita mengambil sebuah titik pada setiap interval (tidak pernah titik kritisnya) dan melihat tanda apa yang dimiliki turunan kedua pada titik tersebut:

f''(x)=6x

f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}

f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}

Terakhir, kami menyimpulkan interval kecekungan dan kecembungan fungsi tersebut. Jika turunan keduanya positif berarti fungsinya cembung.

(\bm{\cup})

, dan jika turunan keduanya negatif berarti fungsinya cekung

(\bm{\cap})

. Jadi interval kecekungan dan kecembungan fungsi tersebut adalah:

Cembung

(\bm{\cup})

:

\bm{(0,+\infty)}

Cekung

(\bm{\cap})

:

\bm{(-\infty,0)}

Latihan soal kecekungan dan kecembungan suatu fungsi

Latihan 1

Hitung interval kecekungan dan kecembungan fungsi polinomial berikut:

f(x) = x^3-3x^2-2x

Fungsi dalam latihan ini adalah polinomial, sehingga domain dari fungsi tersebut terdiri dari bilangan real:

\text{Dom } f= \mathbb{R}

Setelah menentukan domain suatu fungsi, kita bedakan:

f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2

Selanjutnya kita mencari turunan kedua dari fungsi tersebut:

f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6

Dan sekarang kita menetapkan turunan kedua sama dengan 0 dan menyelesaikan persamaan:

f''(x)= 0

6x-6= 0

6x= 6

x= \cfrac{6}{6}

x=1

Setelah kita menghitung domain dari fungsi tersebut dan menyelesaikannya

f''(x)=0

, kami mewakili semua titik tunggal yang ditemukan pada garis bilangan:

Dan sekarang mari kita ambil suatu titik yang termasuk dalam setiap interval dan lihat tanda apa yang memiliki turunan kedua pada titik ini:

f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}

f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}

Jika turunan keduanya lebih besar dari nol berarti fungsinya cembung.

(\bm{\cup})

, tetapi bila turunan keduanya negatif berarti fungsinya cekung

(\bm{\cap})

. Oleh karena itu, interval kecekungan dan kecembungan adalah:

Cembung

(\bm{\cup})

:

\bm{(1,+\infty)}

Cekung

(\bm{\cap})

:

\bm{(-\infty,1)}

Latihan 2

Pelajari kelengkungan fungsi rasional berikut:

\displaystyle f(x)=\frac{x^3}{x^2-4}

Pertama kita perlu menghitung domain dari fungsi tersebut. Karena ini adalah fungsi rasional, kita menetapkan penyebutnya sama dengan nol untuk melihat bilangan mana yang tidak termasuk dalam domain fungsi tersebut:

x^2-4= 0

x^2=4

\sqrt{x^2}=\sqrt{4}

x=\pm 2

Artinya jika x adalah -2 atau +2, penyebutnya adalah 0. Oleh karena itu, fungsinya tidak akan ada. Oleh karena itu, domain fungsi tersebut terdiri dari semua bilangan kecuali x=-2 dan x=+2.

\text{Dom } f= \mathbb{R}-\{-2, +2 \}

Kedua, kita menghitung turunan pertama dari fungsi tersebut:

f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}

f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}

Lalu kita selesaikan turunan keduanya:

f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}

f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }

Semua suku dikalikan dengan

(x^2-4)

. Oleh karena itu kita dapat menyederhanakan pecahan tersebut:

f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }

f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }

f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }

f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }

f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }

Sekarang mari kita hitung akar-akar turunan kedua dari fungsi tersebut:

f''(x)= 0

\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0

Syarat

\left(x^2-4\right)^3

Caranya adalah dengan membagi seluruh ruas kiri, sehingga kita dapat mengalikannya dengan seluruh ruas kanan:

8x^3+96x =0\cdot \left(x^2-4\right)^3

8x^3+96x =0

Kami mengekstrak faktor persekutuan:

x(8x^2+96)=0

Agar perkaliannya sama dengan 0, salah satu dari dua unsur perkaliannya harus nol. Oleh karena itu, kami menetapkan setiap faktor sama dengan 0:

\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}

x= \sqrt{-12}

Tidak ada penyelesaian karena tidak ada akar negatif dari bilangan real.

Sekarang kita nyatakan pada garis semua titik kritis yang diperoleh, yaitu titik-titik yang tidak termasuk dalam domain (x=-2 dan x=+2) dan titik-titik yang membatalkan turunan kedua (x=0):

Dan kita evaluasi tanda turunan keduanya pada setiap interval, untuk mengetahui apakah fungsinya cekung atau cembung. Jadi kita ambil sebuah titik di setiap interval dan lihat tanda apa yang mempunyai turunan kedua di titik tersebut:

f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}

f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}

f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}

f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}

Jika turunan keduanya positif berarti fungsinya cembung.

(\bm{\cup})

, dan jika turunan keduanya negatif berarti fungsinya cekung

(\bm{\cap})

. Oleh karena itu, interval kecekungan dan kecembungan adalah:

Cembung

(\bm{\cup})

:

\bm{(-2,0)\cup (2,+\infty)}

Cekung

(\bm{\cap})

:

\bm{(-\infty,-2)\cup (0,2)}

Latihan 3

Sebuah fungsi

f(x)

memiliki relatif ekstrim dalam

x=3

. Terlebih lagi, fungsinya cembung

(\cup )

pada titik yang sama ini. Tentukan apakah ekstrim relatifnya adalah minimum atau maksimum.

➤ Lihat: definisi maxima dan minima suatu fungsi

Biarkan fungsi cembung

(\cup)

Di dalam

x=3

berarti turunan kedua pada titik ini positif, yaitu

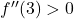f''(3)>0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”74″ style=”vertical-align: -5px;”></p> <p> .</p> <p class= Oleh karena itu, relatif ekstrim dari

\bm{x=3}

Ini adalah minimum , karena

f''(3)

Itu positif.

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top