Fungsi irasional atau fungsi radikal -

Halaman ini menjelaskan apa itu fungsi irasional disebut juga fungsi radikal, serta semua ciri-ciri dari jenis fungsi tersebut. Anda juga akan menemukan cara menghitung domain fungsi radikal atau irasional dan, sebagai tambahan, Anda akan dapat melihat cara merepresentasikannya dalam grafik dengan contoh dan latihan dengan latihan dan masalah yang diselesaikan langkah demi langkah.

Apa yang dimaksud dengan fungsi irasional (atau radikal)?

Fungsi irasional memiliki arti yang sama dengan fungsi radikal dan oleh karena itu, keduanya memiliki definisi yang sama:

Fungsi irasional , disebut juga fungsi radikal , adalah fungsi yang mempunyai variabel bebas x di bawah lambang akar.

Seperti yang sudah kita ketahui, hasil root bisa positif atau negatif. Jadi representasi fungsi irasional (atau radikal) memiliki dua kemungkinan kurva:

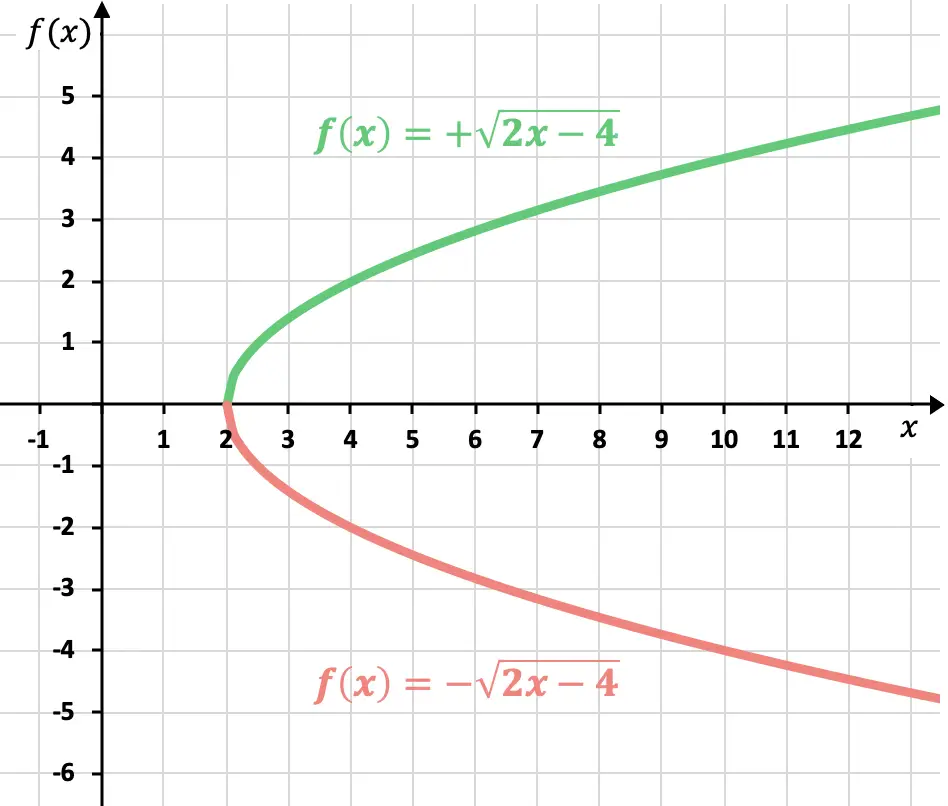
Tetapi jika tandanya tidak ditentukan, maka fungsi positif seharusnya diwakili.

Di sisi lain, fungsi irasional tidak sama dengan fungsi rasional. Meskipun keduanya memiliki nama yang sangat mirip, keduanya memiliki jenis fungsi yang sangat berbeda.

Domain fungsi irasional atau radikal

Domain suatu fungsi dengan akar bergantung pada paritas indeks akar, yaitu bergantung pada apakah indeks radikalnya genap atau ganjil.

Domain suatu fungsi dengan akar indeks genap

Seperti yang Anda ketahui, tidak ada akar (indeks genap) dari bilangan negatif. Oleh karena itu, fungsi radikal dengan indeks genap akan ada selama isinya sama dengan atau lebih besar dari 0.

Sebagai contoh, mari kita lihat bagaimana domain dari fungsi radikal atau irasional berikut dihitung:

$f(x)=\sqrt{x-4}$

Ini adalah fungsi indeks genap radikal, jadi kita harus melihat kapan isinya positif atau nol :

$x-4\ge 0$

Kami menyelesaikan pertidaksamaan:

$x\ge 4$

Jadi fungsi tersebut akan ada setiap kali x lebih besar atau sama dengan 4, dan ditunjukkan dengan interval berikut:

$\text{Dom } f= [4,+\infty)$

Domain suatu fungsi dengan akar indeks ganjil

Fungsi irasional dengan indeks ganjil tidak mempunyai masalah ini, karena akar indeks ganjil dari bilangan negatif ada:

$\sqrt[3]{-8}=-2$

Oleh karena itu, fungsi radikal dari indeks ganjil ada untuk nilai x apa pun. Atau dengan kata lain domain hanya terdiri dari bilangan real saja .

Misalnya, kita akan menghitung domain definisi fungsi radikal berikut yang indeksnya ganjil:

$f(x)=\sqrt[3]{3x-4}$

Karena merupakan fungsi irasional dengan indeks ganjil, domainnya terdiri dari bilangan real:

$\text{Dom } f= \mathbb{R}$

Bagaimana merepresentasikan fungsi yang irasional atau radikal

Mari kita lihat cara merepresentasikan fungsi dengan akar pada grafik menggunakan sebuah contoh.

Gambarkan fungsi radikal atau irasional berikut pada grafik:

$f(x)=\sqrt{x+2}$

Hal pertama yang harus dilakukan adalah mencari domain dari fungsi tersebut. Karena bilangan tersebut adalah akar kuadrat, maka apa pun yang ada di dalamnya harus positif, karena tidak ada akar kuadrat dari bilangan negatif. Oleh karena itu, fungsi radikal akan tetap ada selama kandungannya sama atau lebih besar dari 0:

$x+2\ge 0$

$x\ge -2$

Jadi, domain fungsi tersebut terdiri dari semua bilangan yang lebih besar atau sama dengan -2. Artinya:

$\text{Dom } f = [-2,+\infty)$

Setelah kita mengetahui domain fungsinya, kita membuat tabel nilai. Jelasnya, semakin banyak poin yang kita hitung, semakin tepat representasi fungsinya. Namun menghitung 3 atau 4 poin dalam interval domain sudah cukup:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

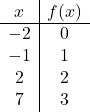
Kami sekarang mewakili titik-titik yang diperoleh pada grafik :

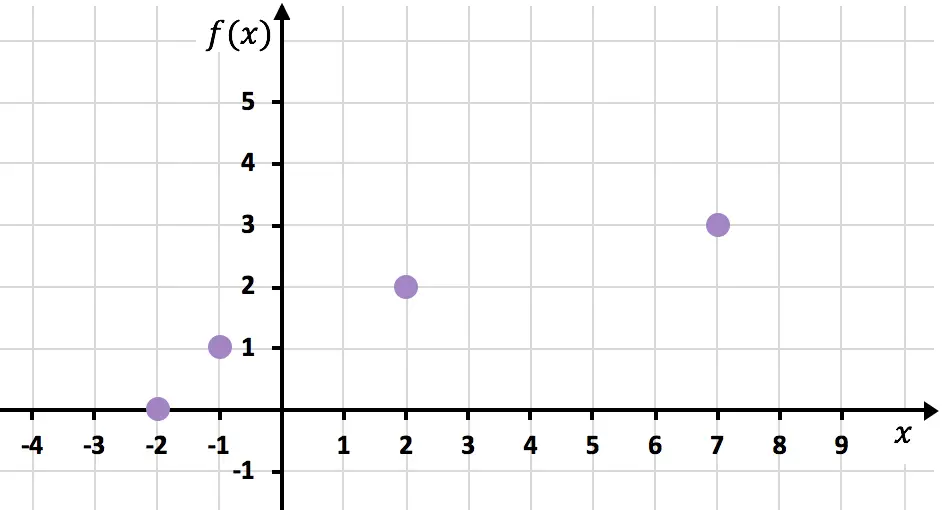
bagaimana merepresentasikan fungsi radikal atau irasional

Dan terakhir, kita gabungkan titik-titiknya dan perpanjang kurvanya untuk menunjukkan bahwa fungsinya terus bertambah:

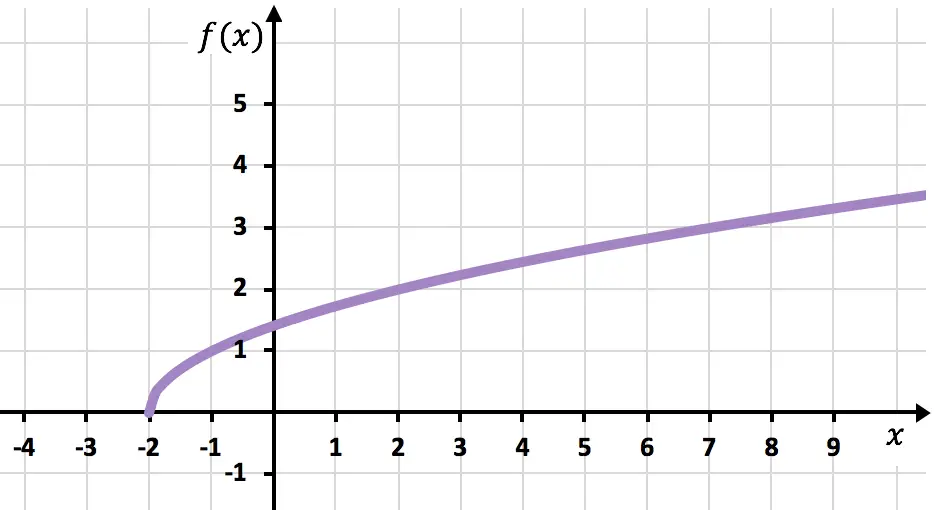
contoh representasi grafis dari fungsi radikal atau irasional

Latihan terpecahkan tentang fungsi irasional atau radikal

Latihan 1

Temukan domain dari fungsi radikal berikut:

$\sqrt{3x+6}$

Lihat solusinya

Akar kuadrat dari bilangan negatif tidak ada. Oleh karena itu, fungsi tersebut akan ada jika argumen akarnya positif atau nol:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Latihan 2

Temukan domain dari fungsi irasional berikut:

$\sqrt{-x+2}$

Lihat solusinya

Akar kuadrat suatu bilangan negatif tidak mempunyai penyelesaian nyata. Oleh karena itu, fungsi tersebut akan tetap ada selama isi akarnya positif atau nol:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

Ingatlah bahwa jika dalam suatu pertidaksamaan kita mengubah sisi suatu bilangan negatif yang dikalikan atau dibagi, kita juga harus memutar tanda pertidaksamaannya tersebut.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Latihan 3

Gambarkan fungsi irasional berikut pada grafik:

$f(x)= \sqrt{x-1}$

Lihat solusinya

Pertama-tama, kita harus menghitung domain dari fungsi tersebut:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Sekarang kita membuat array nilai dengan memberikan nilai fungsi dalam rentang domain:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Terakhir, kita plot titik-titiknya dan plot fungsinya pada grafik:

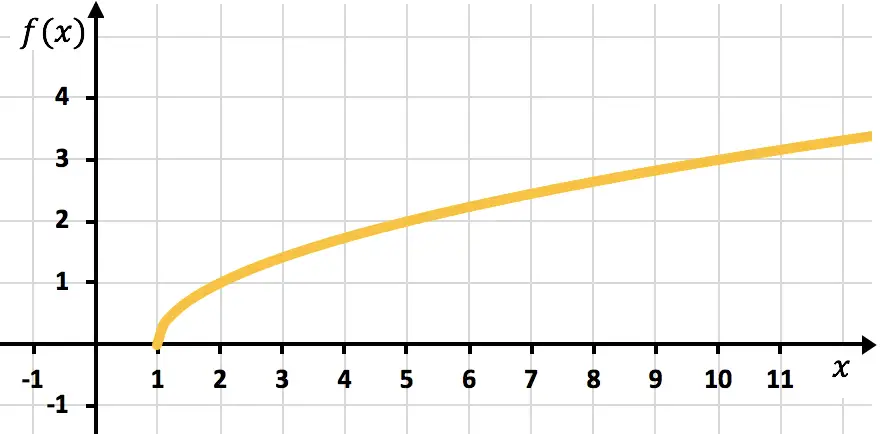
latihan diselesaikan langkah demi langkah dari fungsi irasional atau radikal

Latihan 4

Gambarkan fungsi irasional atau radikal berikut:

$f(x)= -2\sqrt{x}+3$

Lihat solusinya

Pertama-tama, kita harus menghitung domain dari fungsi tersebut:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Sekarang kita membuat array nilai dengan memberikan nilai fungsi dalam rentang domain:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Terakhir, kita plot titik-titiknya dan menggambar fungsinya pada grafik:

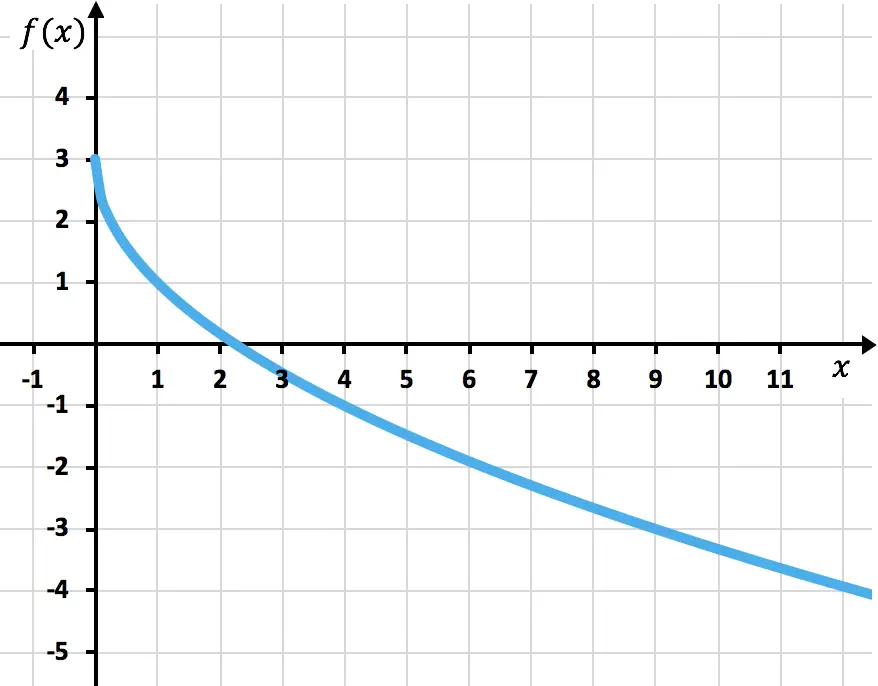
Latihan 5

Gambarkan fungsi irasional atau radikal berikut:

$f(x)= \sqrt{-x+5}$

Lihat solusinya

Sebelum memplot suatu fungsi, kita perlu menghitung domain dari fungsi tersebut:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

Ingatlah bahwa jika dalam suatu pertidaksamaan kita mengubah sisi suatu bilangan negatif hasil perkalian atau pembagian, kita juga harus mengubah tanda pertidaksamaannya.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Sekarang kita membuat tabel nilai dengan mengevaluasi fungsi pada titik-titik yang termasuk dalam domain fungsi:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

Dan terakhir, nyatakan saja titik-titiknya dan cat fungsinya pada grafik:

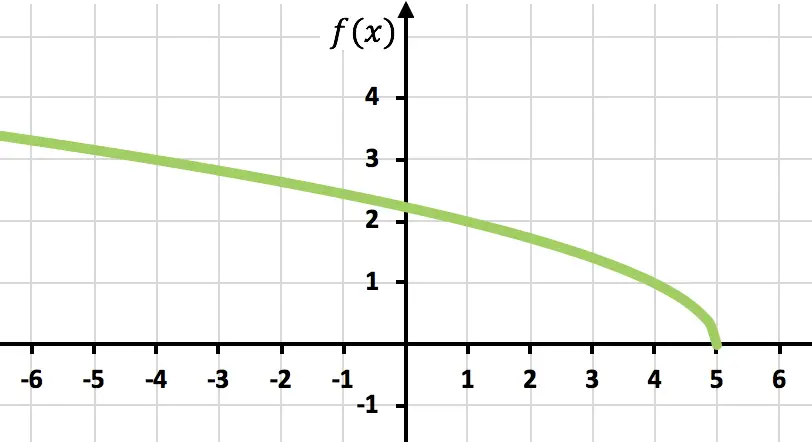
pelaksanaan fungsi radikal atau irasional yang ditentukan

Latihan 6

Gambarkan fungsi irasional atau radikal berikut pada grafik:

$f(x)= \sqrt{x^2-5x+4}$

Lihat solusinya

Pertama-tama kita harus menghitung domain dari fungsi tersebut:

$x^2-5x+4\ge 0$

Dalam hal ini, kita memperoleh pertidaksamaan derajat kedua, jadi kita perlu menerapkan rumus persamaan kuadrat untuk menyelesaikannya:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

Kami membagi garis menjadi tiga bagian dengan akar yang diperoleh:

Dan kami mengganti angka untuk setiap bagian pertidaksamaan, untuk melihat bagian mana yang memenuhi pertidaksamaan tersebut dan, oleh karena itu, termasuk dalam domain:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”> ❌ <p class=$ $x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

✅

Jadi, bagian yang menghormati pertidaksamaan adalah bagian sisinya:

Oleh karena itu, domain fungsinya adalah:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

Setelah kita menghitung domain fungsi, kita membuat tabel nilai yang memberikan nilai fungsi dalam interval domain:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Terakhir, kami merepresentasikan titik-titik yang diperoleh pada grafik dan memplot fungsinya:

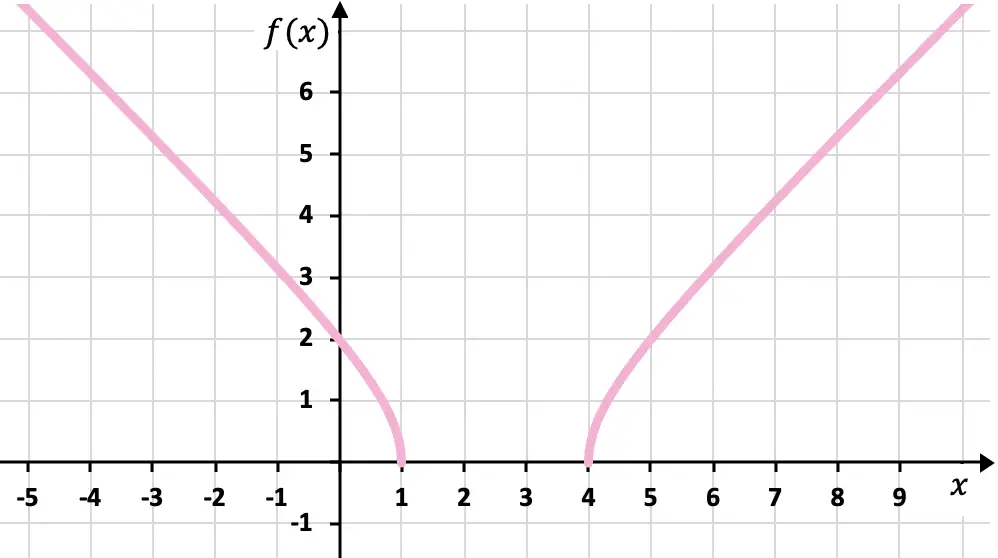
grafik fungsi irasional atau radikal dengan indeks genap

Latihan 7

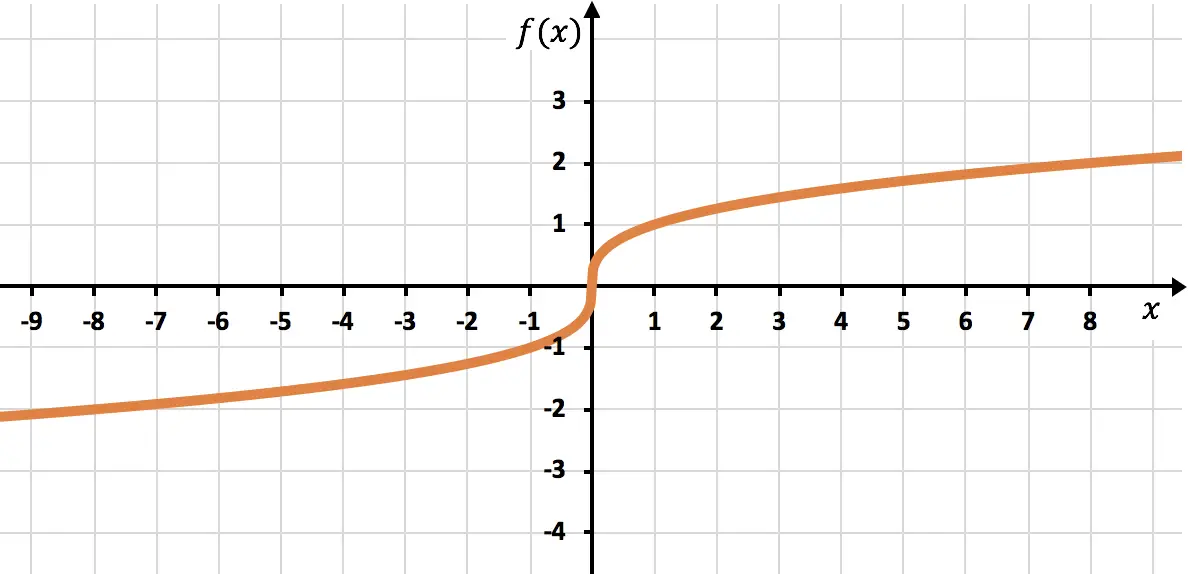
Nyatakan pada grafik fungsi berikut yang dibentuk oleh akar:

$f(x)= \sqrt[3]{x}$

Lihat solusinya

Merupakan fungsi irasional yang akarnya mempunyai indeks ganjil, sehingga domain fungsi tersebut terdiri dari bilangan real:

$\text{Dom } f = \mathbb{R}$

Oleh karena itu, kita dapat mengambil titik mana saja untuk membuat tabel nilai. Dalam hal ini kita akan mencari banyak titik karena merupakan akar pangkat tiga:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Terakhir, kami memplot titik-titik yang ditemukan dan memplot fungsinya pada grafik:

buat grafik fungsi irasional atau radikal dengan indeks ganjil

Latihan 8

Selesaikan soal berikut yang berkaitan dengan fungsi irasional (atau radikal):

Konsumsi baterai ponsel diberikan oleh fungsi berikut:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Dimana konsumsinya dinyatakan dalam miliampere (mA) dan

$t$

adalah waktu yang berlalu dalam hitungan menit.

Tentukan nilai konstanta tersebut

$K$

sehingga setelah 4 menit konsumsinya menjadi 35 mA.

Lihat solusinya

Setelah 4 menit konsumsinya menjadi 35 mA berarti ketika t = 4, f(t) adalah 35. Jadi f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Sekarang kita perlu menyelesaikan persamaan yang kita peroleh. Jika diperhatikan lebih dekat, ini adalah persamaan irasional karena memiliki akar. Dalam persamaan jenis ini, hal pertama yang harus dilakukan adalah mengisolasi akar salah satu ruasnya, yang dalam hal ini sudah terisolasi. Setelah diisolasi, kita harus mengkuadratkan kedua ruas persamaan:

$\left( \sqrt{4-K} \right)^2= 35^2$