▷ Faktorial suatu bilangan: apa itu dan bagaimana cara menghitungnya ✅

Halaman ini menjelaskan apa itu faktorial suatu bilangan dan cara menghitungnya. Selain itu, disajikan beberapa contoh dan tabel nilai faktorial yang paling banyak digunakan. Ini juga mengajarkan cara menghitung faktorial suatu bilangan dengan kalkulator. Dan terakhir, penerapan dan sifat faktorial diilustrasikan.

Berapakah faktorial suatu bilangan?

Dalam matematika, faktorial suatu bilangan sama dengan hasil kali semua bilangan bulat positif dari 1 sampai bilangan tersebut. Selain itu, faktorial suatu bilangan diwakili oleh tanda seru (!) setelah bilangan tersebut.

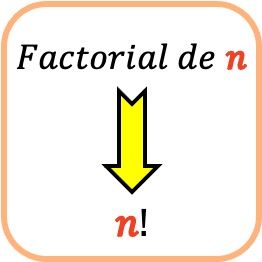
Misalnya, untuk menentukan faktorial suatu bilangan n , disebut juga faktorial n , Anda harus mengalikan bilangan n dengan semua bilangan bulat yang mendahuluinya (dimulai dengan satu):

$n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n$

Cara menghitung faktorial suatu bilangan

Setelah kita melihat arti faktorial suatu bilangan, mari kita lihat dengan contoh cara menentukan faktorial apa pun:

Hitung faktorial dari 4:

Seperti yang kita lihat dalam definisi matematisnya, faktorial suatu bilangan setara dengan perkalian semua bilangan bulat positif yang kurang dari atau sama dengan bilangan tersebut. Oleh karena itu, untuk menghitung faktorial dari 4, kita perlu mengalikan angka 1, 2, 3 dan 4:

$4! = 1 \cdot 2 \cdot 3 \cdot 4 =24$

Faktorial dari 4 menghasilkan 24.

Contoh faktorial bilangan

Untuk menyelesaikan pemahaman tentang pengertian faktorial suatu bilangan, kami berikan kepada Anda contoh menghitung beberapa faktorial dari bilangan yang berbeda:

Faktorial dari 3:

$3! = 1 \cdot 2 \cdot 3 =6$

Faktorial dari 5:

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$

Faktorial dari 6:

$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=720$

Faktorial dari 1:

$1! = 1$

Logikanya, faktorial bilangan 1 sama dengan 1, karena cukup dikalikan 1.

Faktorial dari 0:

$0! = 1$

Ya oke, yang mengejutkan, faktorial dari 0 tidak sama dengan nol, melainkan 1. Ini mungkin tampak sedikit aneh bagi Anda, karena secara teori Anda harus mengalikan 0 dengan 1. Namun, secara konvensi diterima bahwa 0! =1 karena properti produk kosong . Kami meninggalkan tautan ini untuk Anda jika Anda ingin tahu lebih banyak, meskipun tidak terlalu relevan mengetahui alasannya, yang penting Anda ingat bahwa faktorial dari 0 sama dengan 1 .

Daftar hasil faktorial bilangan

Di bawah ini kami telah merangkum faktorial dari bilangan-bilangan yang paling sering digunakan dalam sebuah tabel, sehingga Anda tidak perlu menghitungnya secara manual.

Nomor	Faktorial dari bilangan tersebut
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5.040
8	40.320
9	362.880
sepuluh	3.628.800
sebelas	39.916.800
12	479.001.600
13	6.227.020.800
14	87 178 291 200
limabelas	1.307.674.368.000
16	20.922.789.888.000
17	355.687.428.096.000
18	6.402.373.705.728.000
19	121.645.100.408.832.000
dua puluh	2.432.902.008 176.640.000
lima puluh	3.041.409.320 · ^10,64
100	9.332 621.544 · ^10.157
1.000	4.023.872.601 · ^10.2567
10.000	2.846.259.681 · ^10,35.659
100.000	2 824 229 408 · 10 ^{45 6573}
1.000.000	8.263.931.688 · 10 ^5.565.708

Faktorial suatu bilangan dengan kalkulator

Seperti yang terlihat pada contoh sebelumnya, hasil faktorial dari dua bilangan berurutan bertambah secara eksponensial, sehingga cukup sulit untuk mengetahui faktorial dari bilangan besar. Jadi kami akan menunjukkan cara mencari faktorial suatu bilangan dengan kalkulator.

Kalkulator ilmiah mempunyai kunci dengan simbol x! atau tidak! yang digunakan untuk menghitung faktorial suatu bilangan bulat. Jadi, untuk menentukan nilai faktorial, Anda harus melakukan urutan berikut pada kalkulator:

$n! \quad \color{red} \bm{\longrightarrow} \quad \color{black} n\rightarrow \boxed{x!} \rightarrow \boxed{=}$

Biasanya, kalkulator CASIO memiliki kunci faktorial x! atau tidak! di atas tombol x ^-1 .

Sebagai contoh, kita akan menyelesaikan faktorial dengan kalkulator sehingga Anda dapat memastikan bahwa Anda tahu cara menyelesaikannya. Misalnya, kita akan melakukan faktorial dari 9:

$9! \quad \color{red} \bm{\longrightarrow} \quad \color{black} 9\rightarrow \boxed{x!} \rightarrow \boxed{=} \rightarrow 362880$

Untuk mencari faktorial dari 9 Anda harus memasukkan angka 9 terlebih dahulu, lalu tekan tombol

$\boxed{x!}$

dan terakhir, tekan tombol sama. Dalam hal ini, kalkulator akan menunjukkan kepada kita hasil 362.880.

Penerapan bilangan faktorial

Fungsi faktorial suatu bilangan mungkin tampak seperti operasi yang sangat sederhana dan tidak masuk akal, tetapi dalam aljabar tingkat lanjut fungsi ini cukup sering digunakan. Kita kemudian akan melihat kegunaan utama dari faktorial.

Pertama-tama, faktorial adalah operasi penting untuk menghitung bilangan kombinatorial , lebih dari operasi partikular. Jika Anda belum mengetahui apa itu bilangan kombinatorial, Anda dapat melihat terdiri dari apa dan cara menghitungnya di tautan ini, di mana Anda akan menemukan contoh, latihan yang diselesaikan, dan apa saja propertinya. Selain itu, Anda akan dapat melihat kegunaannya karena memiliki banyak aplikasi di dunia nyata.

Faktorial juga digunakan dalam matematika untuk menentukan polinomial Taylor suatu fungsi.

Demikian pula faktorial digunakan untuk menyelesaikan masalah kombinatorial tertentu, khususnya untuk menghitung kombinasi dan permutasi. Dalam pengertian ini, faktorial juga sering digunakan untuk menghitung probabilitas menggunakan kombinatorik.

Permutasi dari n elemen berhubungan dengan setiap susunan berbeda yang dapat dibuat dengan elemen-elemen tersebut. Jadi, untuk menghitung permutasi digunakan faktorial. Misalnya, jika dalam suatu soal ingin mencari banyaknya kemungkinan susunan 7 benda, maka harus menghitung faktorial dari 7.

Sekarang mari kita lihat latihan yang terselesaikan:

Kita mempunyai 5 pasang sepatu yang berbeda, berapa cara kita menyusunnya?

Dalam latihan ini kita harus menemukan semua cara yang mungkin untuk menggabungkan 5 pasang sepatu ini dengan mempertimbangkan urutan penempatannya. Jadi untuk menyelesaikan soal tersebut Anda hanya perlu menghitung faktorial dari 5:

$5! = 1\cdot 2 \cdot 3\cdot 4\cdot 5 =120$

Singkatnya, 5 pasang sepatu dapat ditempatkan dalam 120 cara berbeda.

Sifat-sifat bilangan faktorial

Bilangan faktorial mempunyai ciri-ciri sebagai berikut:

Karena dua bilangan bulat positif n dan m sedemikian rupa sehingga n lebih besar dari m , maka jelas nilai faktorial n lebih besar dari nilai faktorial m .

$n>m \quad \longrightarrow \quad n! > m!” title=”Rendered by QuickLaTeX.com” height=”15″ width=”183″ style=”vertical-align: -2px;”> <ul style=$

Faktorial suatu bilangan dapat didekomposisi secara faktorial sehingga salah satu faktornya merupakan faktorial dari suatu bilangan yang lebih kecil.

$n>m \quad \longrightarrow \quad n!= n\cdot (n-1) \cdots (m+1)\cdot m!” title=”Rendered by QuickLaTeX.com” height=”19″ width=”361″ style=”vertical-align: -5px;”> Misalnya, 6 lebih besar dari 4, maka persamaan faktorial dari 6 dapat disederhanakan sebagai berikut: <p class=$ $6! = 6 \cdot 5 \cdot 4!$

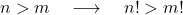
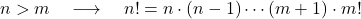
Ekspresi aljabar berikut berlaku untuk faktorial bilangan apa pun, kecuali faktorial 1:

$\displaystyle n!< \left( \frac{n+1}{2} \right)^n$

Faktorial dari bilangan negatif atau desimal

Kita baru saja melihat cara mencari nilai faktorial suatu bilangan bulat positif, tapi… bisakah kita menghitung faktorial suatu bilangan negatif atau bilangan desimal? Jawabannya adalah ya, tetapi diperlukan pengetahuan matematika tingkat lanjut.

Faktorial dari bilangan negatif dan bilangan desimal dihitung menggunakan fungsi khusus yang disebut “Fungsi Gamma” Euler, yang didefinisikan oleh integral berikut:

$\displaystyle \Gamma(z)=\int_0^\infty t^{z-1} e^{-t}\, \mathrm{d}t$

Jadi, semua jenis faktorial dapat diselesaikan dengan fungsi Gamma karena persamaan berikut selalu benar:

$n! = \Gamma(n+1)$

Jadi untuk mencari faktorial 0,5 misalnya kita harus mencari nilai

$\Gamma(1,5)$

Karena:

$0,5! = \Gamma(0,5+1) =\Gamma(1,5)$

Dan solusi integralnya akan sesuai dengan faktorial 0,5.

Tentunya menyelesaikan integral fungsi Gamma tidaklah mudah dan kami tidak akan mengajarkannya pada artikel ini, karena banyak konsep matematika yang harus dijelaskan terlebih dahulu. Namun kami ingin Anda mengetahui bahwa ada kemungkinan menghitung faktorial dari bilangan negatif atau bilangan desimal.

Faktanya, sebagai contoh, kami menghitung beberapa nilai faktorial dan desimal negatif:

$\underline{\bm{n}}$	$\underline{\bm{n!}}$
$\displaystyle \left(\frac{1}{2}\right)!$	$\displaystyle \frac{1}{2}\sqrt{\pi}$
$\displaystyle \left(-\frac{1}{2}\right)!$	$\displaystyle \sqrt{\pi}$
$\displaystyle \left(\frac{3}{2}\right)!$	$\displaystyle \frac{3}{4}\sqrt{\pi}$
$\displaystyle \left(\frac{5}{2}\right)!$	$\displaystyle \frac{15}{8}\sqrt{\pi}$