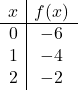Fungsi Nilai Absolut -

Halaman ini menjelaskan apa itu fungsi nilai absolut. Anda juga akan mempelajari cara mendefinisikan fungsi nilai absolut sedikit demi sedikit dan cara merepresentasikan jenis fungsi ini pada grafik. Selain itu, Anda akan melihatnya dengan contoh fungsi nilai absolut dan Anda akan dapat berlatih dengan latihan dan masalah yang diselesaikan langkah demi langkah.

Apa yang dimaksud dengan fungsi bernilai absolut?

Pengertian fungsi nilai mutlak adalah sebagai berikut:

Nilai absolut suatu fungsi mengubah semua citranya menjadi citra positif. Oleh karena itu, jalur fungsi absolut tidak akan pernah bernilai negatif.

Fungsi berikut adalah contoh fungsi nilai absolut:

$f(x)=\lvert 5x \rvert$

Jika ketika mengevaluasi suatu fungsi di suatu titik kita memperoleh hasil positif, maka hasilnya tetap positif:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Sebaliknya jika hasilnya negatif maka menjadi positif:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Fungsi nilai absolut biasanya diberikan di sekolah menengah atas, karena karakteristiknya yang membuat agak sulit untuk dipahami.

Cara mendefinisikan fungsi dengan nilai absolut sedikit demi sedikit

Fungsi bernilai absolut dapat dinyatakan sebagai fungsi sepotong-sepotong. Untuk melakukan ini, Anda harus mengubah tanda fungsi pada interval menjadi negatif.

Mari kita lihat contoh cara beralih dari fungsi nilai absolut ke fungsi sepotong-sepotong:

Nyatakan fungsi berikut dengan nilai absolut sebagai fungsi pemenggalan:

$f(x) = \lvert 4 - x^2 \rvert$

Hal pertama yang perlu kita lakukan adalah menentukan kapan fungsinya negatif. Untuk melakukan ini, kita menetapkan ekspresi aljabar dalam nilai absolut sama dengan 0 dan menyelesaikan persamaan:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Kami sekarang mewakili nilai yang diperoleh pada baris:

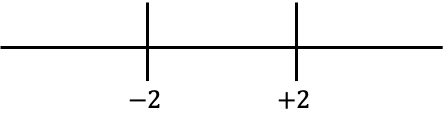
Dan kita lihat tanda mana yang mempunyai fungsi tanpa nilai absolut di setiap interval garis:

$x<-2$

Kita ambil poin apa pun yang kurang dari -2, misalnya

$x=-3:$

$4-(-3)^2$

$-5$

Negatif

$-2 < x < 2$

Kita ambil titik antara -2 dan +2, misalnya

$x=0:$

$4-0^2$

$+4$

Positif

$x>2″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> Misalnya, kita mengambil titik mana pun yang lebih besar dari 2 <p class=$ $x=3:$

$4-3^2$

$-5$

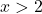
Negatif

Seperti yang telah kita lihat, fungsi tanpa nilai absolut akan bernilai negatif pada intervalnya

$x<-2$

Dan

$x>2.” title=”Rendered by QuickLaTeX.com” height=”14″ width=”47″ style=”vertical-align: -2px;”> Oleh karena itu, kita perlu menyatakan fungsi tersebut dalam tanda hubung dengan mengubah tandanya dalam interval berikut: 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”> 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”> Perhatikan bahwa dalam beberapa interval Anda harus menyertakan kesetaraan. Misalnya disini kita letakkan pada interval kedua <p class=$ $-2 \le x \le 2$

. Namun Anda dapat menempatkannya di interval mana pun yang Anda inginkan selama semua titik kritisnya seimbang. Dengan kata lain, akan sama jika kita mendefinisikan fungsinya sebagai berikut:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Cara merepresentasikan suatu fungsi dengan nilai absolut

Untuk merepresentasikan fungsi dengan nilai absolut pada grafik, kita perlu mengikuti langkah-langkah yang dijelaskan di bawah ini:

Mewakili fungsi seolah-olah tidak memiliki nilai absolut.
Pada interval di mana fungsinya negatif, yaitu terletak di bawah sumbu X, gambarkan fungsi simetrisnya.
Hapus bagian fungsi yang berada di bawah sumbu X.

Mari kita lihat contoh cara membuat grafik suatu fungsi dengan nilai absolut

Gambarkan fungsi berikut dalam nilai absolut:

$f(x) = \lvert -x+2 \rvert$

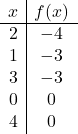
Untuk merepresentasikan suatu fungsi yang mempunyai nilai mutlak, terlebih dahulu kita harus merepresentasikan fungsi yang tidak mempunyai nilai mutlak. Oleh karena itu kami membuat tabel nilai fungsi tanpa nilai absolut:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

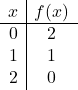
Kami membuat grafik titik-titik dan menggambar garis seolah-olah itu adalah fungsi normal:

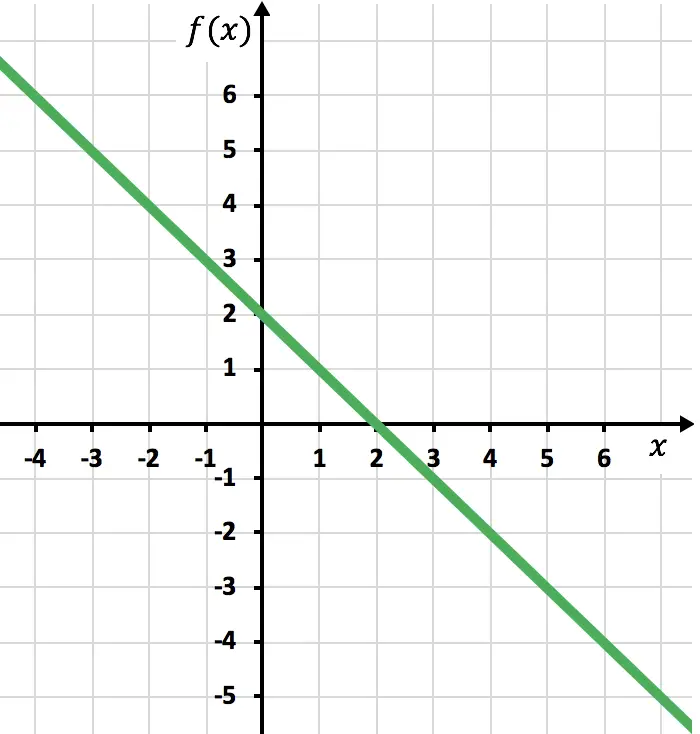
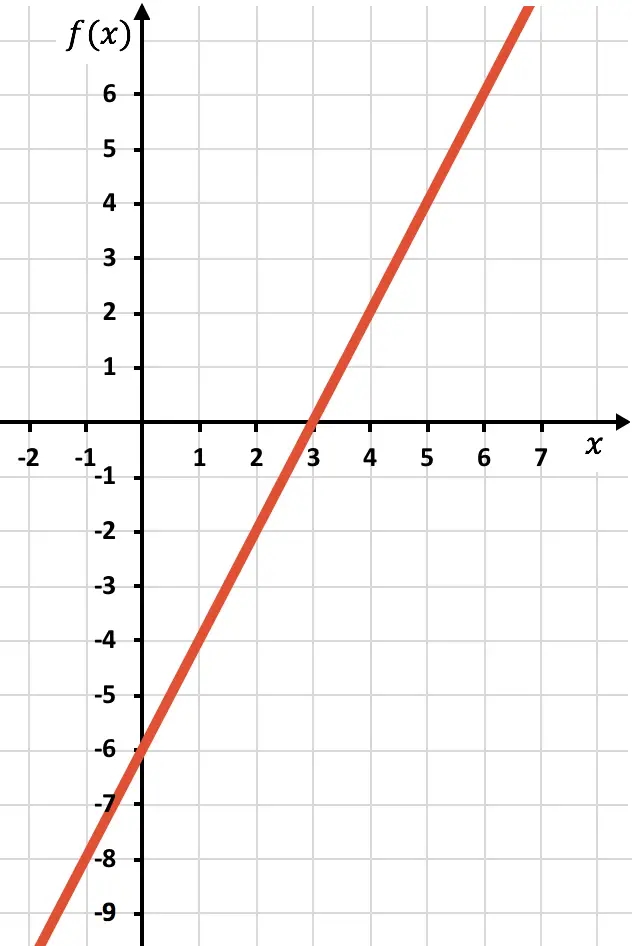
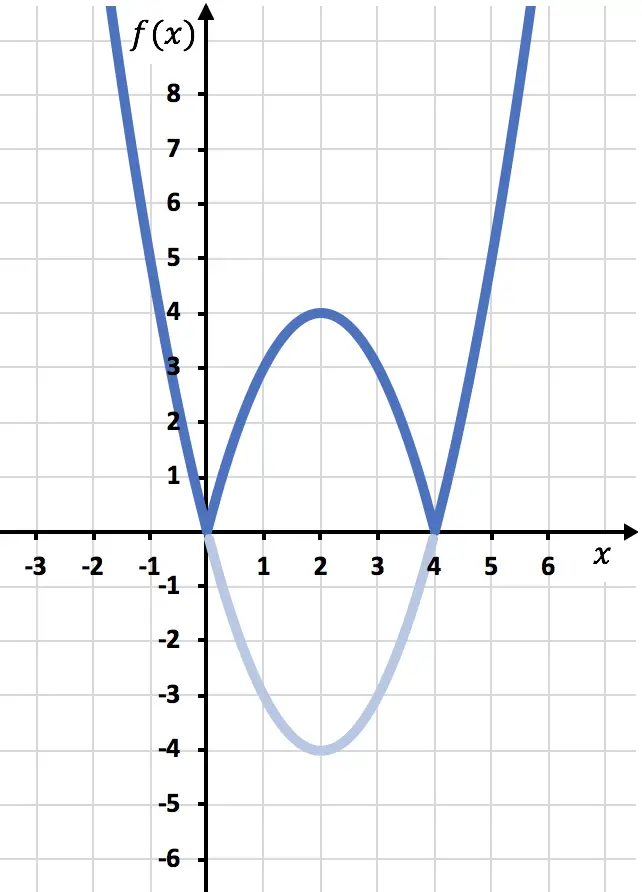
Sekarang kita perlu menggambar fungsi simetris yang fungsinya negatif, yaitu terletak di bawah sumbu x. Oleh karena itu, kita membalik fungsi tersebut mulai dari x=2:

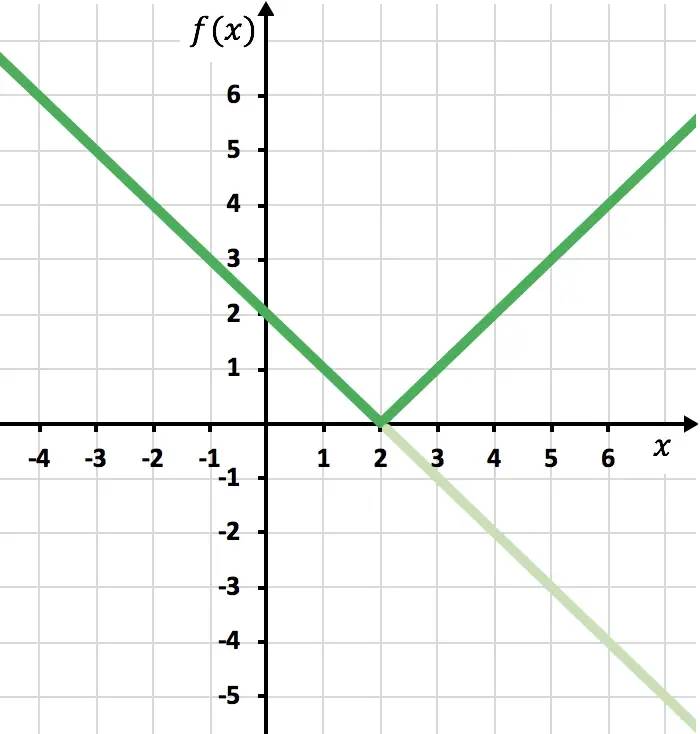
cara merepresentasikan suatu fungsi dengan nilai absolut

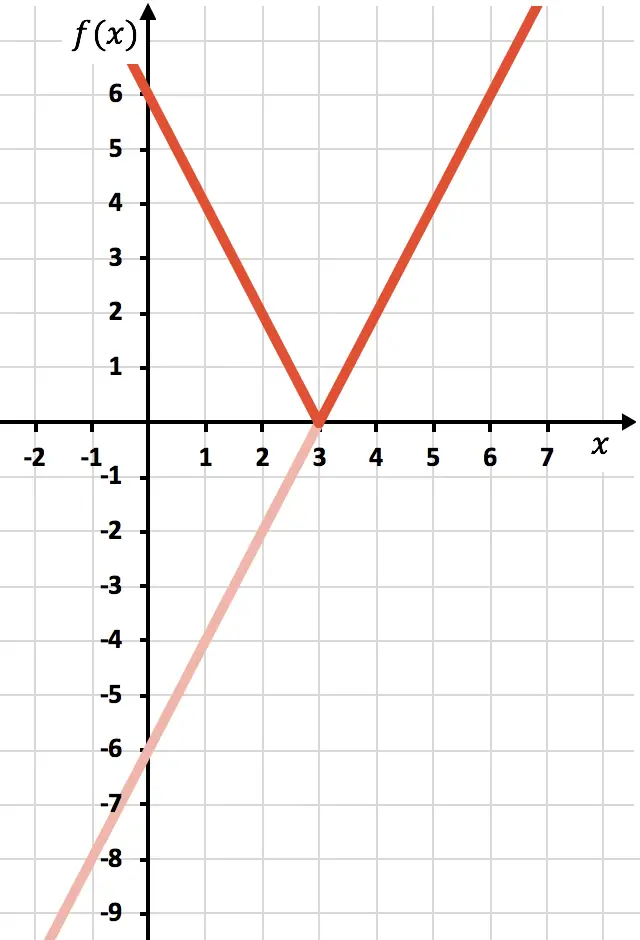
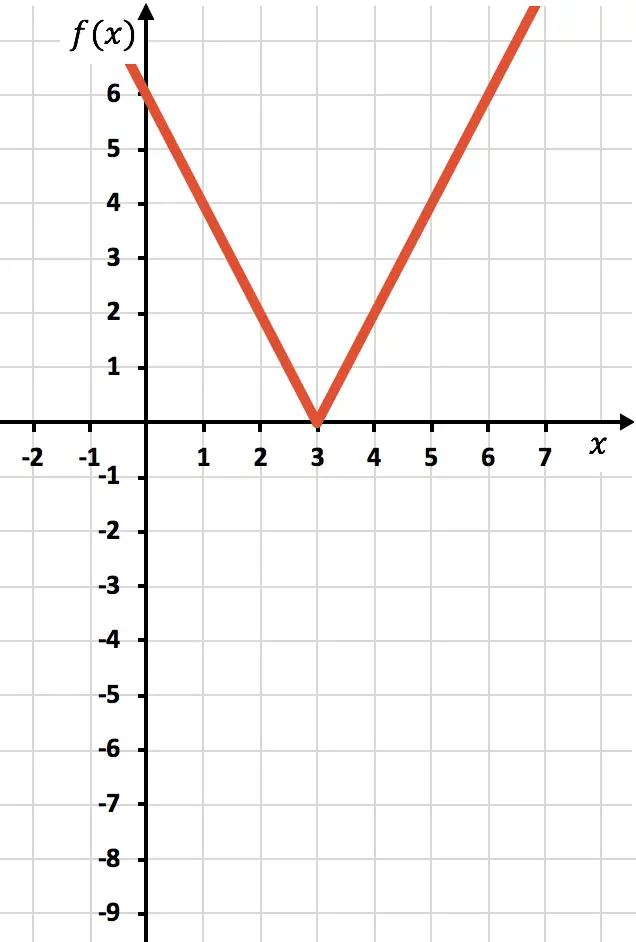
Dan terakhir kita hilangkan jejak fungsi yang terletak di bawah sumbu X:

cara membuat grafik suatu fungsi dengan nilai absolut

Dan dengan cara ini, kita telah merepresentasikan fungsi tersebut dengan nilai absolut. Seperti yang Anda lihat, satu-satunya hal yang berubah adalah kita harus membalikkan bagian fungsi yang terletak di bawah sumbu OX. Oleh karena itu, grafik fungsi apa pun yang bernilai absolut akan selalu terletak pada sisi sumbu semi Y positif.

Sebaliknya, untuk meninjau konsepnya, dari grafik tersebut kita dapat menyimpulkan bahwa domain dari fungsi nilai absolut sebelumnya seluruhnya terdiri dari bilangan real. Sebaliknya, range atau rentang fungsi tersebut dengan nilai absolut hanya terdiri dari bilangan positif dan nol.

Latihan yang diselesaikan pada fungsi nilai absolut

Latihan 1

Nyatakan fungsi berikut dengan nilai absolut sebagai fungsi pemenggalan:

$f(x)= \lvert -x+3 \rvert$

Lihat solusinya

Pertama-tama, kita harus melihat kapan fungsinya negatif. Untuk melakukan ini, kita menetapkan nilai absolut sama dengan nol dan menyelesaikan persamaan:

$-x+3=0$

$x=3$

Kami mewakili nilai yang ditemukan di baris:

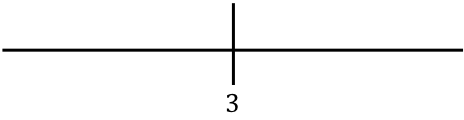
Sekarang kita mengevaluasi sebuah titik di setiap interval fungsi tanpa nilai absolut untuk mengetahui tanda apa yang sebenarnya dimiliki fungsi tersebut di setiap bagian garis:

$x<3$

Misalnya, kita mengambil poin apa pun yang kurang dari 3

$x=0:$

$-0+3$

$+3$

Positif

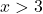$x>3″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ Misalnya, kita mengambil titik mana pun yang lebih besar dari 3

$x=4:$

$-4+3$

$-1$

Negatif

Fungsi tanpa nilai absolut akan menjadi negatif pada interval x>3. Oleh karena itu kita harus menyatakan fungsi tersebut dalam tanda hubung dengan mengubah tandanya dalam interval ini:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Latihan 2

Temukan ekspresi sepotong-sepotong dari fungsi berikut dengan nilai absolut:

$f(x)= \lvert 3x^2-75 \rvert$

Lihat solusinya

Hal pertama yang perlu kita lakukan adalah menentukan kapan fungsinya negatif. Untuk melakukan ini, kita perlu menetapkan argumen nilai absolut sama dengan nol dan menyelesaikan persamaan:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

Sekarang kita nyatakan akar-akar fungsi yang diperoleh di sebelah kanan:

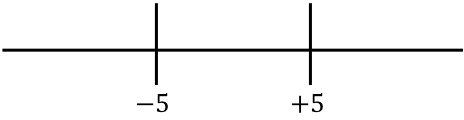
Dan kita lihat tanda mana yang mempunyai fungsi tanpa nilai absolut di setiap interval garis:

$x<-5$

Misalnya, kita mengambil poin apa pun yang kurang dari -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positif

$-5 < x < 5$

Kita ambil titik antara -5 dan +5, misalnya

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Negatif

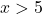$x>5″ title=”Rendered by QuickLaTeX.com” height=”15″ width=”42″ style=”vertical-align: -2px;”> <p class=$ Misalnya, kita mengambil poin apa pun yang lebih besar dari 5

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positif

Oleh karena itu, fungsi tanpa nilai absolut hanya akan bernilai negatif pada interval -5<x<5. Oleh karena itu, kita perlu menyatakan fungsi tersebut dalam beberapa bagian dengan hanya mengubah tanda interval ini:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”> 5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”> <div class=$

Latihan 3

Untuk merepresentasikan suatu fungsi dengan nilai absolut, Anda harus terlebih dahulu merepresentasikan fungsi tanpa nilai absolut:

Ini adalah fungsi affine, jadi Anda perlu membuat tabel nilai untuk mewakilinya secara grafis:

Sekarang kita perlu menggambar fungsi simetris yang fungsinya negatif, yaitu yang terletak di bawah sumbu X. Oleh karena itu, kita membalikkan fungsi dari x=3 ke belakang:

Latihan 4

Untuk merepresentasikan suatu fungsi yang mempunyai nilai mutlak, pertama-tama kita harus menggambar fungsi yang tidak memiliki nilai mutlak.

Ini adalah fungsi kuadrat. Oleh karena itu, untuk merepresentasikannya kita harus menghitung koordinat X titik puncak parabola dengan rumusnya:

Sekarang kita perlu menerjemahkan fungsi tersebut dengan simetri jika nilainya negatif, yaitu di bawah sumbu OX. Oleh karena itu, kita membalikkan fungsi dari x=0 ke x=4: