▷ Teorema sisa: apa itu, contoh dan latihan yang diselesaikan ✅

Di sini Anda akan menemukan penjelasan tentang apa itu teorema sisa (atau teorema sisa) dan bagaimana penerapannya pada polinomial. Anda juga akan dapat melihat contoh dan, sebagai tambahan, berlatih dengan latihan yang diselesaikan langkah demi langkah pada teorema sisanya.

Apa teorema sisanya?

Dalam matematika, teorema sisa mengatakan bahwa sisa pembagian polinomial P(x) dengan polinomial lain berbentuk (xa) sama dengan nilai numerik polinomial P(x) untuk nilai x=a, In dengan kata lain, sisa pembagian P(x):(xa) setara dengan P(a).

Contoh teorema sisa

Setelah kita mengetahui teorema sisanya, mari kita lihat contoh praktis penerapannya:

Hitung sisa pembagian dua polinomial berikut:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Untuk mencari sisa (atau sisa) pembagian polinomial kita dapat memanfaatkan teorema sisa, karena dalam hal ini polinomial pembagi berbentuk (xa), artinya pangkat pertama, koefisien dari variabel x adalah 1 dan mempunyai suku bebas.

Jadi kita menerapkan teorema sisa, yang mengatakan bahwa sisa pembagian seperti ini sama dengan nilai numerik dari polinomial dividen yang dievaluasi dalam suku bebas dari polinomial pembagi yang berubah tanda, yaitu P (1).

Oleh karena itu, untuk mencari sisa pembagian, kita perlu menghitung polinomial di x=1:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

Oleh karena itu, sisa pembagian antar polinomial adalah 2 .

Di sisi lain, kita juga dapat memeriksa dengan aturan Ruffini untuk membagi polinomial bahwa sisanya sama dengan hasil yang kita temukan:

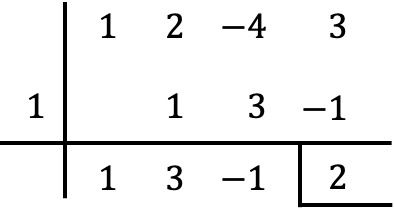
Seperti yang Anda lihat, menentukan sisa pembagian polinomial dengan binomial dengan teorema sisa jauh lebih cepat dan mudah dibandingkan dengan aturan Ruffini, karena lebih sedikit perhitungan yang dilakukan.

Teorema sisa dan faktor

Dari teorema sisa dan definisi akar (atau nol) suatu polinomial kita dapat menyimpulkan teorema faktor. Jadi, teorema faktor menyiratkan hal berikut:

Teorema faktor menyatakan bahwa suatu polinomial P(x) habis dibagi oleh polinomial lain yang berbentuk (xa) jika, dan hanya jika, P(a)=0. Dan, dalam hal ini, berarti a adalah akar atau nol dari polinomial P(x).

Selanjutnya menurut teorema sisa, artinya jika suatu polinomial habis dibagi polinomial lain, maka sisa pembagian tersebut adalah nol, karena P(a)=0.

Misalnya, jika kita mempunyai polinomial tertentu:

$P(x)=x^2+2x-8$

Polinomial ini habis dibagi binomial (x-2) karena P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

Karena x=2 menghilangkan polinomial P(x), ini berarti x=2 adalah akar dari polinomial tersebut.

Dan selanjutnya, karena P(2)=0, kita dapat mengetahui melalui teorema sisa bahwa sisa pembagian

$\cfrac{x^2+2x-8}{x-2}$

sama dengan 0.

Latihan soal teorema sisa

Untuk menyelesaikan pemahaman teorema sisa, kami telah menyiapkan beberapa latihan yang diselesaikan selangkah demi selangkah sehingga Anda dapat berlatih. Kami menyarankan Anda untuk mencoba latihan ini sendiri terlebih dahulu dan kemudian memeriksa apakah Anda melakukannya dengan benar.

Latihan 1

Temukan, berdasarkan teorema sisa, sisa pembagian polinomial

$\cfrac{P(x)}{Q(x)}$

, menjadi polinomial yang terlibat dalam operasi:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Lihat solusinya

Polinomial pembagi hanya terdiri dari suku derajat pertama dan suku bebas, dan terlebih lagi, koefisien suku derajat pertama adalah 1. Oleh karena itu, kita dapat menggunakan teorema sisanya.

Dan untuk menerapkan teorema sisa, cukup dengan mengevaluasi polinomial pembagi pada suku bebas dari tanda perubahan polinomial pembagi, atau dengan kata lain kita harus menghitung P(2).

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

Jadi, sisa pembagian kedua polinomial tersebut adalah 21 .

Latihan 2

Mengingat polinomial

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Temukan sisa yang diperoleh dengan membaginya dengan masing-masing polinomial berikut:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Lihat solusinya

Karena semua polinomial pembagi memenuhi syarat teorema sisa, kita dapat menggunakan teorema ini untuk menentukan sisa setiap pembagian:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Latihan 3

Hitung berapa nilai parameter tersebut

$m$

sehingga sisa pembagian polinomial

$\cfrac{P(x)}{Q(x)}$

sama dengan 3, keduanya polinomial:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Lihat solusinya

Dalam kasus khusus ini, polinomial pembagi terdiri dari monomial derajat pertama dan suku independen dan, terlebih lagi, koefisien monomial derajat pertama adalah 1. Oleh karena itu, kita dapat menggunakan teorema sisanya.

Dan untuk menggunakan teorema sisa, cukup ganti suku bebas dari polinomial pembagi dengan perubahan tanda dimana pada polinomial yang terbagi tersebut terdapat x, oleh karena itu kita harus menyelesaikan P(-3).

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Namun yang jelas kita memperoleh hasil berdasarkan hal yang tidak diketahui

$m.$

Namun, rumusan masalahnya memberitahu kita bahwa sisanya harus sama dengan tiga, jadi kita harus menetapkan sisa yang ditemukan sama dengan 3:

$3m-63 = 3$

Dan akhirnya, kita selesaikan persamaannya:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Latihan 4

Tentukan dengan teorema faktor dan sisa jika polinomial

$P(x)$

habis dibagi polinomialnya

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Lihat solusinya

Sehingga polinomialnya

$P(x)$

habis dibagi polinomialnya

$Q(x)$

pembagian antara kedua polinomial ini harus eksak sehingga sisanya harus nol.

Maka, karena polinomial pembaginya adalah

$(x+2),$

Berdasarkan teorema faktor dan teorema sisa, kita mengetahui bahwa polinomial

$P(x)$

akan habis dibagi polinomialnya

$Q(x)$

jika sudah terisi

$P(-2)=0.$

Oleh karena itu kita harus melihat apakah kesetaraan ini terbukti:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

Memang sisa divisi

$\cfrac{P(x)}{Q(x)}$

sama dengan 0, jadi polinomialnya

$P(x)$

Ya, habis dibagi polinomial lainnya

$Q(x).$

Bagaimana menurut Anda penjelasannya? Apakah kamu menyukainya? Semoga saja demikian! Jangan lupa bahwa Anda dapat meninggalkan saran atau pertanyaan Anda di komentar. ⬇⬇⬇ Kami membacakan semuanya! 😁😁

Teorema sisa (atau residu).

Apa teorema sisanya?

Contoh teorema sisa

Teorema sisa dan faktor

Latihan soal teorema sisa

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Tinggalkan Komentar Batalkan Balasan