Properti penentu

Pada bagian ini, kita akan melihat apa saja sifat-sifat determinan . Kami juga mendemonstrasikan setiap properti dengan sebuah contoh sehingga Anda memahaminya sepenuhnya. Dan, sebagai tambahan, Anda akan menemukan latihan yang berkaitan dengan sifat-sifat determinan.

Di bawah ini kami akan menjelaskan masing-masing sifat determinan satu per satu, namun jika mau, Anda dapat langsung melompat ke tabel ringkasan di bawah ini. 😉

Properti 1: Penentu matriks yang ditransposisikan

Penentu suatu matriks setara dengan determinan matriks yang ditransposisikan.

\lvert A \rvert = \lvert A^t \rvert

Contoh:

\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}

Sekarang kita transposisi matriks 2×2 dan mencari determinannya. Perhatikan bahwa kita memperoleh hasil yang sama seperti sebelumnya:

\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}

Sifat 2: Penentu yang baris atau kolomnya diisi angka nol

Jika suatu determinan memiliki baris atau kolom yang diisi dengan nol, maka determinannya menghasilkan 0.

\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0

Contoh:

\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}

Dalam kedua contoh ini, determinannya bernilai 0. Karena baris kedua dari determinan pertama semuanya nol dan kolom ketiga dari determinan kedua juga semuanya nol.

Sifat 3: Penentu dengan dua baris atau kolom yang sama

Jika suatu determinan mempunyai dua baris atau dua kolom yang sama atau ganda, maka determinannya adalah nol (0).

Oleh karena itu, jika terdapat kombinasi linier antara baris atau kolom, yaitu bergantung linier, maka determinannya menghasilkan 0.

Contoh:

\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0

Dalam hal ini determinannya menghasilkan 0 karena kolom 2 dan 3 sama.

Properti 4: Ubah baris atau kolom determinan

Jika dua baris atau dua kolom dimodifikasi relatif satu sama lain, determinannya memberikan hasil yang sama tetapi dengan tanda yang berbeda.

\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}

Contoh:

\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}

Sekarang kita mengubah urutan kolom 2 dan 3 relatif satu sama lain. Perhatikan bahwa hasilnya sama tetapi dengan tanda yang berbeda:

\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}

Properti 5: Kalikan baris determinan dengan skalar

Mengalikan seluruh elemen pada suatu baris atau kolom dengan bilangan real sama dengan mengalikan hasil determinan dengan bilangan tersebut.

\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

Contoh:

\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}

Sekarang kita ambil determinan yang sama dan mengalikan seluruh garis dengan 2. Anda akan melihat bahwa hasilnya sama dengan determinan sebelumnya tetapi dikalikan dengan 2, atau 10:

\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}

Sifat 6: Penentu hasil kali matriks

Penentu hasil kali dua matriks sama dengan hasil kali determinan masing-masing matriks secara terpisah.

\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert

Contoh:

Untuk mendemonstrasikan sifat determinan ini, kita akan menghitung determinan perkalian dua matriks berikut dengan dua cara yang mungkin:

\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}

Pertama-tama kita kalikan kedua matriks tersebut, lalu kita hitung determinan matriks yang dihasilkan:

\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}

Sekarang kita menghitung determinan masing-masing matriks secara terpisah dan kemudian mengalikan hasilnya:

\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}

Seperti yang Anda lihat, mengerjakan perkalian matriks terlebih dahulu lalu determinannya memberikan hasil yang sama seperti mengerjakan determinan setiap matriks terlebih dahulu lalu mengalikan hasilnya.

Sebaliknya, syarat ini tidak berlaku pada operasi penjumlahan dan pengurangan, artinya determinan penjumlahan (atau pengurangan) dua matriks tidak memberikan hasil yang sama dengan penjumlahan (atau pengurangan) determinan matriks. dua matriks secara terpisah.

Properti 7: Penentu matriks invers

Jika suatu matriks dapat dibalik, maka determinan inversnya sama dengan invers determinan matriks aslinya.

\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}

Contoh:

Kita akan memverifikasi sifat ini dengan terlebih dahulu menghitung invers suatu matriks dan kemudian menyelesaikan determinannya. Kita akan melihat bahwa hasilnya setara dengan mencari determinan matriks asli dan membalikkannya.

Oleh karena itu, kami membalikkan matriks berikut dan menghitung determinannya:

\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}

\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}

\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}

Dan sekarang kita selesaikan determinan matriks asli dan lakukan inversnya:

\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2

\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}

Seperti yang Anda lihat, hasil dari kedua operasi tersebut identik. Oleh karena itu, properti tersebut terbukti.

Properti 8: Gantikan garis penentu

Barisan suatu determinan dapat diganti dengan menjumlahkan (atau mengurangkan) baris yang sama ditambah (atau dikurangi) baris lain dikalikan dengan suatu bilangan.

Contoh:

Dengan contoh berikut kita akan memeriksa properti ini. Kita hitung dulu determinannya, lalu kita operasikan baris determinannya dan hitung ulang hasilnya. Anda akan melihat bagaimana kami memperoleh hasil yang sama dalam kedua kasus.

Jadi, mari kita hitung dulu determinan 3×3 dengan aturan Sarrus:

\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}

Sekarang, pada baris 2, kita tambahkan baris pertama dikalikan 2:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}

Dan kita menyelesaikan determinannya setelah mengubah salah satu garisnya:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}

Dalam kedua kasus tersebut, hasilnya adalah -3. Jadi, terlihat bahwa hasil suatu determinan tidak berubah jika suatu baris diganti dengan jumlah baris yang sama ditambah baris lainnya dikalikan suatu bilangan.

Properti 9: Penentu matriks segitiga

Penentu matriks segitiga adalah hasil kali elemen-elemen diagonal utamanya.

Contoh:

Kita akan menyelesaikan determinan matriks segitiga berikut sebagai contoh:

\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}

Sifat 10: Penentu matriks diagonal

Penentu suatu matriks diagonal sama dengan perkalian elemen-elemen diagonal utamanya.

Contoh:

Mari kita ambil contoh determinan matriks diagonal berikut:

\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}

Tabel ringkasan sifat-sifat determinan

Sifat-sifat determinan yang dijelaskan dapat dirangkum dalam tabel berikut:

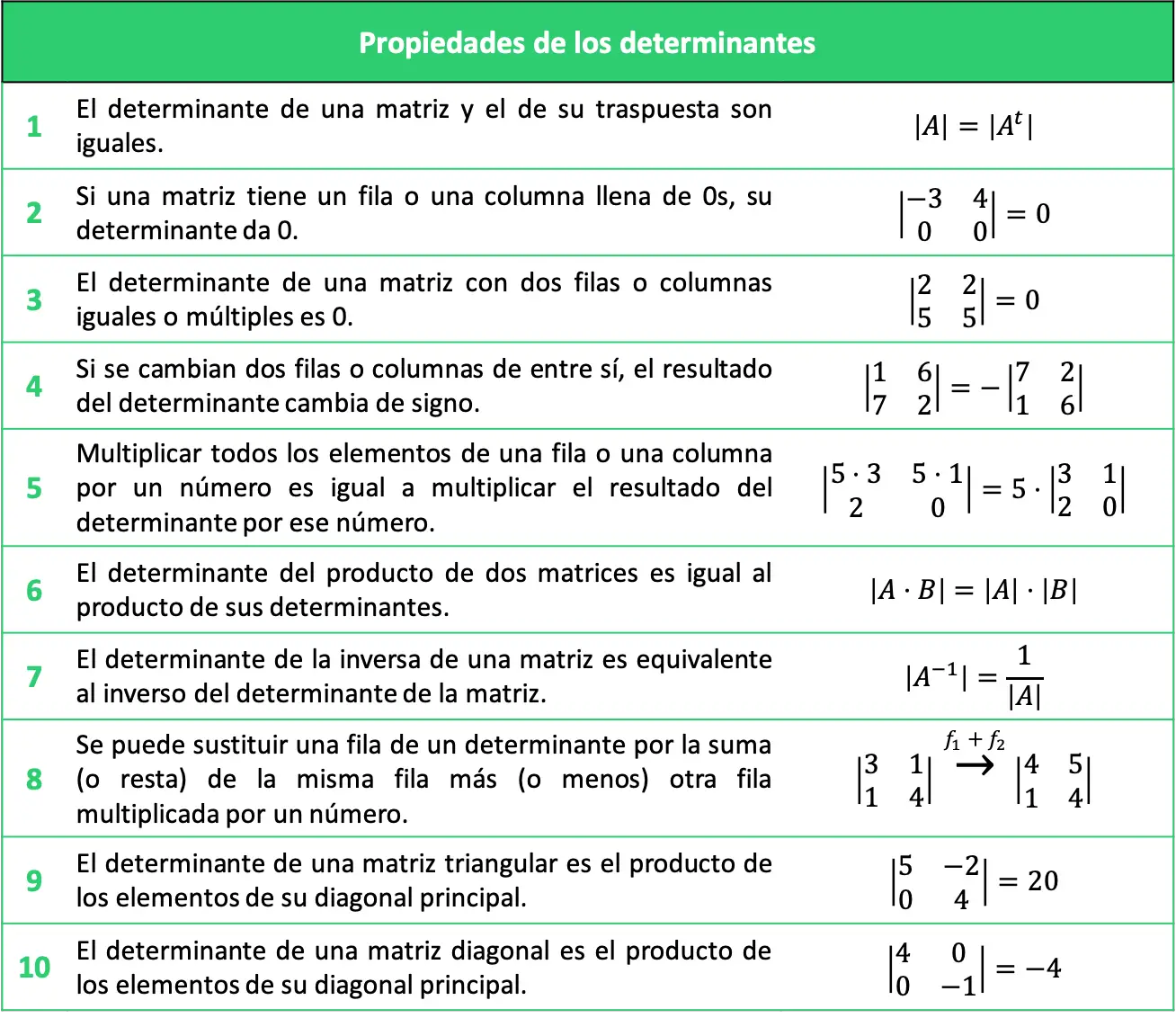
sifat determinan

Latihan soal dengan sifat-sifat determinan

Latihan 1

Selesaikan determinan berikut:

\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}

Jika suatu determinan memiliki baris atau kolom yang diisi dengan nol, determinan tersebut mengembalikan 0 (properti 2). Jadi hasil determinannya adalah 0, karena kolom ketiga diisi angka nol.

Latihan 2

Selesaikan determinan berikut:

\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}

Jika determinan memiliki dua baris atau dua kolom yang sama atau ganda, determinan mengembalikan 0 (properti 3). Jadi hasil determinannya adalah 0, karena baris pertama dan baris ketiga sama.

Latihan 3

Hitung determinan berikut:

\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}

Jika determinan memiliki dua baris atau dua kolom yang sama atau ganda, determinan mengembalikan 0 (properti 3). Jadi hasil determinannya adalah 0, karena kolom keempat adalah dua kali kolom pertama.

Latihan 4

Kita mengetahui hasil suatu determinan, meskipun kita tidak mengetahui elemen-elemen matriksnya:

\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3

Dari hasil determinan sebelumnya dan sifat-sifat determinannya, hitunglah hasil determinan berikut:

\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}

Untuk)

\begin{pmatrix} a & c \\ b & d \end{pmatrix}

adalah matriks yang ditransposisikan dari

\begin{pmatrix} a & b \\ c & d \end{pmatrix}

. Dan determinan suatu matriks sama dengan determinan matriks yang ditransposisikan (properti 1). Jadi, hasil determinannya juga 3.

\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}

b) Dalam menentukan

\begin{vmatrix} b & a \\ d & c \end{vmatrix}

kolom 1 dan 2 telah dimodifikasi sehubungan dengan penentu pernyataan

\begin{vmatrix} a & b \\ c & d \end{vmatrix}

. Oleh karena itu, menurut sifat 4, hasilnya sama dengan hasil penentu pernyataan tersebut tetapi dengan tanda yang berbeda, yaitu -3.

\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}

c) Dalam menentukan

\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}

seluruh kolom kedua determinan pernyataan tersebut telah dikalikan 3. Oleh karena itu, dari sifat 5 dapat disimpulkan bahwa hasilnya juga merupakan hasil determinan pernyataan tersebut dikalikan 3, yaitu 9.

\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}

Latihan 5

Kita mengetahui hasil dari dua determinan ini:

\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8

\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4

Dari informasi tersebut, hitunglah:

\displaystyle \vert A \cdot B \vert

Untuk menghitung hasil determinan tidak perlu mengalikan matriks 4×4. Karena determinan hasil kali dua matriks sama dengan hasil kali determinan masing-masing matriks secara terpisah (sifat 6). Belum:

\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top