Sudut antara garis dan bidang

Di sini Anda akan menemukan cara menghitung sudut antara garis dan bidang. Anda juga akan dapat melihat contoh dan, sebagai tambahan, berlatih dengan latihan yang diselesaikan langkah demi langkah tentang sudut antara garis dan bidang.

Berapakah sudut antara garis dan bidang?

Sudut antara garis dan bidang adalah sudut antara garis dan proyeksi ortogonalnya pada bidang tersebut.

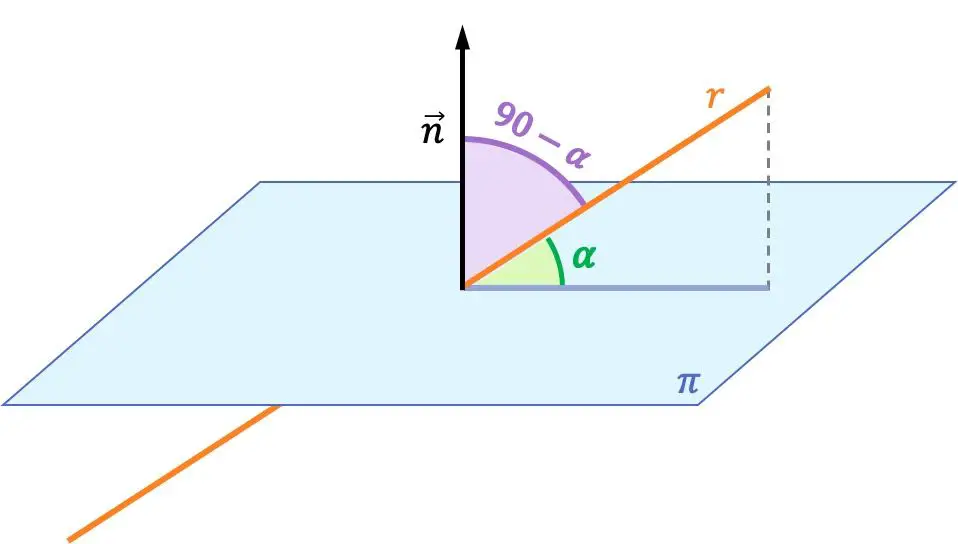
Sudut antara suatu garis dan suatu bidang merupakan komplemen dari sudut antara garis tersebut dengan vektor tegak lurus bidang tersebut. Oleh karena itu, sudut antara garis dan bidang dihitung dari sudut antara vektor arah garis dan vektor normal bidang tersebut.

Rumus sudut antara garis dan bidang

Untuk menyimpulkan rumus sudut antara bidang dan garis, Anda perlu mengetahui cara mencari sudut antara dua vektor . Di halaman tertaut Anda akan menemukan penjelasan serta contoh dan latihan yang diselesaikan langkah demi langkah, jadi jika Anda tidak ingat cara melakukannya, kami sarankan Anda melihatnya.

Jadi, karena sudut antara garis dan bidang berkomplemen dengan sudut antara vektor arah garis tersebut

$(\vv{\text{v}}_r)$

dan vektor normal terhadap bidang tersebut

$(\vv{n})$

, dari rumus sudut antara dua vektor kita menyimpulkan bahwa sudut antara garis dan bidang ekuivalen dengan persamaan berikut:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Jadi, rumus sudut antara garis dan bidang adalah :

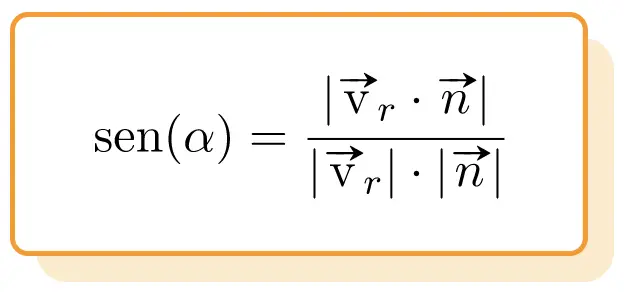
Emas:

$\vv{\text{v}}_r$

adalah vektor langsung dari garis tersebut.
$\vv{n}$

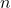
adalah vektor normal terhadap bidang.

Contoh menghitung sudut antara garis dan bidang

Agar Anda dapat mengetahui cara menyelesaikan soal seperti ini, berikut adalah contoh menghitung sudut antara garis dan bidang:

Hitunglah sudut yang dibentuk oleh garis tersebut
$r$

dengan pesawat

$\pi.$

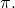
Biarkan persamaannya menjadi:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

Garis tersebut dinyatakan dalam bentuk persamaan parametrik, sehingga vektor arahnya adalah:

$\vv{\text{v}}_r = (-1,4,-3)$

Sebaliknya, bidang didefinisikan dalam bentuk persamaan implisit (atau umum), sehingga vektor normalnya adalah:

$\vv{n} = (1,-1,4)$

Jadi, setelah kita mengetahui vektor arah garis dan vektor normal bidang, kita terapkan rumus sudut antara garis dan bidang:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Kami mengganti vektor dalam rumus:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

Dan kami melakukan perhitungan:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Terakhir, kita membalikkan sinus dengan kalkulator dan mencari nilai sudut:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

Oleh karena itu, sudut antara garis dan bidang kira-kira 51,80º.

Kita harus ingat bahwa jika kita memperoleh hasil 0º, berarti garis dan bidang sejajar atau garis tersebut terdapat di dalam bidang. Dan jika sudutnya sama dengan 90º, berarti garis dan bidang tersebut tegak lurus.

Menyelesaikan masalah sudut antara garis dan bidang

Latihan 1

Temukan sudut yang dibentuk oleh garis

$r$

dengan pesawat

$\pi.$

Biarkan persamaannya menjadi:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

lihat solusi

Garis tersebut dinyatakan sebagai persamaan kontinu, sehingga vektor arahnya adalah:

$\vv{\text{v}}_r = (2,-1,-3)$

Sebaliknya, bidang tersebut berbentuk persamaan implisit (atau umum), sehingga vektor normalnya adalah:

$\vv{n} = (3,1,2)$

Jadi, setelah kita mengetahui vektor arah garis dan vektor normal bidang, kita menggunakan rumus sudut antara garis dan bidang:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Terakhir, kita balikkan sinus dan cari nilai sudutnya:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Jadi, sudut antara garis dan bidang adalah 4,10º.

Latihan 2

Tentukan sudut yang dibentuk oleh garis tersebut

$r$

dengan pesawat

$\pi.$

Biarkan persamaannya menjadi:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

lihat solusi

Garis dinyatakan dengan persamaan implisit (atau umum), oleh karena itu perlu mencari vektor arah garis dengan menghitung hasil kali vektor dari vektor-vektor yang tegak lurus pada 2 bidang yang menentukan garis:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

Sebaliknya, vektor normal bidang adalah:

$\vv{n} = (-4,2,0)$

Jadi, setelah kita mengetahui vektor arah garis dan vektor normal bidang, kita menggunakan rumus sudut antara garis dan bidang:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Terakhir, kita balikkan sinus dan cari nilai sudutnya:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Jadi, sudut antara garis dan bidang adalah 46,33º.

Latihan 3

Tentukan, dengan menggunakan rumus sudut antara garis dan bidang, nilai

$k$

diperlukan untuk hak

$r$

dan pesawat

$\pi$

menjadi paralel.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

lihat solusi

Pertama, garis dinyatakan sebagai persamaan vektor, sehingga vektor arahnya adalah:

$\vv{\text{v}}_r = (4,-1,3)$

Sebaliknya bidang tersebut berbentuk persamaan umum, sehingga vektor normalnya adalah:

$\vv{n} = (4,3,k)$

Jadi, agar dua elemen geometri sejajar, sudut antara keduanya harus nol. Jadi, rumus sudut antara garis dan bidang adalah:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Jadi, perkalian titik antara vektor arah garis dan vektor normal harus sama dengan nol. Dan dari persamaan ini kita dapat menentukan nilai yang tidak diketahui

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Terakhir, jika artikel ini bermanfaat bagi Anda, Anda mungkin juga tertarik dengan cara mencari sudut antara dua bidang . Pada halaman link anda akan menemukan penjelasan yang sangat detail serta rumus yang diperlukan untuk menghitung sudut antara dua bidang yang berbeda dan, sebagai tambahan, anda akan dapat melihat contoh dan latihan yang diselesaikan selangkah demi selangkah untuk dapat berlatih dan memahami. bagaimana hal itu dilakukan dengan sempurna.

Berapakah sudut antara garis dan bidang?

Rumus sudut antara garis dan bidang

Contoh menghitung sudut antara garis dan bidang

Menyelesaikan masalah sudut antara garis dan bidang

Latihan 1

Latihan 2

Latihan 3

Tinggalkan Komentar Batalkan Balasan