▷ Bagaimana saya tahu jika 3 (atau lebih) titik sejajar? ✅

Di halaman ini Anda akan menemukan penjelasan tentang apa itu titik sejajar. Anda juga akan melihat semua metode yang tersedia untuk menentukan apakah 3 (atau lebih) titik sejajar. Terlebih lagi, Anda akan menemukan beberapa contoh dan bahkan latihan yang diselesaikan sehingga Anda dapat berlatih.

Apa maksudnya titik-titik tersebut sejajar?

Dalam geometri analitik, tiga titik atau lebih disejajarkan jika semuanya berada pada garis yang sama, yaitu jika titik-titik tersebut dapat dihubungkan dengan menggambar garis lurus di antara titik-titik tersebut.

Jelasnya, 2 titik akan selalu sejajar, karena Anda selalu dapat menarik garis di antara dua titik. Namun, tiga titik tidak harus berada pada garis yang sama. Pada dasarnya, ada dua metode untuk mengetahui apakah 3 titik atau lebih sejajar:

Metode vektor : terdiri dari melihat apakah vektor-vektor yang membentuk titik-titik sebanding.
Metode persamaan garis : terdiri dari menentukan apakah titik-titik tersebut termasuk dalam garis yang sama.

Di bawah ini adalah penjelasan setiap prosedur dan contohnya sehingga Anda dapat memutuskan mana yang terbaik untuk Anda.

Bagaimana cara mengetahui apakah 3 (atau lebih) titik sejajar dengan metode vektor

Mempertimbangkan tiga poin:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Ketiga titik tersebut sejajar jika vektornya

$\vv{AB}$

Dan

$\vv{BC}$

mempunyai arah yang sama, artinya komponen-komponennya sebanding.

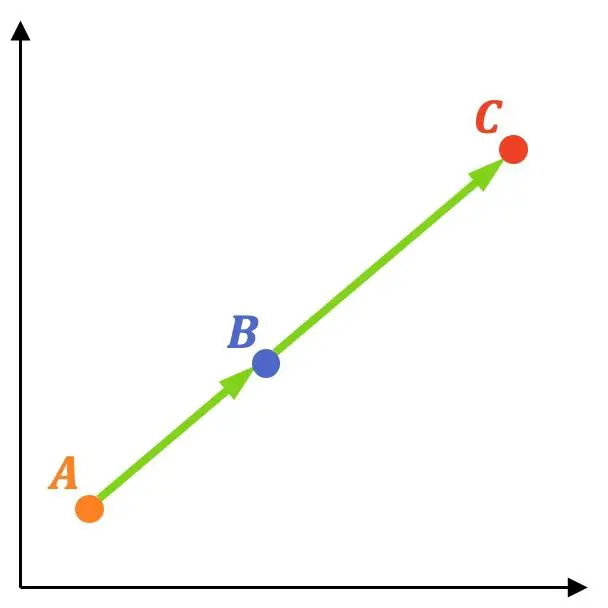
titik-titik yang sejajar pada suatu bidang

Mari kita lihat contoh bagaimana hal ini dilakukan:

Tentukan apakah 3 poin berikut sejajar:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Pertama, kita menghitung vektor antar titik. Cukup menghitung dua vektor berbeda:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

Dan kemudian kita periksa apakah koordinat vektornya proporsional:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

Dengan membagi komponen X dan komponen Y dari kedua vektor tersebut diperoleh hasil yang sama (-2), sehingga vektor-vektor tersebut mempunyai arah yang sama dan oleh karena itu titik-titiknya sejajar .

Cara ini juga dapat digunakan untuk mengetahui apakah tiga titik atau lebih sejajar dalam ruang (pada R3), yang perlu ditambah hanyalah memeriksa apakah komponen ketiga dari kedua vektor tersebut (komponen Z) juga proporsional.

Jika artikel ini bermanfaat bagi Anda, Anda mungkin juga tertarik untuk mengetahui cara menghitung titik tengah antara dua titik , karena tentunya mencari titik tengah 2 titik adalah cara menentukan titik ketiga yang sejajar dengan dua titik lainnya. Anda dapat melihat cara melakukannya di halaman tertaut, selain itu Anda juga dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Cara mengetahui 3 titik (atau lebih) sejajar dengan metode persamaan garis lurus

Seperti yang baru saja kita lihat di bagian sebelumnya, salah satu cara mempelajari keselarasan 3 titik atau lebih adalah dengan menggunakan vektor-vektor yang dapat terbentuk di antara titik-titik tersebut. Nah, cara lainnya adalah memulai dengan persamaan garis:

Mempertimbangkan tiga poin:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Ketiga titik tersebut sejajar jika semuanya berada pada garis yang sama. Oleh karena itu, untuk mengetahui apakah tiga titik atau lebih sejajar, langkah-langkah berikut harus diikuti:

Tentukan persamaan garis yang melalui dua dari tiga titik.
Periksa apakah titik ketiga juga termasuk dalam garis tersebut. Dalam hal ini berarti 3 titik tersebut sejajar, namun jika syarat tersebut tidak terpenuhi berarti titik-titik tersebut tidak sejajar.

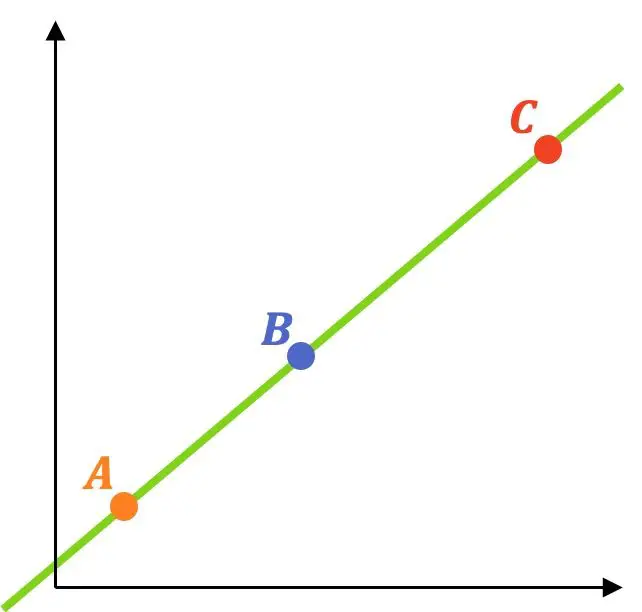
Sebagai contoh, kita akan menyelesaikan latihan menggunakan metode ini:

Periksa apakah 3 poin berikut selaras:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Pertama-tama kita harus menghitung persamaan garis yang melalui titik A dan B. Oleh karena itu, kita mencari vektor arah garis tersebut:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Sekarang Anda harus membuat persamaan garis, Anda dapat memilih jenis yang Anda inginkan: parametrik, implisit, umum, dll. Namun dalam hal ini kita akan menggunakan persamaan kontinu. Jadi persamaan garis kontinu yang melalui titik A dan titik B adalah:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Setelah kita mendapatkan persamaan garisnya, kita harus memeriksa apakah titik lainnya juga termasuk dalam garis yang sama. Caranya, kita substitusikan koordinat titik C ke dalam persamaan garis:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

Kita mendapat hasil seri, jadi titiknya memenuhi persamaan garis. Oleh karena itu, ketiga titik tersebut segaris .

Perlu diperhatikan bahwa himpunan titik-titik yang sejajar tidak harus berjarak sama, artinya jarak antara beberapa titik yang sejajar bisa saja berbeda. Perbedaan kedua konsep tersebut dapat Anda lihat pada penjelasan jarak antara dua titik (geometri) , di mana Anda juga dapat melihat contoh dan latihan yang diselesaikan langkah demi langkah.

Menyelesaikan latihan titik-titik sejajar

Latihan 1

Tentukan apakah 3 poin berikut sejajar:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Lihat solusinya

Kita dapat memilih salah satu dari dua metode yang telah kita lihat untuk memecahkan masalah tersebut. Dalam hal ini kita akan menggunakan metode vektor.

Pertama, kita menghitung vektor antar titik:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

Dan sekarang kita periksa apakah koordinat Cartesian dari vektor-vektor tersebut sebanding:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

Dengan membagi komponen X dan komponen Y kedua vektor satu sama lain diperoleh hasil yang sama (-4), sehingga arah vektor-vektor tersebut sama. Fakta yang menunjukkan bahwa titik-titik tersebut sejajar .