Poin coplanar (atau coplanar)

Di halaman ini Anda akan mengetahui apa itu titik-titik sebidang (atau sebidang) dan bagaimana mengetahui apakah titik-titik tertentu sebidang atau tidak. Selain itu, Anda akan dapat melihat contoh dan latihan dengan latihan poin koplanar yang diselesaikan.

Apa yang dimaksud dengan titik koplanar?

Dalam geometri analitik, arti titik sebidang (atau coplanar) adalah sebagai berikut:

Titik sebidang adalah titik-titik yang berada pada bidang yang sama.

Oleh karena itu, 2 atau 3 titik selalu sebidang karena sebuah bidang dapat dibentuk dengan sedikitnya 3 titik. Sebaliknya, jika terdapat 4, 5 titik atau lebih, ada kemungkinan beberapa titik tersebut tidak berada pada bidang yang sama sehingga tidak sebidang.

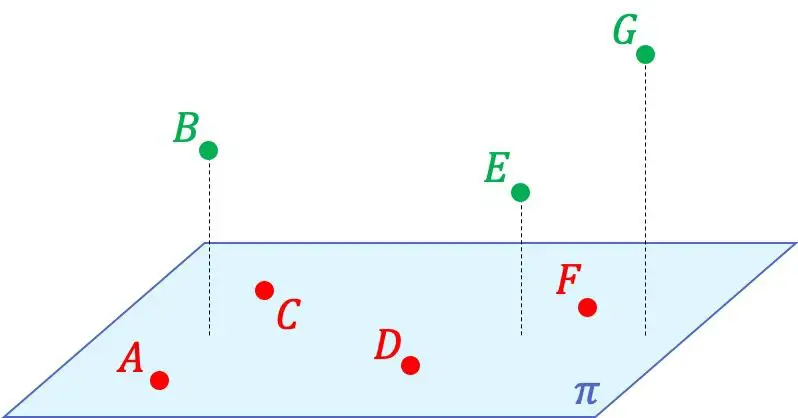
Misalnya, pada representasi grafis di atas, Anda dapat melihat bahwa titik A, C, D, dan F saling sebidang karena terletak pada bidang yang sama. Sebaliknya keempat titik tersebut tidak sebidang dengan titik B, E, dan G, karena tidak ada bidang yang dapat terbentuk pada ruang yang memuat semua titik tersebut.

Dari sifat ini kita dapat menyimpulkan bahwa vektor-vektor yang didefinisikan oleh titik-titik koplanar juga merupakan vektor-vektor koplanar, yaitu terletak pada bidang yang sama.

Kapan titik-titiknya sebidang?

Seperti yang kita lihat dalam definisi titik-titik sebidang (atau sebidang), dua atau tiga titik selalu sebidang, tetapi lebih dari tiga titik tidak harus menghormati hubungan koplanaritas.

Jadi, ada 2 metode utama untuk menentukan apakah empat titik atau lebih adalah koplanar:

Salah satu cara untuk mengetahui apakah titik-titik tersebut sebidang adalah dengan vektor-vektor yang ditentukan oleh titik-titik tersebut: jika vektor-vektor tersebut sebidang , maka titik-titik tersebut juga sebidang.

Tentunya, untuk menerapkan metode ini Anda perlu mengetahui kapan vektor-vektor tersebut koplanar. Namun karena ada juga beberapa cara untuk menentukan apakah suatu himpunan vektor bersifat koplanar, kami sarankan untuk mempelajari cara mengetahui apakah suatu vektor bersifat koplanar . Di sini Anda akan menemukan semua prosedur yang ada untuk mencari 2, 3, 4 atau lebih vektor koplanar, serta contoh dan latihan penyelesaiannya.

Cara lain untuk mengetahui apakah suatu himpunan titik-titik adalah koplanar adalah dengan mencari persamaan bidang yang dibentuk oleh 3 titik dalam himpunan tersebut, dan jika titik-titik lainnya memenuhi persamaan tersebut, berarti semua titik dalam himpunan tersebut adalah koplanar.

Meskipun bergantung pada masalahnya, sebaiknya gunakan metode pertama dari kedua metode tersebut, karena lebih mudah dan cepat untuk memeriksa apakah vektor-vektor tersebut koplanar daripada menghitung persamaan bidang. Tapi, yang jelas, gunakan mana saja yang Anda suka.

Memecahkan masalah titik koplanar

Latihan 1

Tentukan apakah ketiga titik berikut ini sebidang:

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

lihat solusi

Dalam hal ini tidak perlu melakukan perhitungan apapun karena 3 titik selalu sebidang , apapun itu.

Latihan 2

Tentukan apakah keempat titik berikut ini sebidang:

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

lihat solusi

Agar keempat titik tersebut koplanar, vektor-vektor yang ditentukan oleh titik-titik tersebut harus koplanar. Oleh karena itu kami menghitung vektor-vektor ini:

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

Sekarang mari kita buat matriks yang dibentuk oleh vektor-vektor:

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

Agar vektor-vektor yang dihasilkan bersifat koplanar, pangkat matriks sebelumnya harus sama dengan 2. Dan untuk ini, determinan seluruh matriks 3×3 harus sama dengan nol:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

Akan tetapi determinan seluruh matriks bukan nol, sehingga pangkat matriks tersebut adalah 3, sehingga keempat titik tersebut tidak sebidang .

Latihan 3

Cari tahu apakah lima poin berikut ini koplanar:

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

lihat solusi

Agar kelima titik tersebut koplanar, vektor-vektor yang didefinisikan oleh titik-titik tersebut harus koplanar. Oleh karena itu kami menghitung vektor-vektor ini:

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

Sekarang mari kita buat matriks yang terdiri dari vektor-vektor:

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

Agar vektor-vektor yang dihasilkan bersifat koplanar, pangkat matriks sebelumnya harus sama dengan 2. Oleh karena itu, kita menghitung pangkat matriks vektor-vektor dengan determinan untuk memeriksa apakah vektor-vektor tersebut koplanar:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0$

$rg(A)=2$

Pangkat matriksnya setara dengan 2, sehingga vektor-vektornya koplanar dan oleh karena itu 5 titiknya juga koplanar.

Latihan 4

Hitung nilai parameter

$k$

sehingga 4 poin berikut ini koplanar:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

lihat solusi

Agar keempat titik tersebut koplanar, vektor-vektor yang ditentukan oleh titik-titik tersebut harus koplanar. Oleh karena itu kami menghitung vektor-vektor ini:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

Yang matriks vektornya adalah:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Agar vektor-vektor yang dihasilkan bersifat koplanar, pangkat matriksnya harus 2. Oleh karena itu, determinan seluruh matriks 3×3 harus 0:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$

$\displaystyle 2k-3 =0$

Akhirnya, kami menyelesaikan hal yang tidak diketahui

$k:$

$2k =3$

$\bm{k =}\mathbf{\cfrac{3}{2}}$

Terakhir, jika artikel ini bermanfaat bagi Anda, Anda mungkin juga tertarik dengan cara menghitung jarak antara dua titik (rumus) , karena terkadang dalam soal geometri analitik kita ditanyai berapa jarak antara dua titik. Di halaman tertaut Anda akan menemukan penjelasan yang sangat rinci, serta contoh dan latihan yang diselesaikan langkah demi langkah.

Poin koplanar (atau koplanar).

Apa yang dimaksud dengan titik koplanar?

Kapan titik-titiknya sebidang?

Memecahkan masalah titik koplanar

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Tinggalkan Komentar Batalkan Balasan