Di sini Anda akan menemukan segala sesuatu tentang hiperbola: apa itu hiperbola, apa saja unsur-unsur karakteristiknya, bagaimana menemukan persamaannya, contoh, latihan penyelesaiannya, dll.
Apa itu hiperbola?
Hiperbola adalah kurva terbuka dengan dua cabang yang definisi matematisnya adalah sebagai berikut:
Dalam geometri analitik, hiperbola adalah tempat kedudukan titik-titik pada bidang yang memenuhi syarat berikut: nilai mutlak selisih jarak antara setiap titik hiperbola dan dua titik tetap (disebut fokus) harus konstan.
Selanjutnya, nilai pengurangan kedua jarak tersebut selalu setara dengan jarak antara dua titik sudut hiperbola.
![]()

Di bawah ini kita akan melihat apa yang dimaksud dengan koefisien
![]()
dari sebuah hiperbola.
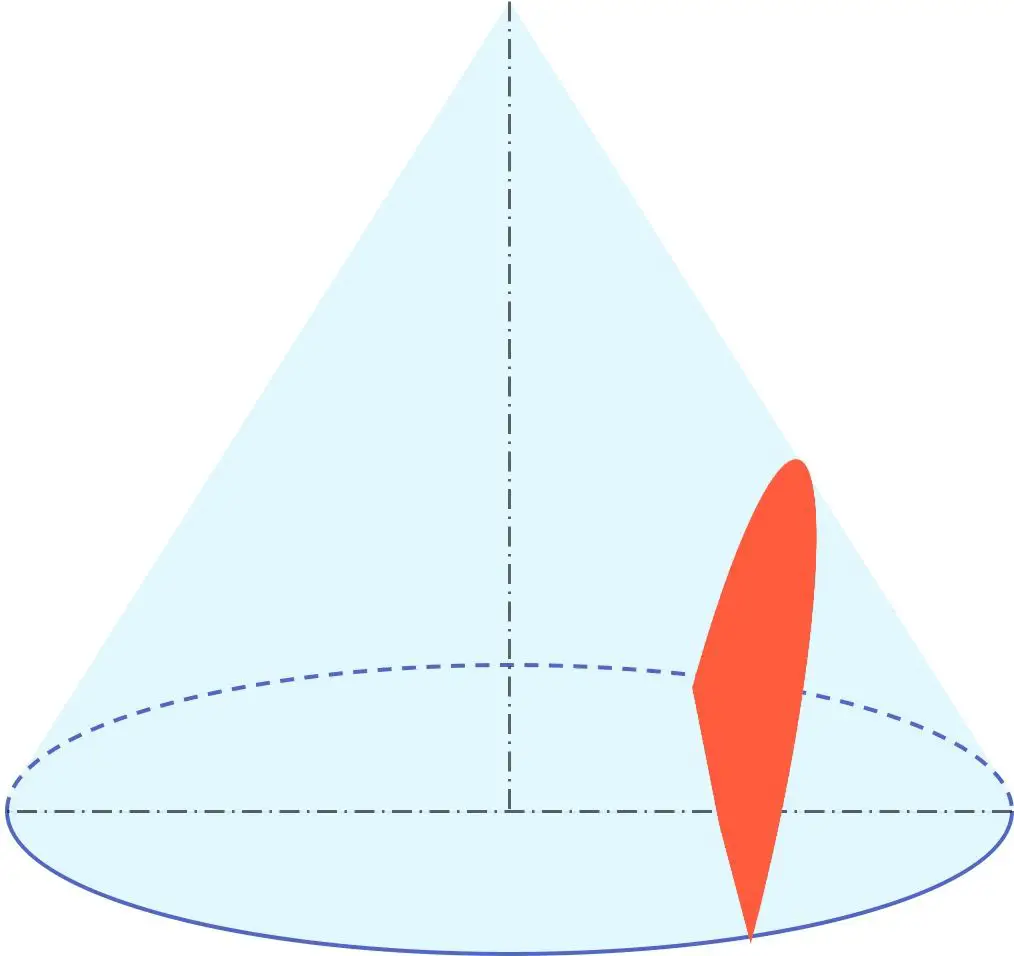
Selain itu, hiperbola merupakan bagian dari kelompok geometri yang disebut kerucut beserta keliling, elips, dan parabola. Oleh karena itu, hiperbola merupakan bagian berbentuk kerucut, atau dengan kata lain dapat diperoleh dari kerucut.
Secara khusus, hiperbola adalah hasil potongan kerucut oleh bidang yang sudutnya lebih kecil dari sudut yang dibentuk oleh generator kerucut terhadap sumbu revolusinya.
Elemen hiperbola
Ciri-ciri hiperbola bergantung pada hal-hal berikut:
- Fokus : ini adalah dua titik tetap yang menjadi ciri setiap hiperbola (titik F dan F’ pada grafik di bawah). Nilai absolut selisih jarak dari setiap titik hiperbola ke setiap fokus adalah konstan dan sama dengan

- Sumbu fokus atau utama : garis yang melalui dua titik fokus hiperbola. Ini sesuai dengan sumbu simetri bangun geometris tersebut. Disebut juga sumbu melintang atau melintang.
- Sumbu sekunder : merupakan garis bagi ruas FF’ (garis yang melalui titik B dan B’). Selain itu, ini adalah garis yang tegak lurus terhadap sumbu fokus dan merupakan sumbu simetri hiperbola lainnya
- Pusat (O) : adalah titik potong dua sumbu dan titik tengah dua titik serta dua titik fokus. Karena hiperbola mempunyai dua sumbu simetri, maka hiperbola juga merupakan pusat simetri.
- Titik sudut (A dan A’) : adalah titik potong cabang-cabang hiperbola dengan sumbu fokus.
- Sinar vektor (R) : ini adalah segmen yang bergerak dari titik mana pun pada hiperbola ke setiap fokus.
- Panjang fokus : ini adalah panjang segmen gabungan antara dua fokus.
- Sumbu utama atau sumbu nyata: merupakan ruas yang bergerak dari titik A ke titik A’, panjangnya setara dengan

- Sumbu kecil atau sumbu imajiner: merupakan ruas yang bergerak dari titik B ke titik B’, panjangnya setara dengan
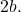
- Asimtot : adalah garis putus-putus yang ditunjukkan pada grafik. Kita akan melihat di bawah bagaimana cara menghitungnya.
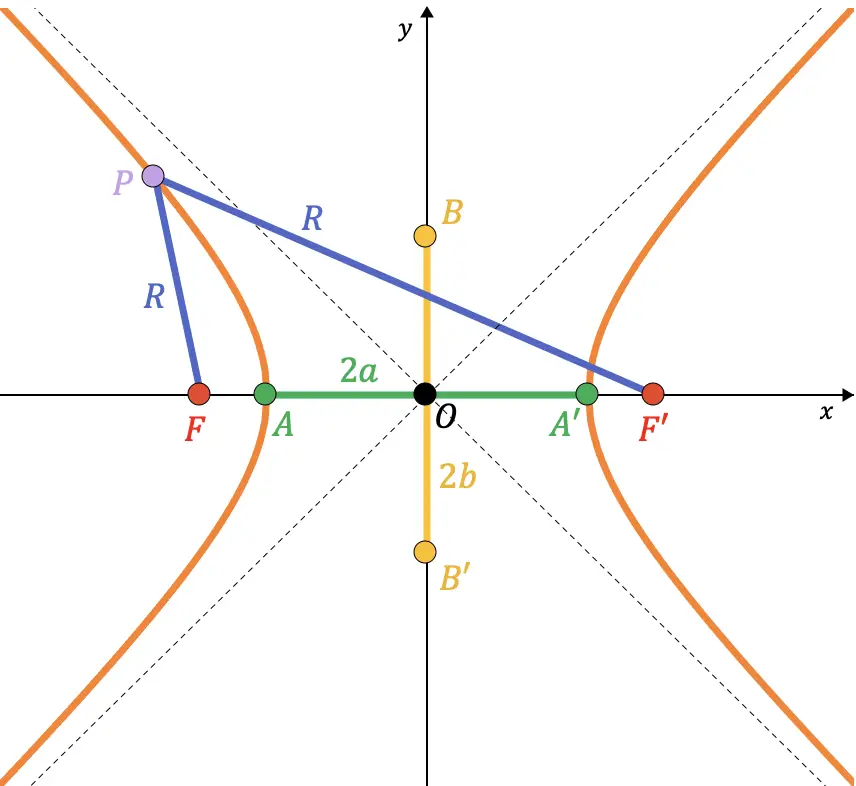
Hubungan antar unsur hiperbola
Pertama-tama, kita katakan bahwa semi-sumbu berarti setengah dari suatu sumbu. Misalnya, semi-sumbu sebenarnya adalah ruas garis dari titik A ke pusat hiperbola, yang panjangnya adalah
![]()
Jadi, terdapat hubungan yang sangat penting antara setengah sumbu nyata, setengah sumbu imajiner, dan setengah panjang fokus. Faktanya, rumus yang akan kita simpulkan selanjutnya banyak digunakan untuk menyelesaikan latihan dan soal hiperbola.
Perlu Anda ketahui bahwa titik B dan B’ pada hiperbola sama dengan titik potong sumbu utama dan jari-jari lingkaran imajiner.
![]()
(jarak semi fokus) dari pusat ke titik A. Oleh karena itu, seperti terlihat pada gambar grafik berikut, ruas yang menghubungkan titik A dan titik B berimpit dengan jari-jari lingkaran tersebut (
![]()
):
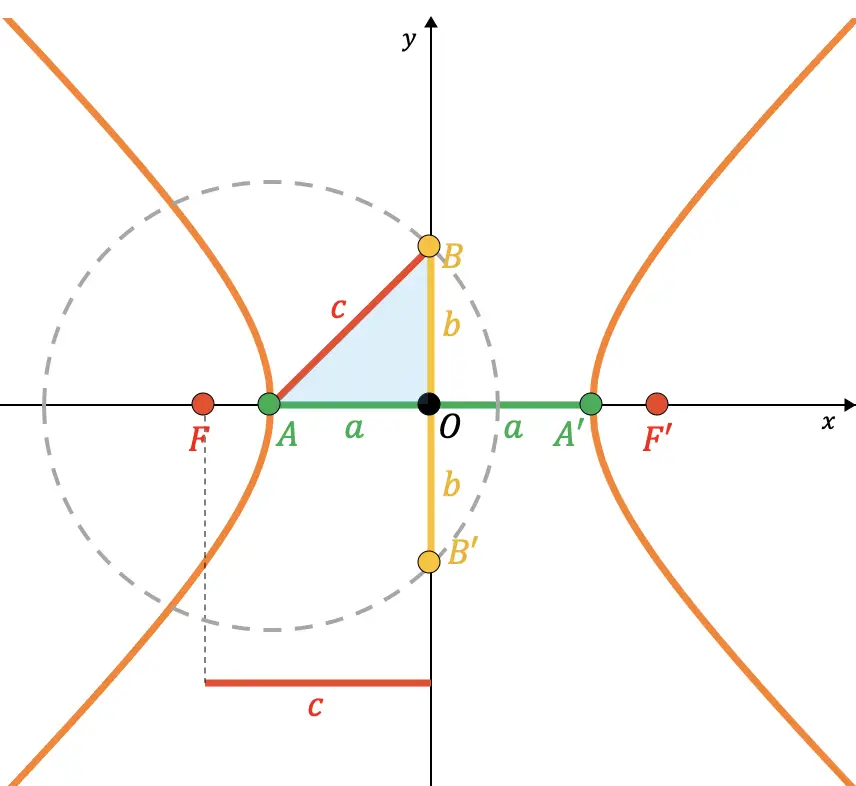
Jadi dapat ditunjukkan dari teorema Pythagoras bahwa ada hubungan antar parameter
![]()
Dan
![]()
adalah sebagai berikut:
![]()
persamaan hiperbola
Ada beberapa jenis persamaan hiperbola, karena bergantung pada sifat-sifatnya, salah satu persamaan tersebut digunakan untuk menyatakannya secara matematis. Selanjutnya, kami akan menganalisis masing-masing secara detail.
Pertama, kita mempunyai persamaan biasa hiperbola. Kedua, kita akan melihat varian persamaan biasa, yaitu persamaan hiperbola tereduksi atau kanonik . Selanjutnya kita akan mempelajari bagaimana persamaan umum hiperbola. Dan terakhir, kita akan menganalisis persamaan dua kasus khusus hiperbola: hiperbola sama sisi dan hiperbola konjugasi .
Persamaan biasa hiperbola
Ketika kita ingin mendefinisikan hiperbola dengan persamaan yang pusat luarnya berada di titik asal (titik (0,0)), kita harus menggunakan rumus berikut:
Rumus persamaan biasa hiperbola koordinat kartesius adalah sebagai berikut:
![]()
Emas:
-

Dan

adalah koordinat pusat hiperbola:
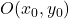
-

adalah panjang sumbu semi-mayor hiperbola.
-

adalah panjang sumbu semi minor hiperbola.
Dengan persamaan ini Anda dapat mendeskripsikan hiperbola yang sumbu fokusnya horizontal (cabangnya terbuka ke kiri dan kanan), yang merupakan hiperbola normalnya. Namun jika kita bekerja dengan sumbu fokus vertikal (cabang terbuka dari atas ke bawah), tanda negatif berpindah dari variabel y ke variabel x :
![]()
Emas
![]()
Dan
![]()
adalah, seperti sebelumnya, koordinat pusat hiperbola dan suku-sukunya
![]()
Dan
![]()
keduanya masih merupakan sumbu semi-mayor dan sumbu semi-minor dari hiperbola, meskipun, tidak seperti sebelumnya, keduanya sekarang akan berorientasi secara vertikal dan horizontal.
Persamaan hiperbola kanonik atau tereduksi
Persamaan hiperbola jenis ini sangat mirip dengan persamaan biasa, yang membedakan hanya persamaan kanonik yang digunakan untuk menyatakan hiperbola secara analitis yang berpusat di titik (0,0). Oleh karena itu, kita menggunakan persamaan hiperbola kanonik atau persamaan tereduksi jika pusat hiperbola adalah titik asal koordinat.
Sekarang kita akan menyimpulkan rumus persamaan tereduksi hiperbola dari persamaan biasa:
![]()
Jika pusat hiperbola berada di titik asal koordinat, yaitu titik (0,0), maka persamaan berikut akan selalu benar:
![]()
![]()
Jadi, rumus persamaan kanonik atau tereduksi hiperbola adalah:
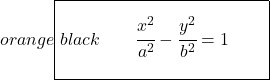
Seperti sebelumnya, jika sumbu fokusnya vertikal dan bukan horizontal, variabel negatifnya adalah x :
![]()
Persamaan umum hiperbola
Rumus persamaan umum hiperbola adalah sebagai berikut:
![]()
Namun, agar persamaan di atas menjadi hiperbola, koefisiennya
![]()
Dan
![]()
Mereka harus berbeda dari nol dan, pada saat yang sama, memiliki tanda yang berlawanan.
Persamaan hiperbola sama sisi
Hiperbola sama sisi adalah hiperbola yang panjang sumbu semi nyata sama dengan panjang sumbu semi imajiner, artinya
![]()
Oleh karena itu, persamaan hiperbola sama sisi adalah:
![]()
Selain itu, asimtot hiperbola sama sisi tegak lurus satu sama lain. Dan persamaan garis-garis tersebut adalah sebagai berikut:
![]()
![]()
Jika kita perhatikan baik-baik, kedua persamaan tersebut masing-masing merupakan garis bagi kuadran pertama (dan ketiga) dan kuadran kedua (dan keempat). Jadi jika kita memutar hiperbola sama sisi sebesar 45° ke kiri, asimtotnya akan menggantikan sumbu koordinat:
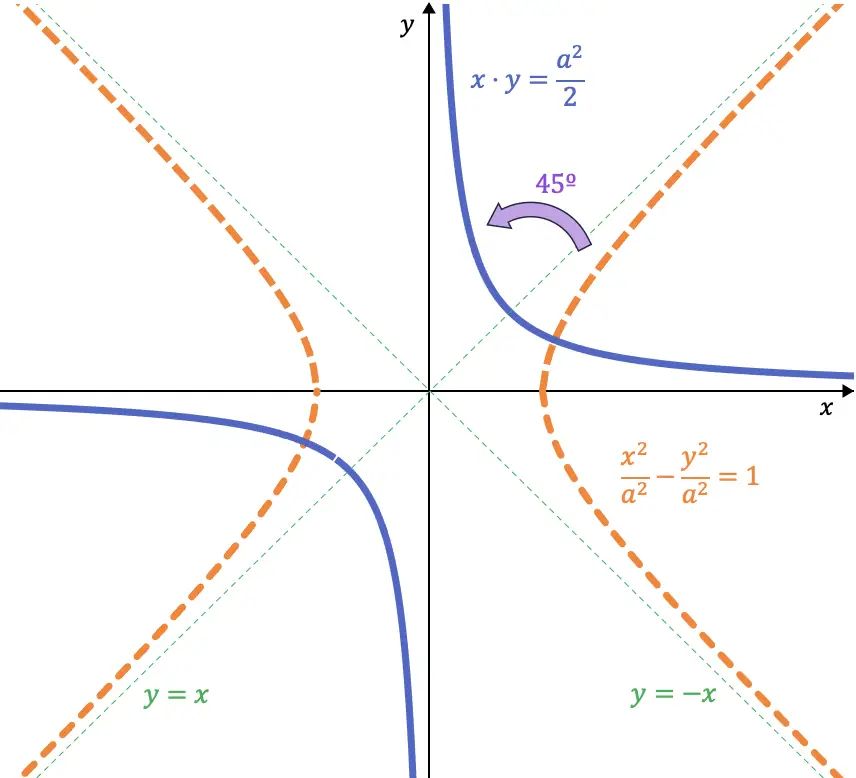
Jadi, ketika kita berbelok 45º, persamaan hiperbolanya adalah:
![]()
hiperbola terkonjugasi
Dua hiperbola terkonjugasi jika sumbu real salah satu hiperbola ekuivalen dengan sumbu imajiner hiperbola lainnya . Oleh karena itu, satu-satunya perbedaan antara persamaan dua hiperbola konjugasi adalah variabel mana yang dinegasikan, karena koefisien penyebutnya harus tetap sama.
Berikut adalah contoh persamaan dua hiperbola yang terkonjugasi satu sama lain:
![]()
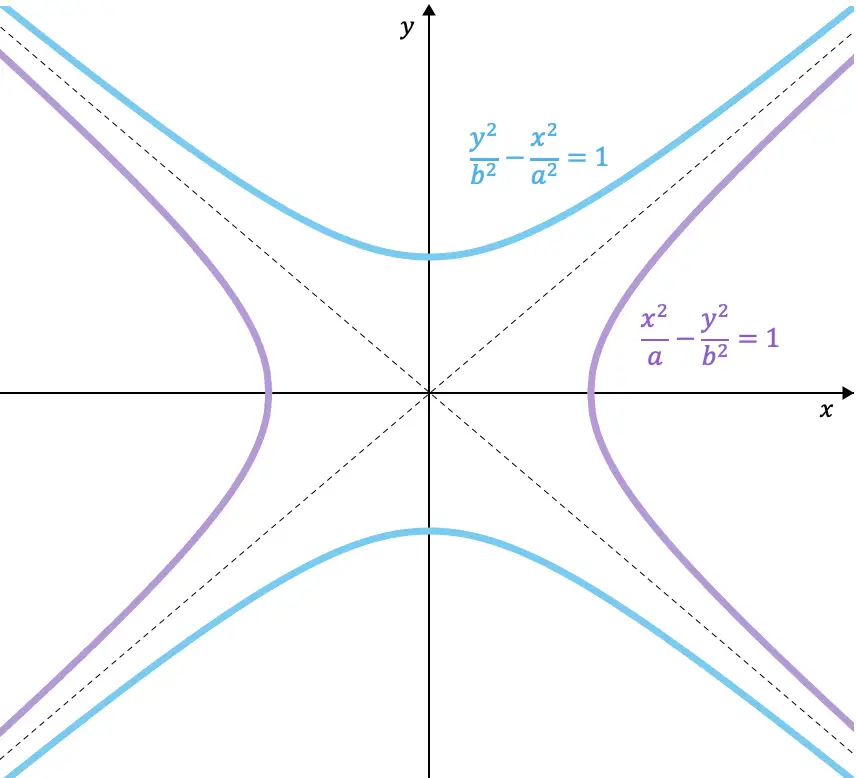
Selain itu, seperti yang Anda lihat dari hiperbola yang telah dibuat grafiknya, hiperbola konjugasi memiliki asimtot yang sama.
Asimtot hiperbola
Seperti yang Anda lihat pada grafik sebelumnya, setiap hiperbola memiliki dua asimtot. Ingatlah bahwa asimtot adalah garis lurus yang sangat dekat dengan suatu fungsi tetapi tidak pernah berpotongan atau menyentuhnya.
Jadi, rumus yang sesuai dengan asimtot hiperbola adalah:
![]()
![]()
Sehingga asimtot hiperbola apa pun dapat dengan mudah ditentukan menggunakan koefisiennya
![]()
Dan
![]()
yang masing-masing merupakan panjang setengah sumbu nyata dan setengah sumbu imajiner hiperbola.
Eksentrisitas hiperbola
Eksentrisitas suatu hiperbola merupakan parameter karakteristik yang menentukan seberapa terbuka atau tertutupnya hiperbola tersebut. Secara numerik, eksentrisitas hiperbola dihitung dengan membagi setengah panjang fokusnya dengan setengah sumbu sebenarnya:
![]()
Eksentrisitas hiperbola apa pun selalu lebih besar dari 1:
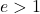
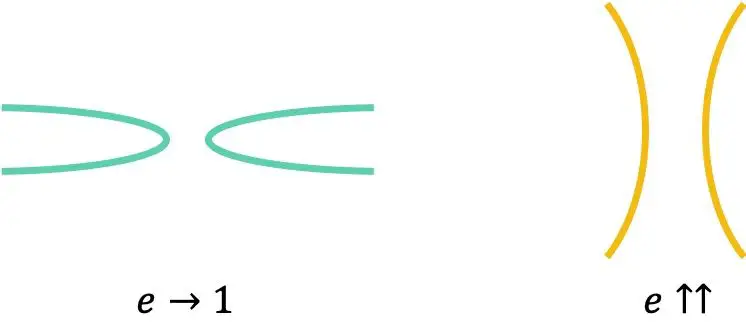
Terakhir, perlu diperhatikan bahwa eksentrisitas hiperbola sama sisi selalu sama dengan
![]()
Masalah hiperbola terpecahkan
Di bawah ini Anda dapat mempraktekkan konsep yang telah kita lihat dengan soal dan menyelesaikan latihan hiperbola dan persamaan hiperbola.
Latihan 1
Berapakah persamaan hiperbola yang berpusat di titik (-1.3), panjang sumbu semi nyata 3 satuan dan panjang sumbu semi khayal (sejajar sumbu Y) 7 satuan?
Untuk mencari persamaan hiperbola, cukup terapkan rumus persamaan biasa hiperbola:
![]()
Kita substitusikan koordinat pusat hiperbola ke dalam persamaan:
![]()
![]()
Dan akhirnya, kami mengganti nilai-nilai yang tidak diketahui
![]()
Dan
![]()
![]()
![]()
Latihan 2
Tentukan koordinat pusat, titik sudut, fokus, nilai eksentrisitas, dan asimtot hiperbola yang persamaannya ditentukan oleh:
![]()
Pertama-tama perlu diperhatikan bahwa variabel negatif pada persamaan tersebut adalah variabel y , sehingga cabang hiperbola akan terbuka ke kanan dan kiri (sumbu fokus sejajar sumbu X).
Kedua, persamaan tersebut sesuai dengan persamaan hiperbola kanonik (atau tereduksi), sehingga pusatnya adalah titik asal koordinat.
![]()
Setelah kita mengetahui pusat hiperbola, untuk menghitung semuanya kita perlu mencari nilai sumbu semi nyata (parameter
![]()
) dan setengah sumbu imajiner (parameter
![]()
). Kita dapat menyimpulkan keduanya dari rumus persamaan hiperbola kanonik (atau tereduksi):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Jadi jika jarak antara pusat dan titik sudut adalah 5 satuan, maka titik sudut hiperbola tersebut adalah:
![]()
Untuk menentukan koordinat setiap titik fokus, Anda harus mengetahui nilai setengah panjang fokus (parameter
![]()
). Dan untuk ini, kita bisa menggunakan rumus yang menghubungkan unsur-unsur hiperbola:
![]()
![]()
![]()
Oleh karena itu terdapat jarak 13 unit antara pusat dan rumah. Jadi, koordinat masing-masing rumah tangga adalah:
![]()
Kemudian, untuk menghitung eksentrisitas hiperbola, kita perlu menggunakan rumus yang sesuai:
![]()
Dan terakhir, kita menemukan asimtot hiperbola dengan rumusnya:
![]()
![]()
Latihan 3
Hitung persamaan hiperbola yang berpusat di titik asal koordinat dengan mengetahui selisih jarak titik hiperbola ke fokus F(-4.0) dan F(4.0) adalah 6 satuan.
Pertama, karena hiperbola berpusat di titik asal koordinat, kita akan menggunakan persamaan kanonik atau persamaan tereduksi:
![]()
Maka menurut definisi hiperbola, nilai absolut selisih jarak salah satu titiknya ke fokus (dalam hal ini adalah 6) harus sama dengan panjang sumbu sebenarnya (
![]()
). Belum:
![]()
![]()
![]()
![]()
Sebaliknya pusat hiperbola adalah titik (0,0) dan fokusnya adalah titik (4,0). Sehingga jarak ke dua titik (parameter
![]()
) sebanyak 4 satuan.
![]()
Sekarang kita dapat mengetahui nilai parameternya
![]()
dengan hubungan matematis antara 3 koefisien karakteristik hiperbola:
![]()
![]()
![]()
![]()
Jadi persamaan hiperbolanya adalah:
![]()
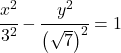
![]()