Parabola (matematika): definisi, persamaan, unsur, contoh,…

Di halaman ini Anda akan menemukan segala sesuatu tentang parabola: apa itu parabola, apa yang diwakilinya, elemen-elemennya (fokus, direktriks, titik sudut, dll.), persamaannya (dengan berbagai jenis persamaan parabola), contoh, latihan yang diselesaikan, propertinya, aplikasinya,…

Apa itu perumpamaan?

Parabola merupakan suatu konsep yang mempunyai arti yang sangat berbeda-beda, namun definisi matematisnya adalah sebagai berikut:

Dalam matematika, parabola adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tetap (disebut fokus) dan garis tetap (disebut direktriks).

Oleh karena itu, setiap titik pada parabola mempunyai jarak yang sama dari fokus dan direktriksnya.

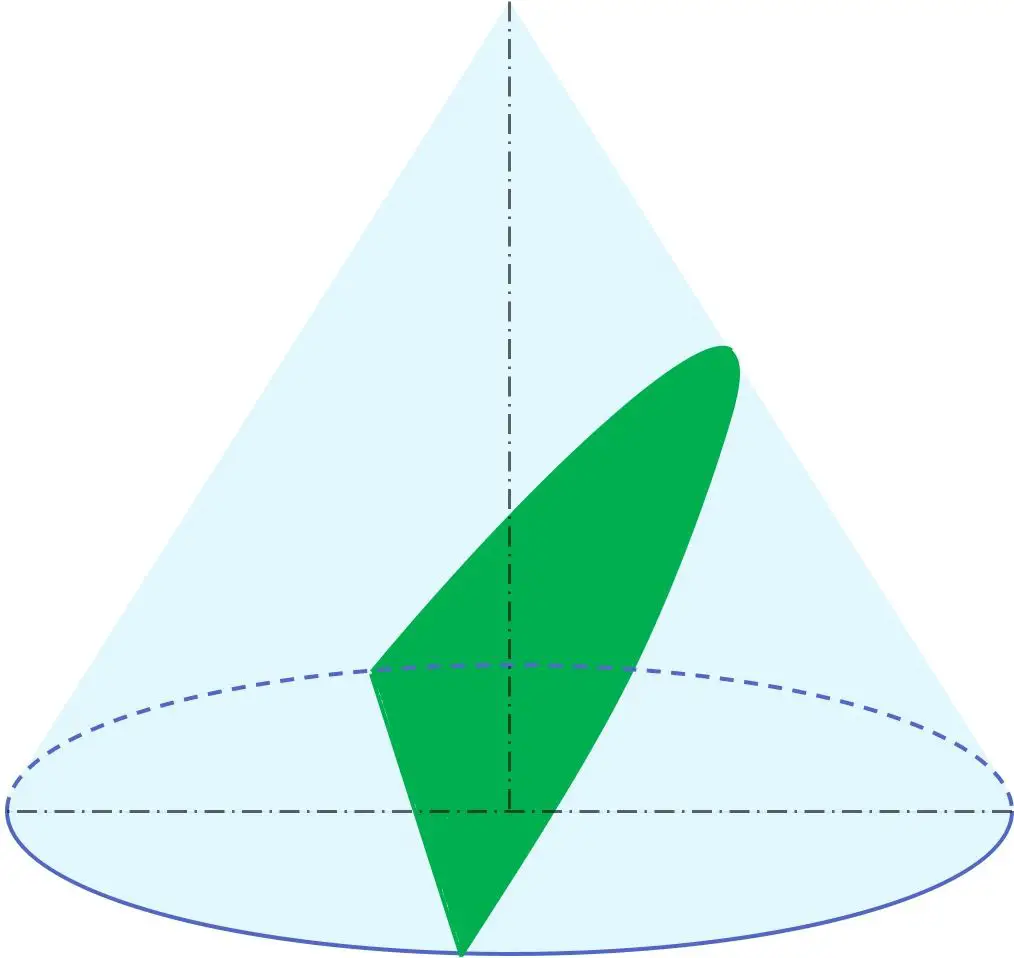
Selain itu, dalam geometri, parabola merupakan salah satu bagian berbentuk kerucut bersama dengan keliling, elips, dan hiperbola. Dengan kata lain, parabola dapat diperoleh dari sebuah kerucut.

Secara khusus, parabola dihasilkan dari potongan kerucut oleh bidang dengan sudut kemiringan relatif terhadap sumbu revolusi yang setara dengan sudut generator kerucut. Oleh karena itu, bidang yang memuat parabola sejajar dengan generator kerucut.

Elemen parabola

Ciri-ciri parabola bergantung pada unsur-unsur berikut:

Fokus (F) : adalah titik tetap di dalam parabola. Jarak titik mana pun pada parabola ke fokus sama dengan jarak dari titik tersebut ke direktriks parabola.
Directrix (D) : merupakan garis tetap di luar parabola. Suatu titik pada parabola mempunyai jarak yang sama dari direktriks dengan jarak dari fokus parabola.
Parameter (p) : adalah jarak fokus ke sutradara.
Vektor radius (R) : adalah ruas yang menghubungkan suatu titik parabola dengan fokus. Nilainya bertepatan dengan jarak dari titik ke direktriks.
Sumbu (E) : adalah garis tegak lurus direktriks yang melalui fokus dan merupakan sumbu simetri parabola, pada grafik di bawah ini sesuai dengan sumbu komputer (sumbu Y). Disebut juga sumbu fokus.
Titik Titik (V) : adalah titik potong antara parabola dan sumbunya.
Panjang fokus : adalah jarak antara fokus dan titik sudut, atau antara direktriks dan titik sudut. Nilainya selalu sama
$\displaystyle \frac{p}{2}.$

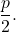
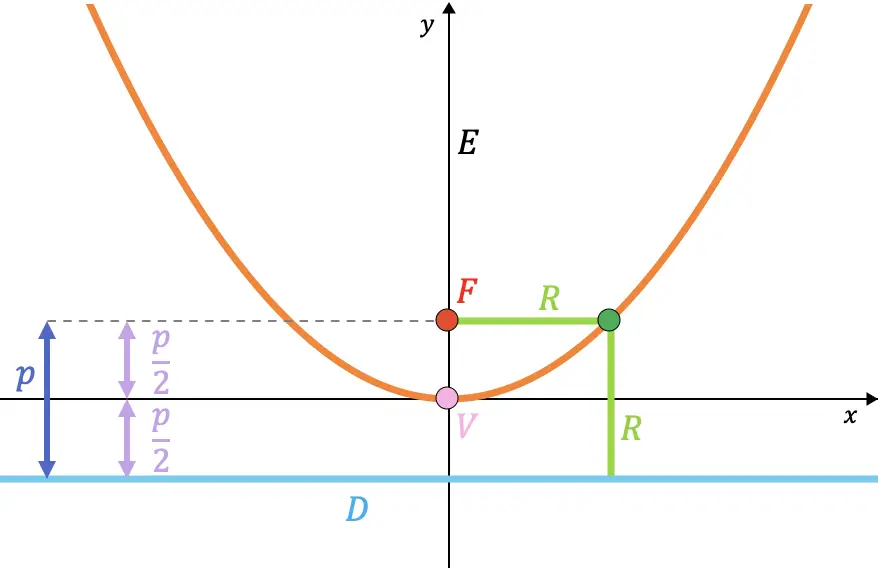
sisi kanan

Sisi kanan parabola adalah tali busur di dalam parabola yang melalui titik fokus dan sejajar dengan direktriks.

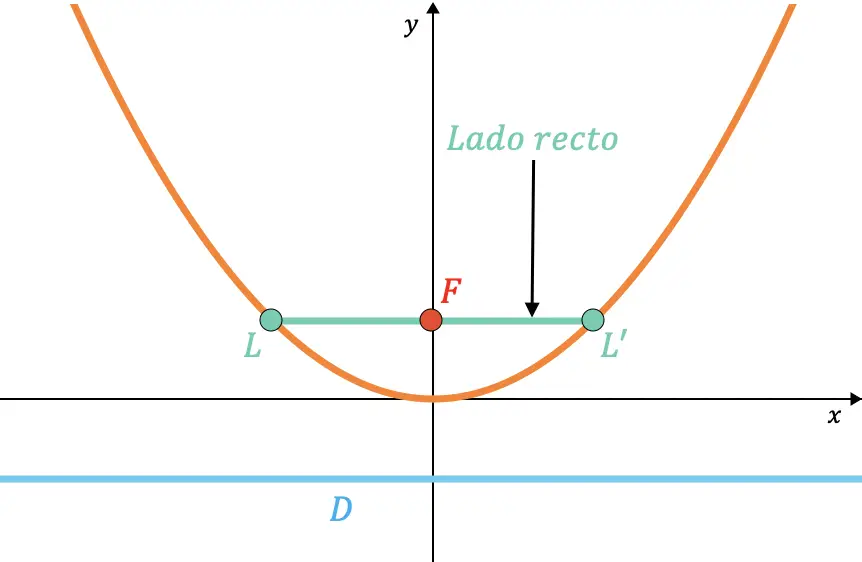
Demikian pula dapat ditunjukkan bahwa panjang sisi kanan selalu dua kali nilai parameternya

$p.$

$\lvert LL'\rvert = 2p$

Sebaliknya, dua garis singgung parabola yang melalui ujung-ujung sisi kanannya membentuk sudut 45º dengan sisi kanannya sendiri dan juga berpotongan di puncak parabola.

persamaan parabola

Persamaan parabola termasuk salah satu jenis fungsi kuadrat karena harus selalu mempunyai minimal 1 suku kuadrat. Selain itu, persamaan parabola bergantung pada orientasi horizontal atau vertikalnya.

Jadi, dalam geometri analitik, ada beberapa cara untuk menyatakan parabola secara matematis: persamaan kanonik atau persamaan tereduksi , persamaan biasa , dan persamaan umum parabola.

Persamaan parabola tereduksi atau kanonik

Yang membedakan persamaan tereduksi atau kanonik dengan persamaan parabola lainnya adalah titik puncak parabola merupakan titik asal koordinat yaitu titik (0,0).

Bentuk persamaan tereduksi parabola bergantung pada apakah persamaan tersebut horizontal atau vertikal. Lihatlah representasi grafis berikut di mana 4 kemungkinan varian ditunjukkan:

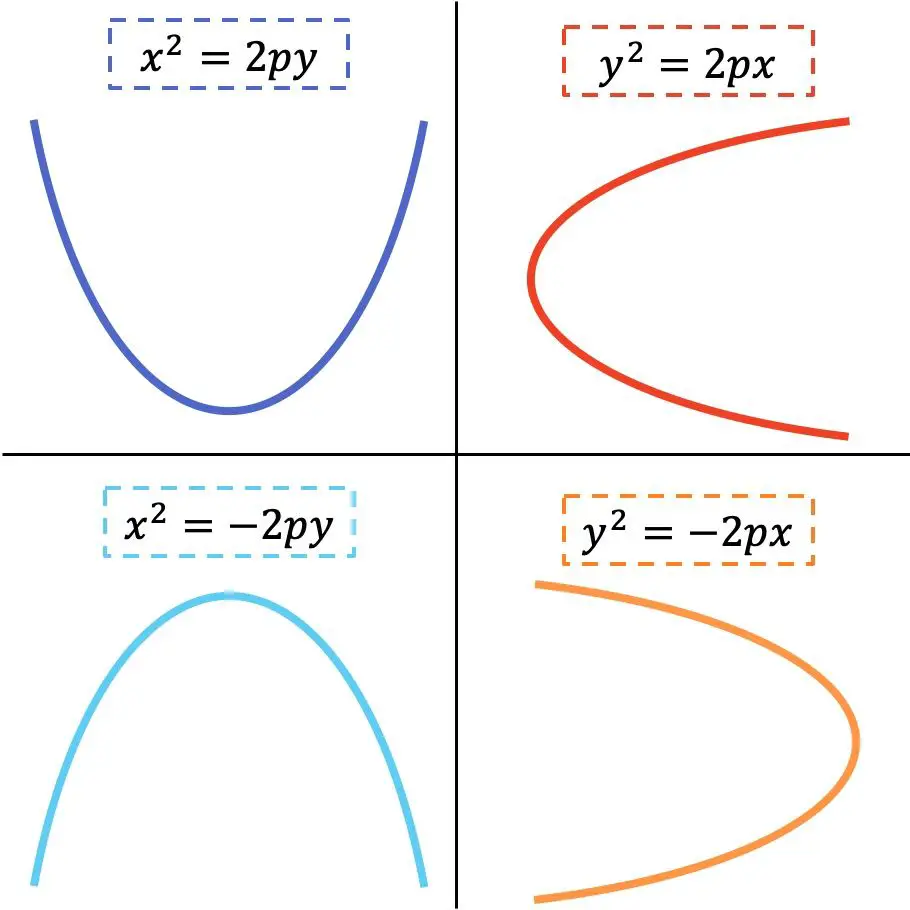
Emas

$p$

adalah parameter karakteristik parabola.

Seperti terlihat pada gambar sebelumnya, jika variabel x dikuadratkan maka parabolanya vertikal, sebaliknya jika variabel y dikuadratkan maka parabolanya horizontal. Sebaliknya, arah cabang parabola bergantung pada tanda persamaan.

Persamaan biasa parabola

Kita baru saja melihat seperti apa persamaan parabola jika titik sudut atau pusatnya sesuai dengan titik asal koordinat (persamaan tereduksi atau kanonik), tetapi bagaimana persamaan parabola jika titik sudut berada di luar titik asal?

Jika titik puncak parabola adalah titik mana pun, kita menggunakan persamaan biasa parabola , yang ekspresinya adalah:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

dimana pusat atau titik puncak parabola adalah titiknya

$V(x_0,y_0).$

Persamaan sebelumnya sesuai dengan parabola yang berorientasi vertikal, yaitu sumbu fokus parabola sejajar dengan sumbu Y.

Demikian pula untuk mendefinisikan parabola yang berorientasi horizontal (sumbu fokusnya sejajar dengan sumbu X), kita harus menggunakan varian persamaan biasa parabola berikut:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Dimana seperti sebelumnya, pusat atau titik puncak parabola adalah titiknya

$V(x_0,y_0).$

Persamaan umum parabola

Sejauh ini semua persamaan parabola yang telah kita analisis digunakan untuk menyatakan parabola horizontal atau vertikal. Tapi yang jelas parabola juga bisa miring atau miring .

Nah, untuk menyatakan parabola jenis ini kita menggunakan persamaan umum parabola yang rumusnya sebagai berikut:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

Persamaan di atas adalah parabola jika dan hanya jika koefisiennya

$A$

Dan

$C$

tidak sekaligus nol dan, terlebih lagi, kondisi berikut terpenuhi:

$B^2-4AC =0$

Contoh cara mencari titik sudut, fokus, dan arah parabola dari persamaannya

Dalam banyak latihan dan soal parabola, Anda diminta menghitung titik sudut, fokus, dan direktriks parabola tertentu. Oleh karena itu, mari kita lihat bagaimana hal ini dilakukan melalui sebuah contoh:

Tentukan titik sudut, fokus, dan direktriks parabola berikut:

$x^2 = 4y$

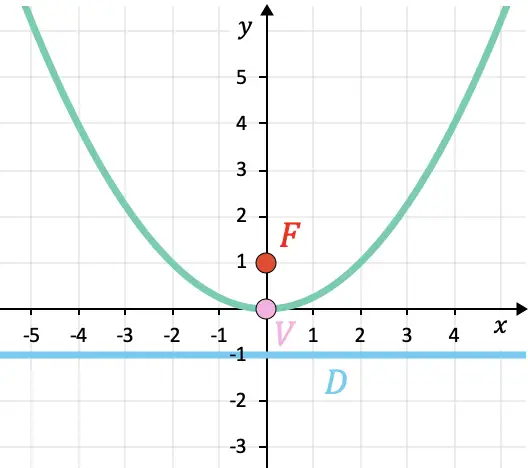
Hal mendasar untuk menyelesaikan masalah parabola jenis ini adalah menentukan parameter p parabola . Dalam hal ini, persamaan parabola sesuai dengan persamaan tereduksi atau kanonik (parabola vertikal):

$x^2 = 2py$

Oleh karena itu, parameter p adalah:

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

Sebaliknya, karena parabola mengikuti persamaan tereduksi atau persamaan kanonik, berarti titik puncak atau pusatnya berada di titik asal koordinat:

$\bm{V(0,0)}$

Setelah kita mengetahui titik sudut dan nilai parameter parabola, kita dapat dengan mudah mencari fokus dan direktriksnya.

Suku kuadrat persamaan tersebut adalah variabel x sehingga sumbu parabola sejajar dengan sumbu OY dan faktanya, karena titik puncaknya adalah titik (0,0), sumbu parabola adalah OY sumbu itu sendiri. Maka titik fokus parabola selalu terletak pada sumbu parabola dan berjarak

$p/2$

dari puncak parabola, maka koordinatnya adalah:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

Demikian pula, pedomannya adalah garis horizontal yang berada pada jarak tertentu

$p/2$

dari titik puncak parabola yang merupakan titik asal koordinat. Oleh karena itu, persamaan garisnya adalah:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

Parabola telah digambarkan di bawah ini sehingga Anda dapat memeriksa hasilnya:

menyelesaikan latihan persamaan parabola

Sifat parabola

Semua parabola mempunyai sifat sebagai berikut:

Parabola merupakan suatu kurva terbuka, atau dengan kata lain terdiri dari dua cabang yang tidak mempunyai titik-titik yang sama dan memanjang tanpa batas.
Setiap parabola mempunyai sumbu simetri yang unik, dimana titik puncak parabola tersebut berada.
Parabola yang berorientasi vertikal berbentuk cembung ketika cabang-cabangnya mengarah ke atas; sebaliknya parabola berbentuk cekung jika cabang-cabangnya mengarah ke bawah.
Eksentrisitas parabola setara dengan kesatuan (1). Eksentrisitas adalah suatu koefisien yang dalam hal ini dihitung dengan membagi jarak fokus ke pusat parabola dengan jarak dari titik sudut ke direktriks (dan kedua jarak tersebut selalu berimpit nilainya).
Dari sifat sebelumnya dapat disimpulkan bahwa semua parabola adalah sebangun atau sebangun.
Parabola tidak mempunyai asimtot.

aplikasi parabola

Sekarang setelah Anda sudah familiar dengan arti sebuah perumpamaan, Anda mungkin bertanya-tanya…apa gunanya sebuah perumpamaan?

Meskipun bagi Anda tidak tampak seperti itu, bentuk geometris parabola sangat umum dalam kehidupan nyata. Misalnya saja saat melempar bola sering terjadi gerakan parabola, terutama pada permainan bola basket. Nah, persamaan parabola sangat berguna untuk mempelajari secara analitis jalur parabola yang dilalui bola.

Penerapan lain dari antena parabola (karena itu dinamakan antena parabola). Karena setiap sinar yang jatuh pada suatu benda berbentuk parabola sejajar sumbu simetri dipantulkan langsung ke fokus, yaitu semua sinar yang menuju antena parabola terkonsentrasi pada fokus dan ini dapat digunakan dengan cara yang berbeda. Inilah sebabnya mengapa fokus sebuah perumpamaan sangat penting.

Memperbaiki masalah hidangan

Latihan 1

Hitung titik sudut, fokus dan direktriks parabola yang persamaannya sebagai berikut:

$y^2 = 8x$

lihat solusi

Pertama, parabola akan berbentuk horizontal karena mengikuti ekspresi persamaan parabola tereduksi atau kanonik berikut ini:

$y^2 = 2px$

Jadi parameter pnya adalah:

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

Sebaliknya, karena parabola mengikuti persamaan tereduksi atau persamaan kanonik, berarti titik puncak atau pusatnya berada di titik asal koordinat:

$\bm{V(0,0)}$

Setelah kita mengetahui nilai titik sudut dan parameter parabola, kita dapat dengan mudah menghitung fokus dan direktriksnya.

Suku kuadrat dari persamaan tersebut adalah variabel, yaitu sumbu parabola akan sejajar dengan sumbu OX dan, faktanya, karena titik puncaknya adalah titik (0,0), l Sumbu parabola adalah sumbu OX itu sendiri. Maka titik fokus parabola selalu terletak pada sumbu parabola dan berjarak

$p/2$

dari puncak parabola yang koordinatnya adalah:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

Demikian pula pedomannya berada pada jarak

$p/2$

dari titik puncak parabola yang merupakan titik asal koordinat dan tegak lurus sumbu fokusnya. Oleh karena itu, persamaan garis pengarahnya adalah:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Latihan 2

Tentukan titik sudut, fokus, dan direktriks parabola yang persamaannya sebagai berikut:

$(x-4)^2 = -16(y+1)$

lihat solusi

Parabola didefinisikan menurut persamaan biasa (sumbu sejajar sumbu Y), yang rumusnya adalah:

$(x-x_0 )^2 = 2p (y-y_0)$

Jadi parameter pnya adalah:

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

Sebaliknya dalam hal ini persamaan biasa parabola mengandung arti bahwa pusatnya tidak berada pada titik asal koordinat, sebaliknya koordinat kartesius titik puncak parabola adalah bilangan-bilangan dalam tanda kurung yang telah diubah tandanya. :

$\bm{V(4,-1)}$

Setelah kita mengetahui nilai titik sudut dan parameter parabola, kita dapat menghitung fokus dan direktriksnya.

Suku kuadrat persamaan tersebut adalah variabel x sehingga sumbu parabola sejajar dengan sumbu OY. Jadi, fokus parabola selalu terletak pada sumbu parabola dan berjarak

$p/2$

dari titik puncak parabola, sehingga koordinat titik fokusnya sama dengan titik titik tersebut dengan menjumlahkan

$p/2$

Tegak lurus:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

Demikian pula, direktriksnya adalah garis horizontal yang letaknya agak jauh

$p/2$

dari puncak parabola. Oleh karena itu, persamaan garis pengarahnya adalah:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Latihan 3

Tentukan persamaan parabola yang sumbunya sejajar sumbu absis, mempunyai titik V(5,2) sebagai titik puncaknya dan fokusnya di titik P(8,2).

lihat solusi

Dalam hal ini titik puncak parabola bukanlah titik asal koordinat, sehingga diperlukan persamaan biasa untuk menentukan parabola pernyataan tersebut. Selain itu, sumbu fokus parabola sejajar dengan sumbu x, artinya parabola akan berorientasi horizontal (cabangnya akan mengarah ke kanan atau ke kiri) dan oleh karena itu suku kuadrat dari persamaan tersebut haruslah variabel. kamu :

$(y-y_0 )^2 = 2p (x-x_0)$