Perkalian matriks

Pada halaman ini kita akan melihat cara mengalikan matriks berdimensi 2×2, 3×3, 4×4, dst. Kami menjelaskan prosedur perkalian matriks langkah demi langkah melalui sebuah contoh, kemudian Anda akan menemukan latihan yang terselesaikan sehingga Anda juga dapat berlatih. Terakhir, Anda akan mengetahui kapan dua matriks tidak dapat dikalikan dan semua properti operasi matriks tersebut.

Bagaimana cara mengalikan dua matriks?

Mari kita lihat tata cara melakukan perkalian dua matriks dengan contoh:

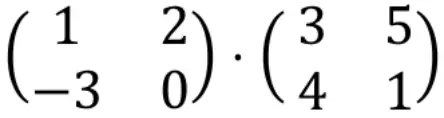
contoh cara mengalikan dua matriks berdimensi 2x2, operasi dengan matriks

Untuk menghitung perkalian matriks, baris matriks kiri harus dikalikan dengan kolom matriks kanan.

Jadi pertama-tama kita perlu mengalikan baris pertama dengan kolom pertama. Caranya, kita mengalikan setiap elemen pada baris pertama dengan setiap elemen pada kolom pertama satu per satu, dan menjumlahkan hasilnya. Jadi semua ini akan menjadi elemen pertama dari baris pertama array yang dihasilkan. Lihatlah prosedurnya:

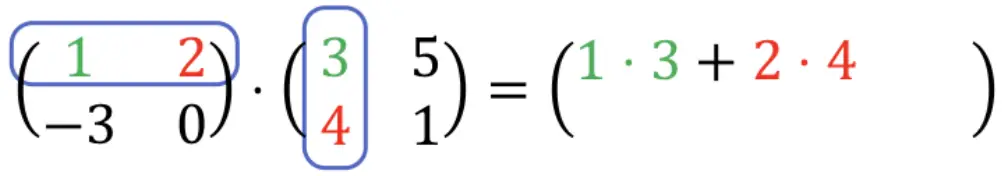
cara menyelesaikan perkalian matriks 2x2, operasi dengan matriks

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Jadi:

Sekarang kita perlu mengalikan baris pertama dengan kolom kedua . Oleh karena itu, kami mengulangi prosedurnya: kami mengalikan setiap elemen pada baris pertama satu per satu dengan setiap elemen pada kolom kedua, dan kami menjumlahkan hasilnya. Dan semua ini akan menjadi elemen kedua dari baris pertama array yang dihasilkan:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Jadi:

Setelah kita mengisi baris pertama dari matriks yang dihasilkan, kita berpindah ke baris kedua. Oleh karena itu, kita mengalikan baris kedua dengan kolom pertama dengan mengulangi prosedur ini: kita mengalikan satu per satu setiap elemen baris kedua dengan setiap elemen kolom pertama, dan menjumlahkan hasilnya:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Belum:

Terakhir, kita kalikan baris kedua dengan kolom kedua . Selalu dengan prosedur yang sama: kita mengalikan setiap elemen baris kedua satu per satu dengan setiap elemen kolom kedua, dan kita menjumlahkan hasilnya:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Belum:

Dan disinilah perkalian kedua matriks tersebut berakhir. Seperti yang Anda lihat, Anda perlu mengalikan baris dengan kolom, selalu mengulangi prosedur yang sama: kalikan setiap elemen baris dengan setiap elemen kolom satu per satu, dan tambahkan hasilnya.

Latihan perkalian matriks terpecahkan

Latihan 1

Selesaikan perkalian matriks berikut:

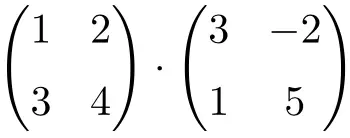
latihan menyelesaikan perkalian langkah demi langkah matriks 2x2, operasi dengan matriks

Ini adalah produk dari matriks orde 2:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}

Untuk menyelesaikan perkalian matriks, Anda harus mengalikan baris matriks kiri dengan kolom matriks kanan.

Jadi kita kalikan dulu baris pertama dengan kolom pertama. Caranya, kita mengalikan setiap elemen pada baris pertama dengan setiap elemen pada kolom pertama satu per satu, dan menjumlahkan hasilnya. Dan semua ini akan menjadi elemen pertama dari baris pertama array yang dihasilkan:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}

Sekarang mari kalikan baris pertama dengan kolom kedua, untuk mendapatkan elemen kedua dari baris pertama matriks yang dihasilkan:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}

Kita menuju ke baris kedua, jadi kita mengalikan baris kedua dengan kolom pertama:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}

Terakhir, kita mengalikan baris kedua dengan kolom kedua , untuk menghitung elemen terakhir tabel:

\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}

Jadi hasil perkalian matriksnya adalah:

\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}

Latihan 2

Carilah hasil perkalian matriks persegi 2×2 berikut:

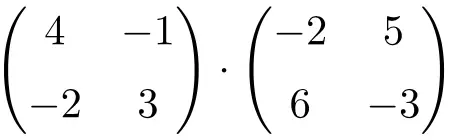
Latihan diselesaikan selangkah demi selangkah dalam perkalian matriks 2x2, operasi matriks

Ini adalah hasil kali matriks berdimensi 2×2.

Untuk menyelesaikan perkalian, Anda harus mengalikan baris matriks kiri dengan kolom matriks kanan:

\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}

Latihan 3

Hitung perkalian matriks 3×3 berikut:

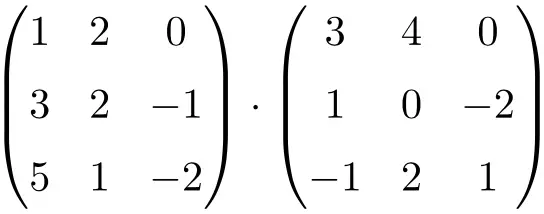
latihan menyelesaikan perkalian matriks 3x3 langkah demi langkah, operasi matriks

Untuk melakukan perkalian matriks 3×3, Anda harus mengalikan baris matriks kiri dengan kolom matriks kanan:

\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}

Latihan 4

diberikan matriks

A

:

\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}

Menghitung:

\displaystyle 2A\cdot A^t

Pertama-tama kita akan menghitung matriks transpos dari

A

untuk melakukan perkalian. Dan untuk membuat matriks transpose, kita perlu mengubah baris menjadi kolom. Artinya, baris pertama matriks menjadi kolom pertama matriks dan baris kedua matriks menjadi kolom kedua matriks. Belum:

\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}

Oleh karena itu, operasi matriksnya tetap:

\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}

Sekarang kita bisa melakukan perhitungan. Kita hitung dulu

2A

(walaupun kita juga bisa menghitungnya terlebih dahulu

A \cdot A^t

):

\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =

\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}

Dan terakhir, kita menyelesaikan perkalian matriks:

\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =

\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}

Latihan 5

Perhatikan matriks berikut:

\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}

Menghitung:

\displaystyle A\cdot B - B \cdot A

Ini adalah operasi yang menggabungkan pengurangan dengan perkalian matriks orde 2:

\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}

Pertama-tama kita hitung perkaliannya di sebelah kiri:

\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =

\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}

Sekarang kita selesaikan perkalian di sebelah kanan:

\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =

\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}

Dan terakhir kita kurangi matriksnya:

\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =

\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}

Kapan dua matriks tidak bisa dikalikan?

Tidak semua matriks dapat dikalikan. Untuk mengalikan dua matriks, jumlah kolom pada matriks pertama harus sama dengan jumlah baris pada matriks kedua.

Misalnya perkalian berikut tidak dapat dilakukan karena matriks pertama mempunyai 3 kolom dan matriks kedua mempunyai 2 baris:

\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}

Tapi kalau kita membalik urutannya, jumlahnya bisa berlipat ganda. Karena matriks pertama mempunyai dua kolom dan matriks kedua mempunyai dua baris:

\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}

Sifat Perkalian Matriks

Jenis operasi matriks ini memiliki ciri-ciri sebagai berikut:

  • Perkalian matriks bersifat asosiatif:

\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)

  • Perkalian matriks juga mempunyai sifat distributif:

\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C

  • Hasil kali matriks tidak bersifat komutatif:

\displaystyle A \cdot B \neq B \cdot A

Misalnya perkalian matriks berikut memberikan hasil:

\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}

Namun hasil perkaliannya akan berbeda jika kita membalik urutan perkalian matriksnya:

\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}

  • Selain itu, matriks apa pun dikalikan dengan matriks identitas akan menghasilkan matriks yang sama. Ini disebut sifat identitas perkalian:

\displaystyle A \cdot I=A

\displaystyle I \cdot A=A

Misalnya:

\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}

  • Terakhir, seperti yang sudah Anda duga, matriks apa pun dikalikan dengan matriks nol sama dengan matriks nol. Ini disebut sifat perkalian dari nol:

\displaystyle A \cdot 0=0

\displaystyle 0\cdot A=0

Misalnya:

\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}

Tinggalkan Komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *

Scroll to Top