Matriks nilpoten - Mathoritas

Di halaman ini Anda akan menemukan penjelasan tentang apa itu matriks nilpoten, serta beberapa contohnya agar Anda dapat memahaminya dan tidak ragu lagi. Selain itu, Anda akan dapat melihat struktur matriks nilpoten dan semua properti dari jenis matriks tersebut.

Apa itu matriks nilpoten?

Pengertian matriks nilpoten adalah sebagai berikut:

Matriks nilpoten adalah matriks persegi yang dipangkatkan menjadi bilangan bulat menghasilkan matriks nol .

$N^k =0$

Emas

$N$

adalah matriks nilpoten dan

$k$

eksponen pangkat yang menghasilkan matriks nol.

Kondisi ini bukan berarti pangkat matriks nilpoten selalu bernilai nol berapa pun eksponennya, melainkan jika terdapat paling sedikit satu pangkat matriks yang hasilnya matriks penuh 0, maka matriks tersebut nilpoten.

Sebaliknya, indeks nilpotensi dari matriks nilpotensi adalah bilangan terkecil yang memenuhi kondisi nilpotensi. Kita juga dapat mengatakan bahwa matriks nilpoten berorde k , di mana k adalah indeks nilpotensinya.

Contoh matriks nilpoten

Untuk menyelesaikan pemahaman konsep matriks nilpoten, kita akan melihat beberapa contoh matriks jenis ini:

Contoh matriks nilpoten 2×2

Matriks persegi berdimensi 2×2 berikut ini nilpoten:

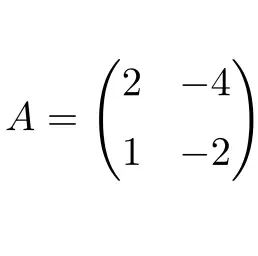
Matriks tersebut nilpoten karena dengan mengkuadratkan matriks A kita memperoleh matriks nol sebagai hasilnya:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

Oleh karena itu, matriks tersebut merupakan matriks nilpoten dan indeks nihilpotensinya adalah 2, karena matriks nol diperoleh pangkat dua.

Contoh matriks nilpoten 3×3

Matriks persegi berorde 3 berikut ini nilpoten:

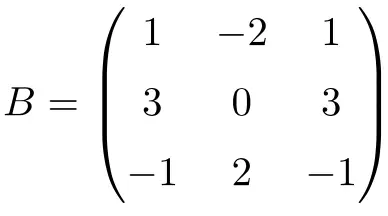
Meskipun dengan menaikkan matriks menjadi 2 kita tidak mendapatkan matriks nol:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Tetapi ketika menghitung pangkat tiga suatu matriks, kita mendapatkan matriks yang semua elemennya sama dengan 0:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Jadi matriks B adalah matriks nilpoten, dan karena matriks nol dipangkatkan 3, maka indeks nilpotensinya adalah 3.

Struktur matriks nilpoten 2 × 2

Di bawah ini Anda dapat melihat struktur semua matriks nilpoten. Pembuktiannya agak membosankan, jadi kami langsung memberikan rumus untuk mendapatkan matriks nilpoten orde 2:

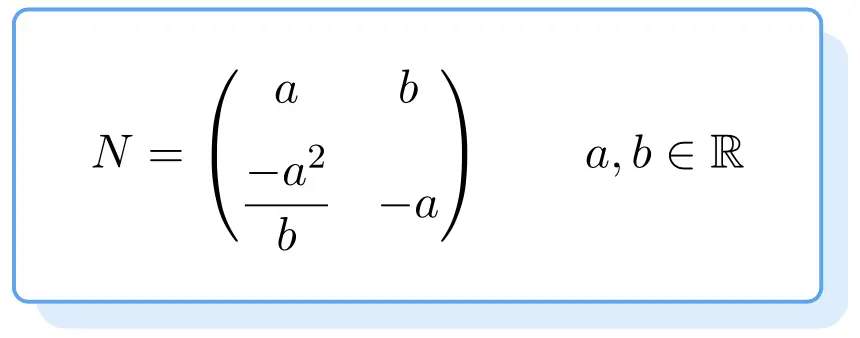
Jadi matriks apa pun yang memenuhi rumus di atas akan menjadi matriks nilpoten. Untuk ini, nilai-nilainya

$a$

Dan

$b$

bilangan tersebut dapat berubah-ubah selama bilangan tersebut merupakan bilangan real.

Sifat-sifat matriks nilpoten

Matriks nilpoten mempunyai ciri-ciri sebagai berikut:

Jejak matriks nilpoten selalu nol.

Demikian pula determinan suatu matriks nilpoten selalu sama dengan 0. Namun hal sebaliknya tidak benar, yaitu determinan suatu matriks adalah nol tidak berarti matriks tersebut nilpoten.

Satu-satunya matriks nilpoten yang dapat didiagonalisasi adalah matriks nol.

Indeks nilpotensi matriks nilpoten berdimensi n×n selalu sama dengan atau kurang dari n . Inilah sebabnya mengapa indeks nilpotensi dari matriks nilpoten 2 × 2 akan selalu sama dengan 2.

Matriks nilpoten tidak dapat dibalik.

Matriks segitiga apa pun yang diagonal utamanya nol juga merupakan matriks nilpoten.

Ada teorema yang menyatakan bahwa jika matriks
$N$

nilpoten, maka matriksnya

$N+I$

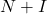
dapat dibalik, di mana

$I$

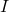
adalah matriks identitas. Selain itu, matriks inversnya dapat dicari dengan rumus berikut:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

Sama halnya jika
$N$

adalah matriks nilpoten, maka invers matriks tersebut dapat dihitung

$N-I$

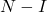
dengan persamaan berikut:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Matriks tunggal apa pun, artinya tidak dapat dibalik, dapat didekomposisi menjadi hasil kali matriks nilpoten.

Semua nilai eigen (atau nilai eigen) dari matriks nilpoten adalah nol.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Terakhir, yang membuat penasaran, ada juga konsep transformasi nihilpoten, yang mendefinisikan aplikasi linier
$L$

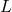
dari ruang vektor sedemikian rupa sehingga

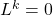
$L^k=0$

.

Matriks nihil