Posisi relatif dua garis pada bidang

Di halaman ini Anda akan menemukan penjelasan berbagai metode yang ada untuk menentukan posisi relatif dua garis pada bidang (di R2). Selain itu, Anda akan melihat beberapa contoh dan Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah.

Berapakah kedudukan relatif dua garis pada bidang tersebut?

Sebelum melihat posisi relatif antara dua garis pada suatu bidang, tentunya anda perlu mengetahui secara pasti apa itu garis, hal tersebut dapat anda temukan pada definisi garis .

Jadi, ketika bekerja dalam dua dimensi (dalam R2), ada 3 jenis kemungkinan posisi relatif antara dua garis:

garis-garis yang berpotongan

kedudukan relatif dua garis yang berpotongan

Dua garis yang berpotongan hanya mempunyai satu titik yang sama.

Garis sejajar

Dua garis dikatakan sejajar jika tidak mempunyai titik persekutuan. Artinya, jika mereka tidak pernah berpapasan.

garis yang bertepatan

posisi relatif dari garis-garis yang berhimpitan

Dua garis dikatakan sama jika semua titiknya sama.

Sebaliknya, sudut antara dua garis pada bidang juga bergantung pada posisi relatifnya:

Garis berpotongan berpotongan pada sudut antara 0º (tidak termasuk) dan 90º (inklusif). Selain itu, jika membentuk sudut siku-siku 90º saja, berarti kedua garis tersebut tegak lurus.
Garis sejajar membentuk sudut 0º karena arahnya sama.
Dan, untuk alasan yang sama, garis-garis yang berhimpitan juga membentuk sudut 0º di antara keduanya.

Jika Anda ingin mengetahui cara menghitung sudut antara dua garis, Anda bisa melihat rumus sudut antara dua garis . Di sini Anda akan menemukan penjelasan detail tentang cara menentukan sudut antara dua garis, serta beberapa contoh bahkan latihan soal agar Anda dapat berlatih dan memahami konsepnya secara maksimal.

Cara mencari kedudukan relatif dua garis pada bidang

Mengetahui posisi relatif antara dua garis dalam ruang dua dimensi bergantung pada cara garis tersebut dinyatakan:

Vektor arah garis: jika dua garis mempunyai vektor arah yang berbeda, maka keduanya harus berpotongan. Sebaliknya, jika koordinat vektor arahnya sama atau sebanding, keduanya bisa sejajar atau berimpit (perlu diperiksa apakah keduanya mempunyai titik yang sama).

Persamaan eksplisit: ketika dua garis mempunyai kemiringan yang berbeda
$(m)$

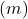
mereka mengering Sebaliknya jika garis mempunyai kemiringan yang sama tetapi urutannya berbeda di titik asal

$(n)$

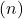
mereka paralel. Terakhir, dua garis tertukar padahal awalnya mempunyai kemiringan dan ordinat yang sama.

Persamaan umum (atau implisit): dua garis dengan koefisien nonproporsional A dan B akan selalu berpotongan. Akan tetapi, ketiga suku tersebut akan sejajar jika kedua parameter tersebut sebanding satu sama lain tetapi tidak sebanding dengan koefisien C. Dan, terakhir, jika ketiga suku tersebut sebanding, hal ini berarti garis-garis tersebut tertukar.

Jika anda masih ragu dengan persamaan garis di atas, anda bisa membaca penjelasan persamaan garis pada bidang . Di sini Anda akan menemukan rumus semua persamaan garis, cara menghitungnya, contoh dan latihan penyelesaian persamaan garis.

Dalam tabel berikut Anda memiliki ringkasan properti sebelumnya:

Selanjutnya, kita akan melihat dua contoh cara menentukan posisi relatif antara dua garis:

Contoh 1

Temukan posisi relatif antara dua garis berikut yang didefinisikan dalam bentuk persamaan eksplisit:

$r: \ y=3x+2 \qquad \qquad s: \ y=3x-4$

Kedua garis mempunyai kemiringan yang sama:

$m_r = m_s = 3$

Tetapi mereka memiliki komputer yang berbeda pada awalnya:

$n_r =2\neq n_s=-4$

Jadi, karena kemiringannya sama tetapi titik potongnya berbeda, maka garis-garis tersebut sejajar .

Contoh 2

Tentukan posisi relatif antara dua garis berikut yang dinyatakan dengan persamaan implisit (atau umum):

$r: \ 4x+2y-6=0 \qquad \qquad s: \ -2x-y+3=0$

Kedua garis dinyatakan sebagai persamaan eksplisit, oleh karena itu kita perlu melihat apakah ada koefisien yang sebanding:

$\cfrac{4}{-2}=\cfrac{2}{-1} = \cfrac{-6}{3} = -2$

Ketiga suku garis tersebut sebanding, jadi kedua garis tersebut berimpit .

Tentukan kedudukan relatif dua garis pada bidang dengan sistem persamaan

Cara lain untuk mengetahui posisi relatif antara dua garis adalah dengan menganalisis sistem persamaan yang dibentuk oleh persamaan garis:

Jika sistem mempunyai solusi unik , garis-garisnya berpotongan. Selanjutnya titik potong kedua garis tersebut merupakan penyelesaian sistem.
Jika suatu sistem tidak mempunyai penyelesaian , hal ini menunjukkan bahwa garis-garis tersebut tidak mempunyai titik-titik yang sama sehingga merupakan garis-garis sejajar.
Jika sistem mempunyai solusi yang tak terhingga banyaknya , ini berarti semua garis mempunyai titik-titik yang sama dan oleh karena itu merupakan garis-garis yang berpotongan.

Contoh 3

Hitung posisi relatif dua garis berikut dengan menggunakan sistem persamaan:

$r: \ 3x+4y+5=0 \qquad \qquad s: \ 5x+y-3=0$

Untuk mencari posisi relatif kedua garis, kita perlu menyelesaikan sistem persamaan linear yang dibentuk oleh kedua garis berikut:

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}$

Dalam hal ini kita akan menyelesaikan sistem tersebut dengan metode substitusi. Oleh karena itu kami akan mengisolasi variabel tersebut

$y$

dari persamaan kedua dan substitusikan ke persamaan pertama:

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}$

$3x+4(3-5x)+5=0$

$3x+12-20x+5=0$

$3x-20x=-12-5$

$-17x=-17$

$x=\cfrac{-17}{-17} = 1$

Dan begitu kita tahu betapa berharganya hal yang tidak diketahui itu

$x$

Kami mengganti nilainya ke dalam ekspresi yang ditemukan

$y:$

$y=3-5x \ \xrightarrow{x \ = \ 1} \ y = 3 -5\cdot 1$

$y = 3 -5 = -2$

Oleh karena itu kita hanya memperoleh satu penyelesaian dari sistem persamaan yang terdiri dari dua garis tersebut, sehingga kedua garis tersebut berpotongan . Dan titik perpotongannya adalah solusi sistem, yaitu titik

$(1,-2).$

Menyelesaikan masalah kedudukan relatif dua garis pada bidang

Latihan 1

Tentukan apakah garis-garis berikut berpotongan, sejajar, atau berimpit:

$r: \ 3x-y+4=0 \qquad \qquad s: \ 9x-3y+3=0$

lihat solusi

Kedua garis dinyatakan sebagai persamaan implisit (atau umum), oleh karena itu kita perlu melihat apakah ada koefisien yang proporsional:

$\cfrac{3}{9}=\cfrac{-1}{-3} \neq \cfrac{4}{3}$

Hanya koefisien A dan B pada garis-garis yang sebanding satu sama lain, dan tidak sebanding dengan koefisien C. Oleh karena itu , kedua garis tersebut sejajar .

Latihan 2

Temukan posisi relatif antara dua garis berikut yang dinyatakan sebagai persamaan parametrik:

$\displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}$

lihat solusi

Kita dapat menyelesaikan sistem persamaan yang dibentuk oleh dua garis untuk mencari posisi relatifnya. Namun karena berbentuk persamaan parametrik, vektor arahnya dapat dengan mudah dicari dan jika tidak proporsional berarti garis-garisnya berpotongan. Dan dalam hal ini, kita tidak akan menghabiskan banyak waktu untuk menyelesaikan keseluruhan sistem persamaan.

Sehingga koordinat kartesius vektor arah tiap garis adalah angka di depan parameternya

$t:$

$\vv{r} =(-5,3) \qquad \qquad \vv{s}=(-2,9)$

Setelah kita mengetahui vektor arahnya, kita periksa proporsionalitasnya:

$\cfrac{-5}{-2} \neq \cfrac{3}{9}$

Vektor-vektor arahnya tidak sebanding, oleh karena itu garis-garisnya saling bersilangan .

Latihan 3

Tunjukkan apakah garis-garis berikut berpotongan, sejajar atau berhimpitan dan temukan juga titik potong di antara keduanya (jika ada).

$r: \ y=4x-5 \qquad \qquad s: \ y=-2x+7$

lihat solusi

Kedua garis tersebut ditentukan oleh persamaan eksplisitnya dan memiliki kemiringan yang berbeda:

$m_r =4 \neq m_s = -2$

Karena kemiringannya berbeda, garis-garisnya berpotongan .

Oleh karena itu, karena garis-garis tersebut berpotongan maka keduanya akan mempunyai 1 titik persekutuan dan untuk menghitungnya kita harus menyelesaikan sistem persamaan yang dibentuk oleh kedua garis tersebut:

$\left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}$

Dalam hal ini kita akan menyelesaikan sistem dengan metode pemerataan karena keduanya

$y$

sudah dihapus:

$y=y$

$4x-5=-2x+7$

$4x+2x=5+7$

$6x=12$

$x=\cfrac{12}{6} = 2$

Dan begitu kita menghadapi hal yang tidak diketahui

$x$

kami mengganti nilainya dengan ekspresi apa pun

$y$

untuk mengetahui berapa nilainya:

$y=4x-5$

$y = 4\cdot 2 -5 = 8 -5 = 3$

Jadi titik potong kedua garis tersebut merupakan hasil sistem :

$\bm{(2,3)}$

Latihan 4

Hitung nilai yang tidak diketahui

$a$

Dan

$b$

sehingga dua garis berikut sejajar:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

lihat solusi

Garis-garis tersebut dijelaskan dalam bentuk persamaan umum (atau implisit). Oleh karena itu, agar kedua garis sejajar maka koefisien A dan Bnya harus proporsional, yaitu persamaan berikut harus dipenuhi:

$\cfrac{2}{1} = \cfrac{-4}{a}$

Oleh karena itu kita harus menyelesaikan persamaan sebelumnya untuk mendapatkan nilai yang tidak diketahui

$a.$

Untuk melakukan ini, kita mengalikan pecahan secara melintang:

$2 \cdot a = -4 \cdot 1$

$a = \cfrac{-4}{2}$

$\bm{a=-2}$

Sebaliknya, agar garis-garis sejajar, suku-suku independennya tidak dapat sebanding dengan koefisien lainnya:

$\cfrac{2}{1} \neq \cfrac{6}{b}$

Oleh karena itu, seperti sebelumnya, kita menyelesaikan pertidaksamaan dengan mengalikan pecahan secara melintang:

$2 \cdot b \neq 6 \cdot 1$

$b \neq \cfrac{6}{2}$

$\bm{b\neq 3}$

Singkatnya, agar kedua garis tersebut sejajar

$a$

harus 2 dan

$b$

dapat berupa bilangan real apa pun kecuali 3.

Latihan 5

Temukan persamaan eksplisit garis yang sejajar dengan garis tersebut

$r$

dan apa yang terjadi di titik tersebut

$P(3,-1).$

menjadi lurus

$r:$

$r: \; y=2x+5$

lihat solusi

Sehingga garis tersebut sejajar dengan garis

$r,$

keduanya harus mempunyai kemiringan yang sama. dan kemiringan garis

$r$

adalah 2:

$m = 2$

Oleh karena itu, persamaan garis yang perlu kita cari adalah:

$y=2x+n$

Dan setelah kita mengetahui kemiringan garis, kita dapat menghitung perpotongan y dengan mensubstitusikan titik yang termasuk dalam garis tersebut ke dalam persamaan garis:

$P(3,-1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=-1} \ -1=2\cdot 3 +n$

$-1=6+ n$

$-1-6= n$

$-7= n$

Jadi persamaan garisnya secara eksplisit adalah:

$\bm{y=2x-7}$

Jika Anda sudah sampai sejauh ini, berarti Anda sudah menguasai posisi relatif antara dua garis dalam denah. Bagus sekali!

Namun satu hal yang membuat banyak orang bertanya-tanya adalah…dan apa gunanya mengetahui posisi relatif antara dua garis?

Nah, salah satu penerapan posisi relatif antar garis adalah untuk dapat mengetahui jarak antara 2 garis, karena perhitungan jarak dua garis bergantung pada posisi relatifnya:

Jika garis-garis tersebut berpotongan atau berimpit maka jaraknya nol.
Sebaliknya, jika garisnya sejajar, rumus tertentu harus diterapkan. Jika Anda lebih tertarik, Anda bisa melihat cara menghitung jarak antara dua garis sejajar .

Berapakah kedudukan relatif dua garis pada bidang tersebut?

Cara mencari kedudukan relatif dua garis pada bidang

Contoh 1

Contoh 2

Tentukan kedudukan relatif dua garis pada bidang dengan sistem persamaan

Contoh 3

Menyelesaikan masalah kedudukan relatif dua garis pada bidang

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Tinggalkan Komentar Batalkan Balasan