Di halaman ini kami menjelaskan apa itu perkalian campuran tiga vektor (atau perkalian titik tiga) dan cara menghitungnya. Anda juga akan melihat contoh, latihan, dan penyelesaian masalah pada jenis operasi antar vektor ini. Dan, sebagai tambahan, Anda akan menemukan sifat dan kegunaan produk campuran.
Berapakah hasil kali campuran tiga buah vektor?
Hasil kali campuran tiga vektor, disebut juga hasil kali tiga titik , adalah perkalian berurutan antara tiga vektor yang melibatkan dua jenis operasi berbeda: hasil kali titik dan hasil kali vektor . Jadi, kombinasi kedua operasi vektor menghasilkan skalar (bilangan real).
Konkretnya, perkalian campuran terdiri dari penghitungan perkalian vektor dari dua vektor dan selanjutnya mengalikan hasil yang diperoleh secara vektor dengan vektor ketiga. Ditulis seperti ini mungkin terlihat sangat rumit, namun kenyataannya tidak terlalu banyak, lihat rumus perkalian triple dot:
![]()
Seperti yang Anda lihat dalam rumusnya, hasil kali campuran tiga vektor ditunjukkan dengan dua tanda kurung siku.
Bagaimana cara menghitung hasil kali campuran tiga vektor?
Rumus hasil kali tiga titik adalah rumus yang baru saja kita lihat di bagian sebelumnya, namun umumnya tidak digunakan untuk menentukan hasil kali campuran tiga vektor karena ada cara lain yang lebih sederhana dan cepat:
Misalkan 3 vektor apa pun menjadi:
![]()
Untuk menghitung hasil kali campuran antara tiga vektor, cukup selesaikan determinan 3×3 yang dibentuk oleh komponen-komponen vektor tersebut:
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fed933d4d02bb5ca6f5bae06ea544d_l3.png)
Jadi Anda dapat melihat contoh cara menghitungnya , kita akan menemukan hasil kali campuran dari tiga vektor berikut:
![]()
Untuk menentukan hasil kali campuran, kita membuat determinan orde 3 dengan menempatkan vektor-vektor pada baris matriks:
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5341b4a39b42c1284a4b0129b38b61a_l3.png)
Dan sekarang kita hanya perlu menyelesaikan determinan matriksnya, untuk ini Anda dapat menggunakan metode apa pun. Dalam hal ini, kita akan menerapkan aturan Sarrus (tetapi ini juga dapat dilakukan dengan penjumlahan atau kofaktor):
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df86565048cf897265878936f2294525_l3.png)
Untuk menunjukkan bahwa kedua prosedur tersebut ekuivalen, kita akan menghitung hasil kali campuran vektor-vektor yang sama melalui definisinya:
![Rendered by QuickLaTeX.com \begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4d15d610ca9b4cb39e9f268cfb152ae_l3.png)
Kami menyarankan untuk menghitung hasil perkalian campuran melalui determinan vektor, karena lebih cepat dan kecil kemungkinan terjadinya kesalahan. Namun, seperti yang Anda lihat, hasilnya tetap sama, apa pun metode yang Anda gunakan, jadi gunakan metode mana pun yang Anda suka. 👍
Interpretasi geometris dari produk campuran
Setelah Anda mengetahui cara mencari hasil kali campuran dari tiga vektor, Anda mungkin bertanya-tanya…dan untuk apa hasil kali campuran tersebut? Nah, dalam matematika ada dua kegunaan utama: menghitung volume paralelepiped dan volume tetrahedron.
Volume suatu parallelepiped sama dengan nilai mutlak hasil kali campuran vektor-vektor yang menandai 3 dimensi bidang geometri.
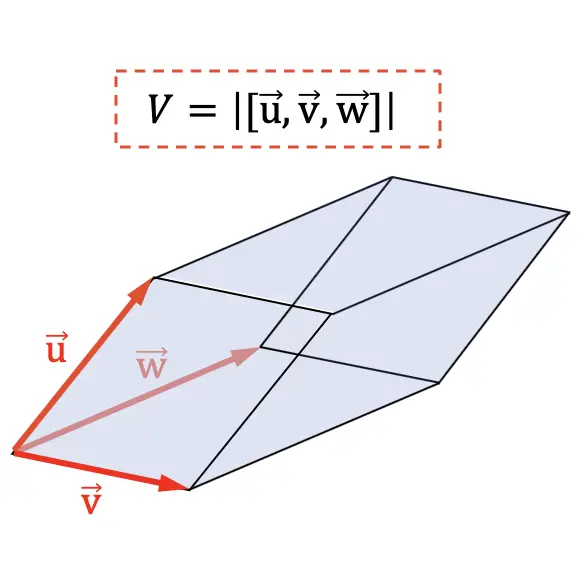
Penerapan lain dari produk campuran adalah untuk menentukan volume tetrahedron . Karena secara geometris seperenam nilai mutlak hasil kali campuran mewakili volume tetrahedron:
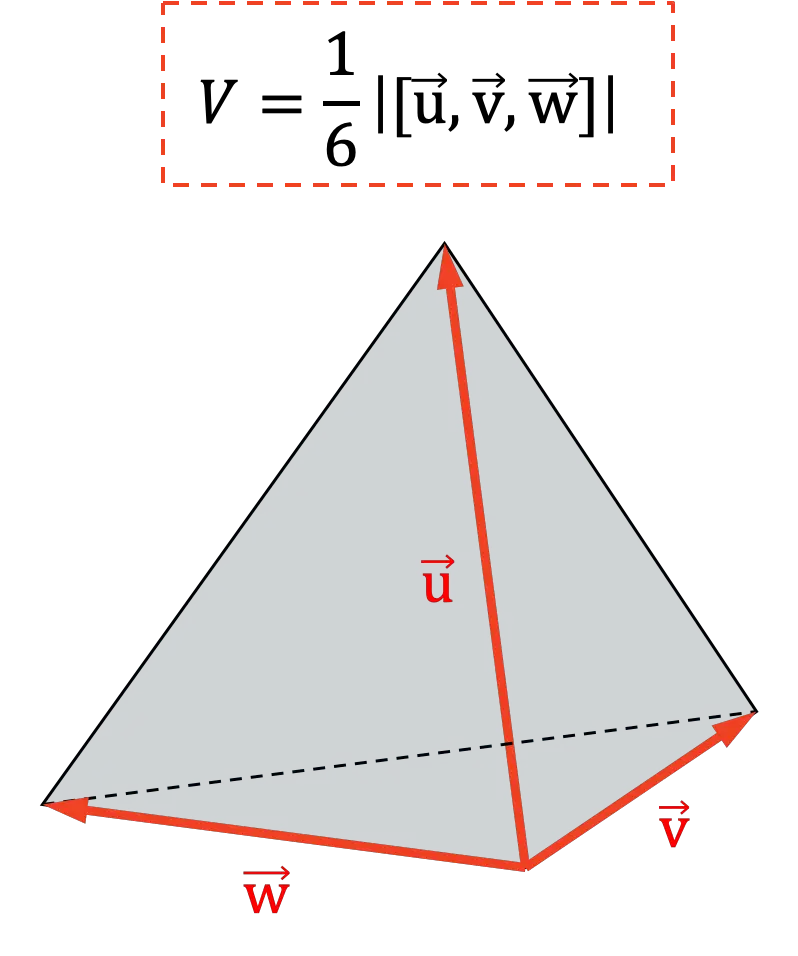
Sifat-sifat produk campuran atau produk triple dot
Produk campuran, atau produk skalar rangkap tiga, memiliki ciri-ciri sebagai berikut:
- Secara umum, perubahan orde vektor hasil kali campuran juga mengakibatkan perubahan tanda. Oleh karena itu, urutan vektor hasil kali campuran menjadi penting.
![]()
- Namun, jika kita mengubah urutannya secara siklis , tandanya tidak berubah:
![]()
- Dalam ruang tiga dimensi (dalam R3), hasil kali campuran tiga vektor bergantung linier atau vektor koplanar (yang berada pada bidang yang sama) sama dengan 0.
Memperbaiki masalah produk campuran
Latihan 1
Diberikan 3 vektor:
![]()
Hitung hasil kali campuran ketiga vektor:
![]()
Untuk mencari hasil kali campurannya, kita harus menyelesaikan determinan yang terdiri dari koordinat vektor-vektornya:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-549ed90889d541ae4a1075449567b062_l3.png)
Latihan 2
Diberikan 3 vektor:
![]()
Tentukan hasil kali campuran antara ketiga vektor:
![]()
Untuk mencari hasil kali campurannya, kita perlu mencari determinan yang mempunyai koordinat kartesius vektor-vektornya dalam bentuk garis:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29b46155243552a99f6fd75de69f59da_l3.png)
Latihan 3
Hitunglah volume suatu bangun datar yang ketiga sisinya merupakan vektor berikut:
![]()
Volume suatu parallelepiped sama dengan nilai absolut hasil kali campuran 3 vektor yang dimilikinya sebagai rusuk. Oleh karena itu, pertama-tama kita menghitung perkalian silang rangkap tiga dari vektor-vektor tersebut:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9718b369a508216fbb69ab68ac7de381_l3.png)
Sehingga volume parallelepiped merupakan nilai absolut dari hasil perkalian campuran:
![]()
Latihan 4
Hitunglah volume tetrahedron yang titik sudutnya berada pada titik-titik berikut:
![]()
Pertama, kita menghitung vektor yang mewakili tepi tetrahedron:
![]()
![]()
![]()
Volume tetrahedron setara dengan seperenam nilai absolut hasil kali campuran 3 vektor yang dimilikinya untuk sisi-sisinya. Oleh karena itu, pertama-tama kita menghitung hasil kali campuran dari vektor-vektor yang ditemukan:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d384e76415a756b834e0a8e7c695b1c1_l3.png)
Jadi volume tetrahedron akan menjadi seperenam dari nilai absolut produk campuran:
![]()