Garis berpotongan - Mathority

Di halaman ini Anda akan menemukan segala sesuatu tentang garis potong: apa artinya, jenis-jenis berbeda yang ada, cara mengetahui apakah dua garis merupakan garis potong, cara menemukan titik persekutuannya,… Anda juga akan dapat melihat beberapa contoh dan latihan yang diselesaikan dari garis potong.

Apa yang dimaksud dengan dua garis yang berpotongan?

Dalam matematika, pengertian garis potong adalah sebagai berikut:

Dua garis berpotongan jika berpotongan di satu titik saja. Oleh karena itu, garis-garis yang berpotongan hanya mempunyai satu titik yang sama. Selain itu, dua garis yang berpotongan tentu harus berada pada bidang kartesius yang sama.

Konsep dua garis yang berpotongan pada satu titik penting dilakukan karena jika terdapat lebih dari satu titik potong maka keduanya merupakan garis yang berhimpitan, sebaliknya jika tidak mempunyai titik potong maka keduanya merupakan garis sejajar.

Contoh garis berpotongan

Setelah kita melihat arti dari dua garis yang berpotongan, sekarang mari kita lihat 2 contoh berbeda dari jenis garis ini:

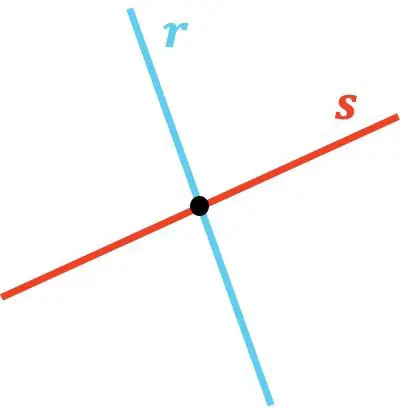
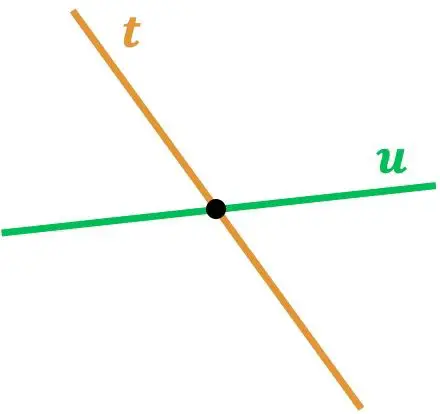
Seperti yang Anda lihat, garis r dan s berpotongan karena bersinggungan di satu titik. Demikian pula, garis t memotong garis u karena ada titik perpotongannya.

Jenis garis berpotongan

Ada dua jenis garis berpotongan:

Garis tegak lurus : adalah garis yang berpotongan tegak lurus 90º.
Garis miring: terdiri dari garis-garis yang berpotongan pada sudut lancip antara 0º dan 90º (tidak termasuk).

Garis lurus tegak lurus

Garis tegak lurus adalah garis yang berpotongan membentuk empat sudut 90 derajat.

Demikian pula kemiringan dua garis yang tegak lurus selalu memenuhi syarat berikut:

$m_r = -\cfrac{1}{m_s}$

Sifat lain dari garis-garis yang berpotongan tegak lurus adalah hasil kali titik antara vektor-vektor arahnya (vektor yang menunjukkan arah suatu garis) sama dengan nol.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Jika anda lebih tertarik dengan garis tegak lurus, pada link ini anda bisa melihat contoh garis tegak lurus . Selain itu, Anda juga akan menemukan cara menghitung garis yang tegak lurus dengan garis lainnya, sifat-sifat jenis garis tersebut, latihan yang diselesaikan langkah demi langkah, dll.

garis miring

Garis miring adalah garis yang berpotongan membentuk sudut lancip dan sudut tumpul berpasangan. Artinya, buatlah dua sudut lancip (kurang dari 90º) dan dua sudut tumpul (lebih besar dari 90º). Namun menurut pengertian sudut dua garis, sudut antara dua garis adalah sudut terkecil yang dibentuknya.

Sudut antara dua garis miring beserta kemiringannya dapat dihitung dengan menggunakan rumus berikut:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Bagaimana cara mengetahui dua garis berpotongan?

Ada 3 metode utama untuk mencari posisi relatif dua garis:

Dengan vektor arah kedua garis.
Dengan kemiringan kedua garis tersebut.
Dengan persamaan implisit (atau umum) dari dua garis.

Selanjutnya kita simak penjelasan dari 3 cara yang ada untuk mengetahui perpotongan dua garis.

Dari vektor arah garis

Jika koordinat vektor arah (vektor yang menandai arah suatu garis) dari dua garis yang berbeda tidak sebanding , maka kedua garis tersebut berpotongan.

Mari kita lihat latihan yang diselesaikan selangkah demi selangkah dari dua garis yang berpotongan:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Kedua garis tersebut dinyatakan sebagai persamaan parametrik, sehingga komponen vektor arah setiap garis adalah angka di depan parameternya.

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Jadi, untuk melihat apakah vektor-vektor arahnya proporsional, kita perlu membagi koordinatnya. Jika kita memperoleh hasil yang sama pada kedua pembagian, maka keduanya akan proporsional; sebaliknya jika hasilnya berbeda berarti vektor-vektornya tidak proporsional.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

Pembagian komponen-komponennya tidak ekuivalen, sehingga vektor-vektornya tidak sebanding sehingga garis-garisnya berpotongan.

di awal lereng

Jika dua garis memiliki kemiringan yang berbeda , berarti kedua garis tersebut berpotongan.

Misalnya, dua garis berikut berpotongan karena kemiringannya berbeda:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

Kemiringan garis

$r$

adalah -2 dan kemiringan garis

$s$

adalah 3.

$m_r =-2 \neq m_s =3$

Karena kedua garis tersebut tidak mempunyai kemiringan yang sama maka keduanya berpotongan.

Dari persamaan garis implisit

Dapat juga diketahui apakah dua garis berpotongan atau tidak melalui persamaan implisit (atau persamaan umum) garis tersebut. Persamaan implisit garis tersebut adalah sebagai berikut:

$Ax+By+C=0$

Jadi, dua garis berpotongan jika koefisien A dan B tidak sebanding.

Mari kita lihat contoh dua garis berpotongan yang didefinisikan dengan persamaan implisitnya:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Untuk memverifikasi bahwa ini adalah dua garis yang berpotongan, kita harus menganalisis proporsionalitas koefisien A (angka di depan variabel

$x$

) dengan koefisien B (digit di depan variabel

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

Kedua suku tersebut tidak proporsional, sehingga secara efektif kedua garis tersebut berpotongan.

Temukan titik persekutuan dari dua garis yang berpotongan

Seperti yang telah kita lihat, garis-garis yang berpotongan hanya mempunyai satu titik yang sama. Jadi, untuk menghitung titik potong dua garis potong , perlu diselesaikan sistem persamaan yang dibentuk oleh kedua garis tersebut.

Sebagai contoh, kita akan mencari titik potong dua garis berikut:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

Untuk menentukan titik potong kedua garis tersebut, kita harus menyelesaikan sistem persamaan linear yang dibentuk oleh kedua garis tersebut:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

Dalam hal ini kita akan menyelesaikan sistem tersebut dengan metode substitusi. Oleh karena itu kami akan mengisolasi variabel tersebut

$x$

dari persamaan pertama dan substitusikan ke persamaan kedua:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

Dan begitu kita tahu betapa berharganya hal yang tidak diketahui itu

$y$

Kami mengganti nilainya ke dalam ekspresi yang ditemukan

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

Oleh karena itu penyelesaian sistem persamaan tersebut adalah titik potong kedua garis tersebut. Dan poin ini adalah

$\bm{(3,1)}.$

garis yang memotong lingkaran

Biasanya, ketika kita mengatakan bahwa dua garis berpotongan, kita mengacu pada konsep yang baru saja kita lihat. Namun dalam geometri, ada arti lain dari garis potong:

Garis yang berpotongan dengan lingkaran adalah garis yang memotong lingkaran (atau kurva) di dua titik berbeda.

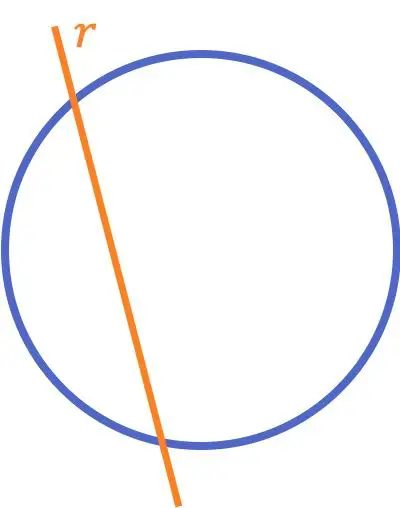
Berbeda dengan konsep dua garis berpotongan yang biasa diajarkan di sekolah dasar, pengertian garis yang berpotongan dengan lingkaran ini sering dipelajari di kelas-kelas selanjutnya beserta semua kedudukan relatif garis dengan lingkaran.