Cara Memfaktorkan Polinomial (Polynomial Factoring) -

Di halaman ini kami menjelaskan cara memfaktorkan semua jenis polinomial. Pertama-tama kita akan melihat cara memfaktorkan suatu polinomial dengan aturan Ruffini, kemudian kita akan melanjutkan ke bagaimana polinomial tanpa suku bebas difaktorkan, kemudian kita akan menganalisis faktorisasi akar polinomial dengan pecahan dan, terakhir, kasus-kasus khusus dari faktorisasi (perhatikan identitas, faktorisasi dengan pengelompokan, trinomial, dll). Semua penjelasan diberikan dengan contoh dan, sebagai tambahan, pada akhirnya Anda akan dapat berlatih dengan latihan yang diselesaikan langkah demi langkah untuk memfaktorkan polinomial.

Apa itu faktorisasi polinomial?

Faktorisasi polinomial adalah teknik yang digunakan dalam matematika untuk menguraikan polinomial menjadi produk faktor.

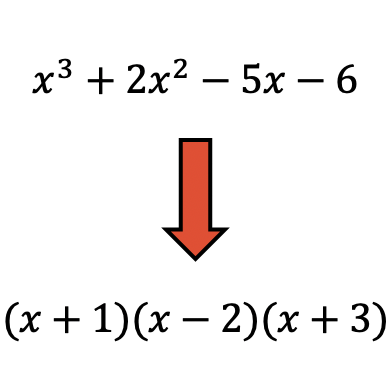
memfaktorkan polinomial (memfaktorkan polinomial)

Memfaktorkan polinomial sangat berguna karena lebih mudah untuk melakukan operasi dengan polinomial yang difaktorkan.

Sekarang setelah kita mengetahui apa itu pemfaktoran polinomial, mari kita lihat bagaimana polinomial difaktorkan.

Cara memfaktorkan polinomial dengan aturan Ruffini

Tentunya untuk memahami cara memfaktorkan polinomial dengan aturan Ruffini, Anda harus terlebih dahulu mengetahui cara menerapkan aturan Ruffini . Jadi kami tinggalkan tautan ini untuk Anda jika Anda ingin meninjau terlebih dahulu seperti apa prosedurnya.

Untuk memfaktorkan polinomial, langkah-langkah berikut harus diikuti:

Akar polinomial dihitung berdasarkan aturan Ruffini.
Setiap akar yang ditemukan bertipe x=a dinyatakan dalam bentuk faktor (xa).
Polinomial terfaktor adalah hasil kali semua faktor yang ditemukan dikalikan dengan koefisien suku derajat tertinggi dari polinomial tak berbobot.

Agar Anda dapat melihat cara kerjanya dan lebih memahami prosedur pemfaktoran polinomial, di bawah ini Anda akan menemukan contoh konkret yang dijelaskan langkah demi langkah:

Faktorkan polinomial berikut:

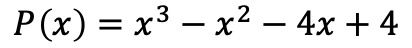
Hal pertama yang harus dilakukan adalah menghitung akar atau nol polinomial. Untuk melakukannya, kita perlu mencari pembagi suku bebas polinomial tersebut , yang dalam hal ini adalah ±1, ±2, dan ±4.

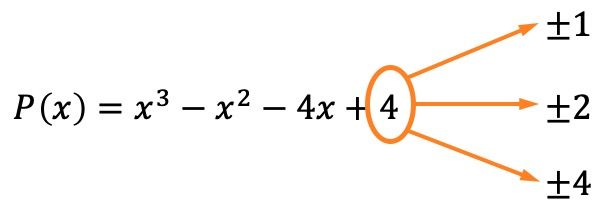
Sekarang kita tahu, berkat teorema sisa dan faktor, bahwa jika sisa pembagian polinomial dengan salah satu nilai tersebut sama dengan 0, berarti nilai tersebut adalah akar dari polinomial tersebut.

Oleh karena itu, kita harus membagi polinomial tersebut dengan masing-masing pembagi suku bebas dengan aturan Ruffini dan melihat dalam kasus mana sisanya adalah nol.

Misalnya kita mulai dengan menerapkan aturan Ruffini dengan

$x=+1:$

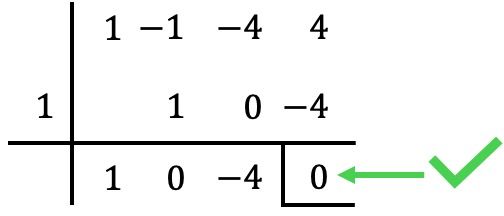
Dalam hal ini, sisa (atau sisa) pembagiannya adalah nol, jadi

$x=1$

Ini adalah akar dari polinomial. ✅

Sempurna, kita sudah memiliki akar polinomialnya, yang tersisa hanyalah menentukan akar-akar lainnya yang tersisa. Untuk melakukan ini, kita menggunakan aturan Ruffini dengan pembagi lain dari suku bebas, misalnya

$x=-1.$

Selain itu, tidak perlu menggunakan metode Ruffini dengan polinomial bilangan bulat, namun kita dapat melanjutkan dari bagian terakhir yang kita tinggalkan pada langkah sebelumnya:

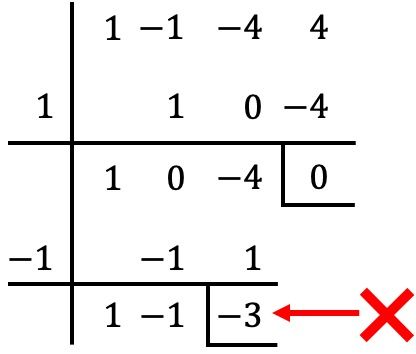
Namun, dalam hal ini, ketika membaginya dengan

$x=-1$

sisa yang diperoleh berbeda dengan 0, jadi

$x=-1$

Ini bukan akar dari polinomial. ❌

Oleh karena itu kita harus mencoba nilai lain, misalnya kita menggunakan aturan Ruffini

$x=+2:$

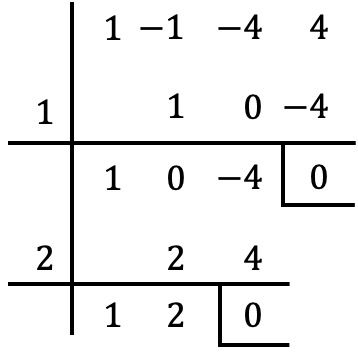
Dalam hal ini kita kembali mendapatkan sisa nol, jadi

$x=2$

Ini juga merupakan akar dari polinomial.

Dan kami terus menerapkan prosedur yang sama. Sekarang kami memeriksa apakah

$x=-2$

apakah itu akar polinomial atau bukan:

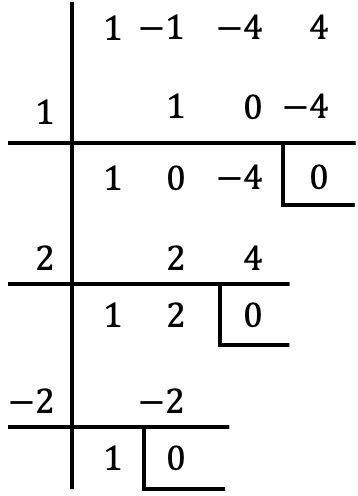
Dengan membaginya dengan

$x=-2$

Dengan aturan Ruffini kita memperoleh sisa nol, jadi

$x=-2$

adalah akar atau nol dari polinomial.

Oleh karena itu kita tidak dapat lagi menerapkan aturan Ruffini, oleh karena itu kita telah menemukan semua akar polinomialnya, yaitu:

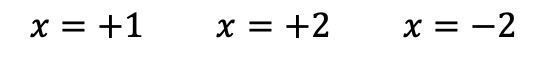
Setelah kita menentukan semua akar polinomial, kita dapat memfaktorkannya. Untuk melakukan ini, cukup ungkapkan setiap akar

$x=a$

dalam bentuk faktor tipenya

$(x-a)$

, artinya untuk setiap akar kata Anda harus memberi tanda kurung dengan a

$x$

dan root telah berubah tanda:

Dan sekarang kita sudah mempunyai semua akar yang dinyatakan sebagai faktor, kita harus mengalikan semua tanda kurung dengan koefisien suku derajat tertinggi dari polinomial asal:

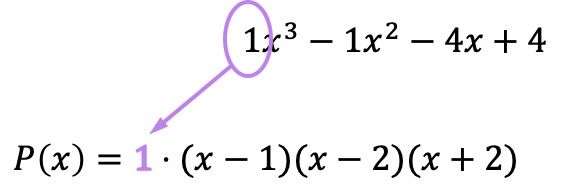
polinomial faktor koefisien derajat tertinggi

Meskipun dalam hal ini koefisiennya adalah 1 sehingga tidak mempengaruhi hasil, penting untuk diingat untuk melakukan perkalian ini. Karena jika koefisien tersebut berbeda dengan 1, maka polinomial yang difaktorkan akan berubah dan oleh karena itu, dengan tidak memasukkan bilangan tersebut kita akan membuat kesalahan dalam memfaktorkan polinomial tersebut.

Singkatnya, polinomial terfaktornya adalah:

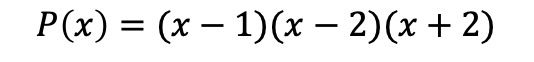
Memfaktorkan polinomial tanpa suku bebas

Kita baru saja melihat bahwa suku independen penting untuk memfaktorkan polinomial, karena suku independen memungkinkan kita mengidentifikasi akar-akar polinomial yang mungkin. Namun, bagaimana cara memfaktorkan polinomial yang tidak memiliki suku bebas?

Untuk memfaktorkan suatu polinomial tanpa suku bebas , pertama-tama kita harus mengekstrak faktor persekutuan dari polinomial tersebut, kemudian mengekstrak akar-akar polinomial tanpa faktor persekutuan tersebut menggunakan aturan Ruffini.

Ditulis seperti ini, mungkin terdengar agak rumit, jadi mari kita selesaikan contohnya langkah demi langkah sehingga Anda dapat melihat cara memfaktorkan polinomial dengan faktor persekutuan:

Lakukan penguraian faktorial dari polinomial berikut:

$P(x) = x^4-3x^3-x^2+3x$

Seperti yang Anda lihat, polinomial dalam soal tidak memiliki suku independen, jadi kita harus mengambil faktor persekutuan dari polinomial tersebut. Jika kita perhatikan lebih dekat, semua elemen polinomial memiliki setidaknya satu

$x,$

jadi faktor persekutuannya adalah

$x.$

Oleh karena itu, ketika mengekstraksi faktor persekutuan dari polinomial, kita mendapatkan ekspresi berikut:

$P(x) = x\left(x^3-3x^2-x+3\right)$

Dan setelah kita mengekstrak faktor persekutuan dari polinomial tersebut, kita menerapkan aturan Ruffini untuk menghitung akar-akar polinomial yang dikelompokkan dalam tanda kurung (dengan prosedur yang kita lihat di bagian sebelumnya):

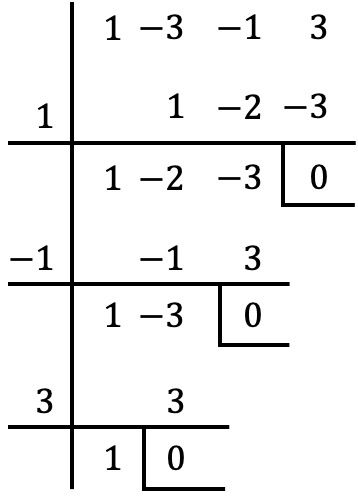
Jadi akar atau nol dari polinomial dalam tanda kurung adalah:

$\bm{x=+1 \qquad x=-1 \qquad x=+3}$

Oleh karena itu, untuk memfaktorkan suatu polinomial, cukup ganti polinomial dalam tanda kurung dengan akar-akarnya dalam bentuk faktor (seperti yang dijelaskan pada bagian di atas):

$\begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}$

Dan dengan cara ini kita telah memfaktorkan polinomial yang tidak mempunyai suku berderajat 0. Perhatikan bahwa satu-satunya perbedaan adalah kita harus mengekstrak faktor persekutuannya terlebih dahulu, tetapi semua langkah berikut ini persis sama.

Di sisi lain, Anda harus mengetahuinya

$x=0$

Ini juga merupakan akar dari polinomial, karena ketika kita mengekstrak faktor persekutuannya, hal ini menyiratkan bahwa salah satu akar dari polinomial tersebut adalah

$x=0.$

Jadi, semua akar polinomialnya adalah sebagai berikut:

$\bm{x= 0 \qquad x=+1 \qquad x=-1 \qquad x=+3}$

Faktanya, polinomial harus memiliki akar sebanyak yang ditunjukkan oleh derajatnya. Dalam hal ini polinomialnya berderajat 4 sehingga mempunyai 4 akar.

Memfaktorkan polinomial dengan akar rasional

Sejauh ini kita telah melihat contoh pemfaktoran polinomial dengan akar bilangan bulat, namun polinomial juga dapat memiliki akar rasional, yaitu dengan pecahan. Mari kita lihat bagaimana faktorisasi polinomial jenis ini diselesaikan dengan sebuah contoh:

Faktorkan polinomial tidak lengkap berikut:

$P(x) = 4x^3-7x+3$

Seperti biasa, kami menggunakan aturan Ruffini dengan pembagi suku bebas untuk mencoba menentukan akar polinomial:

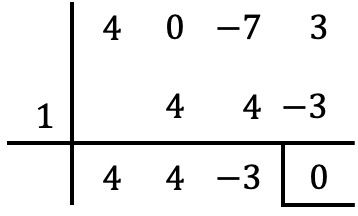
Memfaktorkan polinomial dengan akar rasional

Namun kita tidak dapat menghitung lebih banyak akar dengan Ruffini, karena jika kita mencoba menghitung Ruffini dengan semua bilangan pembagi suku bebas lainnya, kita memperoleh sisa selain nol.

Oleh karena itu, kita mendapati diri kita berada dalam situasi yang hanya ada bersama

$x=1$

sisa pembagiannya setara dengan 0, artinya polinomial tersebut dapat memiliki akar pecahan. Untuk menentukan akar-akar ini kita dapat menerapkan Ruffini dengan pecahan, namun sangat mudah untuk membuat kesalahan dalam perhitungan dan itulah sebabnya dalam kasus ini kami biasanya melakukan hal berikut:

Jika kita tidak dapat melanjutkan penerapan aturan Ruffini dengan akar bilangan bulat, kita harus menetapkan polinomial terakhir yang diperoleh sama dengan 0 dan menyelesaikan persamaan yang dihasilkan. Jadi akar-akar polinomialnya akan menjadi nilai-nilai yang ditemukan dari persamaan tersebut.

Sebaliknya, jika persamaan tidak mempunyai solusi, berarti polinomial tersebut tidak mempunyai akar lagi sehingga tidak dapat difaktorkan seluruhnya.

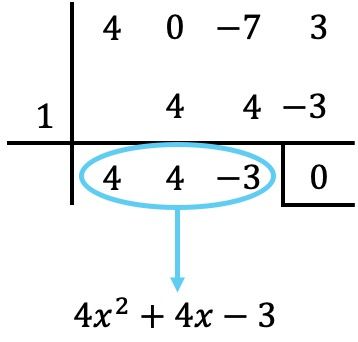
Oleh karena itu, kami menetapkan hasil bagi polinomial sama dengan nol:

$4x^2+4x-3=0$

Dan kami menggunakan rumus persamaan kuadrat untuk menyelesaikan persamaan yang dihasilkan:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-4 \pm \sqrt{4^2-4\cdot 4\cdot (-3)}}{2\cdot 4}= \cfrac{-4\pm \sqrt{16+48}}{8} = \cfrac{-4 \pm\sqrt{64}}{8}$

$\displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}$

Oleh karena itu, akar-akar polinomialnya adalah:

$x=+1 \qquad x=\cfrac{1}{2} \qquad x=-\cfrac{3}{2}$

Oleh karena itu, polinomial memiliki akar dalam bentuk pecahan.

Dan setelah kita mengetahui semua akar polinomial, kita dapat dengan mudah mencari polinomial terfaktor dengan menyatakan setiap akar

$x=a$

dalam bentuk faktor tipenya

$(x-a)$

, artinya untuk setiap akar kata Anda harus memberi tanda kurung dengan a

$x$

dan root telah berubah tanda:

$\displaystyle P(x)= 4\left(x-1\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)$

Ingatlah bahwa untuk memfaktorkan suatu polinomial, Anda juga harus mengalikan faktor-faktornya dengan koefisien suku derajat tertinggi dari polinomial tak terfaktor, yang dalam hal ini adalah 4.

Kasus khusus pemfaktoran polinomial

Biasanya, aturan Ruffini (atau pembagian sintetik) digunakan untuk memfaktorkan polinomial, seperti dijelaskan di atas. Namun bergantung pada polinomial masalahnya, terkadang Anda dapat melakukan pemfaktoran polinomial lebih cepat. Kita akan melihat masing-masing kasus khusus di bawah ini.

Memfaktorkan identitas penting

Jika kita melihat bahwa suatu polinomial berkorespondensi dengan suatu identitas yang terkenal (atau suatu produk yang terkenal), maka sangat mudah untuk memfaktorkannya. Namun, untuk dapat melakukan ini, Anda harus menguasai rumus-rumus identitas terkemuka , jika tidak, saya sarankan Anda melihat tautan ini di mana Anda tidak hanya akan menemukan rumus-rumusnya, tetapi Anda juga dapat melihat contoh-contoh tokoh-tokoh terkemuka. identitas dan Anda bahkan dapat berlatih latihan dengan menyelesaikannya langkah demi langkah.

Perbedaan kuadrat

Seperti yang telah kalian ketahui, rumus identitas penting selisih kuadrat adalah sebagai berikut:

$a^2-b^2=(a+b)\cdot (a-b)$

Oleh karena itu, jika kita menemukan polinomial yang memenuhi ekspresi tersebut

$a^2-b^2$

dapat diperhitungkan secara langsung.

Perhatikan contoh berikut yang memperhitungkan selisih kuadrat:

$x^2-9 = (x+3)(x-3)$

Di sisi lain, akar-akar polinomialnya adalah:

$x=-3 \qquad x=+3$

Contoh lain pemfaktoran binomial yang merupakan selisih kuadrat:

$x^2-4=(x+2)(x-2) \quad \longrightarrow \quad \text{ra\'ices: } x=-2, +2$

$x^2-16=(x+4)(x-4) \quad \longrightarrow \quad \text{ra\'ices: } x=-4, +4$

$x^2-25=(x+5)(x-5) \quad \longrightarrow \quad \text{ra\'ices: } x=-5, +5$

Kotak penjumlahan dan pengurangan

Anda seharusnya sudah mengetahui rumus untuk 2 identitas penting yang tersisa: kuadrat penjumlahan dan kuadrat pengurangan.

Jumlah Persegi

$a^2+2ab+b^2 = (a+b)^2$

Kotak pengurangan

$a^2-2ab+b^2= (a-b)^2$

Jadi, jika kita menyadari bahwa suatu polinomial berhubungan dengan salah satu dari dua identitas penting ini, kita dapat memfaktorkannya secara langsung. Lihatlah contoh berikut:

$x^2+6x+9 = (x+3)^2$

Akar ganda:

$x=-3$

$x^2-8x+16 = (x-4)^2$

Akar ganda:

$x=4$

Mengidentifikasi jenis produk terkenal ini sedikit lebih sulit. Triknya adalah dengan memeriksa apakah suku bebas dari polinomial adalah kuadrat dari suatu bilangan, dan apakah suku dengan derajat yang lebih tinggi adalah kuadrat dari suatu monomial (biasanya

$x$

), dalam hal ini, cukup untuk memverifikasi bahwa itu benar

$2ab$

sama dengan akhir diploma menengah.

Misalnya, jika kita mempunyai polinomial berikut:

$x^2+10x+25$

Dalam hal ini, polinomial tersebut hanya dapat berupa kuadrat dari suatu jumlah, karena semua elemen polinomialnya positif. Jadi variabelnya

$b$

rumusnya harus 5, karena merupakan akar suku bebas dan variabel

$a$

itu pasti

$x$

, karena itu adalah akar dari istilah gelar may.

$a=\sqrt{x^2} = x$

$b=\sqrt{25} = 5$

Yang harus kita lakukan sekarang adalah membuktikan bahwa rumus kuadrat jumlah tersebut terpenuhi dengan suku derajat tengah:

$2ab = 10x \ \color{blue} \bm{?}$

$2ab = 2\cdot x \cdot 5 = 10 x$

✅

Rumus hasil kali penting terpenuhi, sehingga polinomial terfaktornya adalah:

$x^2+10x+25 = (x+5)^2$

Dan akar dari polinomial ini adalah

$x=-5,$

yang merupakan akar ganda karena faktornya dikuadratkan (diulang dua kali).

Di bawah ini adalah contoh-contoh pemfaktoran trinomial kuadrat sempurna:

$x^2-4x+4=(x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+2$

$x^2+14x+49=(x+7)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=-7$

$9x^2-12x+4=(3x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+\cfrac{2}{3}$

Memfaktorkan trinomial derajat kedua

Seperti yang baru saja kita lihat, terkadang ada trinomial yang merupakan kuadrat sempurna dan trinomial ini dapat langsung difaktorkan dengan rumus identitas penting. Namun sebagian besar trinomial bukanlah hasil perkalian yang penting, jadi bagaimana kita memfaktorkan kasus polinomial ini?

Untuk memfaktorkan polinomial kuadrat, tidak perlu menerapkan metode Ruffini, cukup atur polinomialnya menjadi nol dan selesaikan persamaan kuadrat yang dihasilkan. Oleh karena itu, solusi persamaan tersebut akan menjadi akar-akar polinomial.

Misalnya, jika kita diminta memfaktorkan polinomial berderajat 2 berikut:

$P(x) = x^2+2x-15$

Daripada menggunakan Ruffini, kami menetapkan polinomialnya sama dengan 0:

$x^2+2x-15=0$

Dan sekarang kita menggunakan rumus persamaan derajat 2 untuk mencari solusi persamaan tersebut:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-2 \pm \sqrt{2^2-4\cdot 1\cdot (-15)}}{2\cdot 1}= \cfrac{-2\pm \sqrt{4+60}}{2} = \cfrac{-2 \pm\sqrt{64}}{2}$

$\displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}$

Oleh karena itu, akar-akar polinomialnya adalah:

$x=3 \qquad x=-5$

Dan terakhir, faktorisasi polinomialnya adalah:

$P(x) =(x-3)(x+5)$

Memfaktorkan trinomial derajat keempat dengan eksponen genap

Seperti pada kasus sebelumnya, untuk memfaktorkan polinomial derajat keempat dengan eksponen genap, kita perlu mengatur polinomialnya sama dengan nol dan menyelesaikan persamaan bikuadrat. Sehingga nilai yang ditemukan sesuai dengan akar polinomialnya.

Sebagai contoh, kita akan memfaktorkan polinomial berderajat 4 berikut:

$P(x) =x^4-5x^2+4$

Pertama, kita atur polinomialnya sama dengan nol:

$x^4-5x^2+4=0$

Sekarang kita perlu menyelesaikan persamaan bikuadrat. Untuk melakukan ini, kami membuat perubahan variabel:

$x^2=t$

$t^2-5t+4=0$

Kita selesaikan persamaan kuadrat dengan rumus:

$t= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$t= \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1}= \cfrac{5\pm \sqrt{25-16}}{2} = \cfrac{5 \pm\sqrt{9}}{2}$

$\displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}$

Kami membatalkan perubahan variabel untuk menghitung akar:

$x^2=t$

$x^2=4$

$x=\sqrt{4}$

$x=\pm 2$

$x^2=1$

$x=\sqrt{1}$

$x=\pm 1$

Oleh karena itu, akar-akar polinomialnya adalah:

$x=+2 \qquad x=-2 \qquad x=+1 \qquad x=-1$

Dan setelah kita mengetahui akar atau nol suatu polinomial, kita memfaktorkannya dengan menyatakan akar-akarnya secara aljabar dalam bentuk faktor:

$P(x) =(x-1)(x+1)(x-2)(x+2)$

Memfaktorkan polinomial dengan mengelompokkan

Dalam beberapa kasus yang sangat khusus, suatu rumus dapat digunakan untuk memfaktorkan suatu jenis polinomial yang sangat khusus.

Jika kita mempunyai polinomial dengan bentuk berikut:

$x^2-ax- bx+ab$

Kita dapat menyederhanakan polinomial dengan menghilangkan faktor persekutuannya:

$x^2-ax- bx+ab = x(x-a)-b(x-a)$

Dan polinomialnya dapat disederhanakan lebih lanjut dengan mengekstraksi faktor persekutuannya untuk kedua kalinya:

$x(x-a)-b(x-a) =(x-a)\cdot (x-b)$

Dengan cara ini kami dapat memfaktorkan polinomial tanpa menerapkan Ruffini atau metode lainnya. Dan akar dari polinomial tersebut adalah:

$x=a \qquad x=b$

Sekarang mari kita lihat metode ini dengan contoh numerik:

$x^2-3x-2x+6$

Pertama, kita hapus faktor persekutuannya dengan

$x$

dan dengan 2:

$x^2-3x-2x+6 = x(x-3)-2(x-3)$

Dan seperti sekarang

$(x-3)$

adalah faktor persekutuan dari polinomial, kita mengekstrak faktor persekutuannya

$(x-3):$

$x(x-3)-2(x-3)=(x-3)\cdot (x-2)$

Oleh karena itu, akar-akar polinomialnya adalah:

$x=3 \qquad x=2$

Metode ini disebut juga faktorisasi polinomial dengan ekstraksi faktor persekutuan ganda. Meskipun ini merupakan prosedur yang sangat cepat, kami tidak menyarankan melakukan jenis faktorisasi ini karena kesalahan sering dilaporkan saat memfaktorkan dengan metode ini. Selain itu, seperti yang kita lihat di atas, polinomial berderajat 2 juga dapat difaktorkan dengan menyelesaikan persamaan kuadrat sederhana. Singkatnya, tidak akan terjadi apa-apa jika Anda tidak memahami metode ini dengan baik.

Terakhir, perlu diperhatikan bahwa masih ada metode faktorisasi polinomial lain yang lebih kompleks, seperti algoritma LLL, metode Kronecker, dan metode Trager, yang tidak dijelaskan di sini karena kesulitan matematisnya.

Latihan soal pemfaktoran polinomial

Setelah Anda melihat semua jenis pemfaktoran polinomial, kami menyarankan Anda berlatih mencoba menyelesaikan latihan. Inilah sebabnya kami telah menyiapkan beberapa latihan langkah demi langkah untuk memfaktorkan polinomial di bawah ini. Ingatlah bahwa jika Anda memiliki pertanyaan, Anda dapat menulisnya di komentar dan kami akan menjawabnya dengan cepat.

Latihan 1

Lakukan faktorisasi polinomial derajat 3 berikut:

$P(x)=x^3-3x^2-6x+8$

Lihat solusinya

Ini adalah polinomial yang lengkap, teratur, derajat ketiga dan akhirnya independen. Oleh karena itu, kami menerapkan metode Ruffini untuk menentukan akar-akar polinomial:

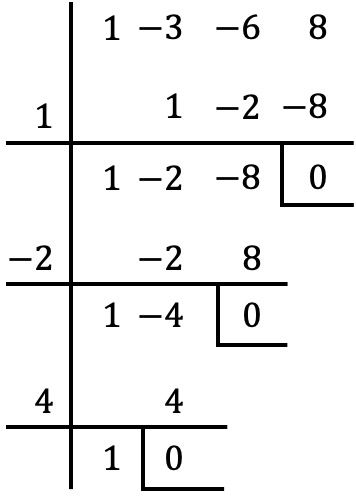
latihan langkah demi langkah untuk memfaktorkan polinomial

Oleh karena itu, akar polinomialnya adalah sebagai berikut:

$x=+1 \qquad x=-2 \qquad x=+4$

Oleh karena itu, faktorisasi polinomialnya adalah:

$P(x)= 1 \cdot (x-1)\cdot (x+2) \cdot (x-4)$

$\bm{P(x)= (x-1)(x+2)(x-4)}$

Latihan 2

Hitung faktorisasi polinomial derajat 4 berikut:

$P(x)=x^4+x^3-7x^2-x+6$

Lihat solusinya

Ini adalah polinomial derajat keempat dan dengan suku independen, oleh karena itu kami menggunakan metode Ruffini untuk mencari akar polinomial tersebut:

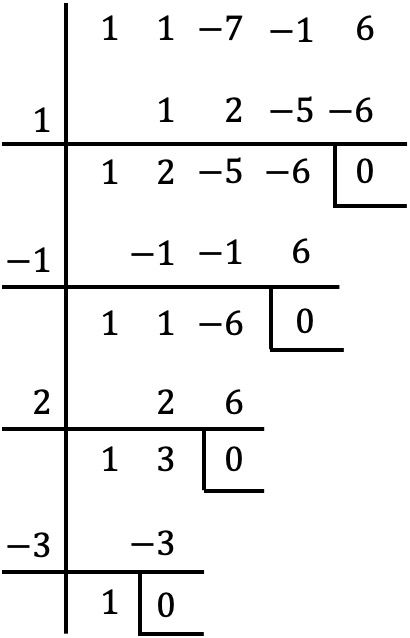
Oleh karena itu, akar-akar polinomialnya adalah:

$x=+1 \qquad x=-1 \qquad x=2 \qquad x=-3$

Dan ketika kita memfaktorkan polinomialnya, kita mendapatkan:

$P(x)= 1 \cdot (x-1)\cdot (x+1)\cdot (x-2) \cdot (x+3)$

$\bm{P(x)= (x-1)(x+1)(x-2)(x+3)}$

Latihan 3

Tentukan faktorisasi polinomial derajat empat berikut:

$P(x)=x^4-2x^3-13x^2-10x$

Lihat solusinya

Dalam hal ini polinomial tidak memiliki suku bebas, pertama-tama kita harus mengekstrak faktor persekutuannya:

$P(x)=x(x^3-2x^2-13x-10)$

Sekarang kita telah mengambil faktor persekutuan dari x, kita menghitung akar atau nol dari polinomial dalam tanda kurung menggunakan metode Ruffini:

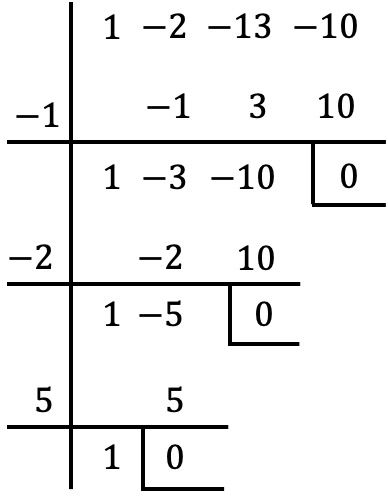
latihan faktorisasi polinomial Ruffini pdf

Jadi akar-akar polinomial adalah akar-akar yang kita temukan dengan metode Ruffini ditambah x=0 dari faktor persekutuan:

$x=0 \qquad x=-1 \qquad x=-2 \qquad x=5$

Dan terakhir, dengan menguraikan polinomial menjadi faktor-faktor, kita memperoleh ekspresi berikut:

$P(x)= 1 \cdot x \cdot (x+1)\cdot (x+2)\cdot (x-5)$

$\bm{P(x)= x(x+1)(x+2)(x-5)}$

Latihan 4

Ubah polinomial derajat ketiga berikut menjadi faktor:

$P(x)=6x^3+25x^2+21x-10$

Lihat solusinya

Polinomial ini memiliki suku independen, oleh karena itu kami menghitung akar-akarnya dengan algoritma Ruffini:

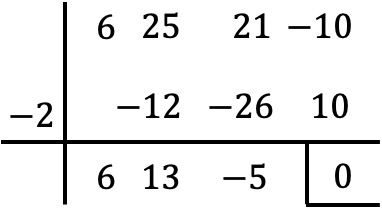
polinomial faktorial derajat 3 pada baris 2

Namun, ketika kita mencapai titik ini, kita tidak dapat terus menerapkan aturan Ruffini, karena tanpa bilangan bulat lain, sisa pembagiannya adalah nol.

Oleh karena itu, kami menetapkan polinomial yang dihasilkan sama dengan nol:

$6x^2+13x-5=0$

Dan kami menerapkan rumus persamaan kuadrat untuk menyelesaikan persamaan yang dihasilkan:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-13 \pm \sqrt{13^2-4\cdot 6\cdot (-5)}}{2\cdot 6}= \cfrac{-13\pm \sqrt{169+120}}{12} = \cfrac{-13 \pm\sqrt{289}}{12}$

$\displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}$

Oleh karena itu, akar atau nol dari polinomial tersebut adalah:

$x=-2 \qquad x=\cfrac{1}{3} \qquad x=-\cfrac{5}{2}$

Jadi faktorisasi polinomial harus dilakukan dengan pecahan:

$\displaystyle P(x)= 6\left(x+2\right)\left(x-\frac{1}{3}\right)\left(x+\frac{5}{2}\right)$

Latihan 5

Tentukan faktorisasi polinomial derajat 6 berikut:

$P(x)=x^6-3x^5+14x^3-12x^2$

Lihat solusinya

Polinomial dalam soal tidak memiliki suku independen, jadi pertama-tama kita harus mengekstrak faktor persekutuannya, yang dalam hal ini adalah

$x^2:$

$P(x)=x^2(x^4-3x^3+14x-12)$

Dan setelah kita menghilangkan faktor persekutuan dari polinomial tersebut, kita mencari akar-akar polinomial tersebut di dalam tanda kurung menggunakan aturan Ruffini:

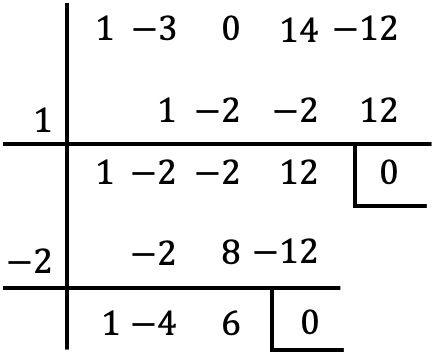
Namun ketika kita sudah sampai pada tahap ini, kita tidak bisa terus bergerak maju, karena tanpa bilangan bulat lainnya, sisanya adalah nol.

Oleh karena itu kami menetapkan polinomial yang diperoleh sama dengan nol:

$x^2-4x+6=0$

Dan kita selesaikan persamaan kuadrat tersebut dengan rumus:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1\cdot 6}}{2\cdot 1}= \cfrac{4\pm \sqrt{16-24}}{2} = \cfrac{4 \pm\sqrt{-8}}{2} \ \color{red} \bm{\times}$

Tidak ada akar bilangan negatif, sehingga persamaan tersebut tidak memiliki solusi, yang berarti kita tidak dapat menemukan akar polinomial lainnya. Dengan kata lain, polinomial tersebut tidak dapat difaktorkan sepenuhnya.

Namun, akar yang dapat kami temukan adalah:

$x=0 \qquad x=0 \qquad x=1 \qquad x=-2$

Perhatikan bahwa akarnya

$x=0$

diulang dua kali karena kita menghilangkan faktor persekutuannya

$x^2,$

dan karena berbentuk kuadrat, berarti akarnya ganda.

Kesimpulannya, polinomial yang difaktorkan adalah hasil kali semua akar-akar yang ditemukan, dinyatakan sebagai faktor

$(x-a)$

dikalikan dengan polinomial yang diperoleh dari aturan Ruffini yang tidak dapat diperhitungkan lebih lanjut:

$P(x)= 1 \cdot x^2 \cdot (x-1)\cdot (x+2)\cdot (x^2-4x+6)$

$\bm{P(x)= x^2(x-1)(x+2)(x^2-4x+6)}$

Latihan 6

Lakukan faktorisasi semua polinomial berikut:

$\text{A)} \ P(x)=x^2 + 12x+36$

$\text{B)} \ Q(x)=x^2 -64$

$\text{C)} \ R(x)=x^2 - 18x+81$

$\text{D)} \ S(x)=x^2+10x+24$

Lihat solusinya

Polinomial di bagian A) sesuai dengan identitas penting, terutama kuadrat jumlah tersebut. Oleh karena itu, faktorisasinya adalah:

$P(x)=x^2 + 12x+36 = \bm{(x+6)^2}$

Polinomial bagian B) juga merupakan hasil kali yang menonjol, khususnya selisih kuadratnya, oleh karena itu:

$Q(x)=x^2 -64 = \bm{(x+8)(x-8)}$

Demikian pula, polinomial di bagian C) adalah persamaan yang penting, khususnya terdiri dari kuadrat pengurangan. Oleh karena itu, faktorisasinya adalah:

$R(x)=x^2 - 18x+81 = \bm{(x-9)^2}$

Terakhir, polinomial pada bagian D) bukanlah identitas yang menonjol. Oleh karena itu, kita harus mengatur polinomialnya menjadi 0 dan menyelesaikan persamaan yang dihasilkan untuk menemukan akar-akarnya:

$x^2+10x+24 =0$

Kami menggunakan rumus persamaan kuadrat:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-10 \pm \sqrt{10^2-4\cdot 1\cdot 24}}{2\cdot 1}= \cfrac{-10\pm \sqrt{100-96}}{2} = \cfrac{-10 \pm\sqrt{4}}{2}$

$\displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}$

Oleh karena itu, akar-akar polinomial D) adalah:

$x=-4 \qquad x=-6$

Dan terakhir, hasil faktorisasi polinomialnya adalah:

$\bm{S(x)=(x+4)(x+6)}$

Cara memfaktorkan polinomial (polynomial factoring)

Apa itu faktorisasi polinomial?

Cara memfaktorkan polinomial dengan aturan Ruffini

Memfaktorkan polinomial tanpa suku bebas

Memfaktorkan polinomial dengan akar rasional

Kasus khusus pemfaktoran polinomial

Memfaktorkan identitas penting

Perbedaan kuadrat

Kotak penjumlahan dan pengurangan

Memfaktorkan trinomial derajat kedua

Memfaktorkan trinomial derajat keempat dengan eksponen genap

Memfaktorkan polinomial dengan mengelompokkan

Latihan soal pemfaktoran polinomial

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Latihan 5

Latihan 6

Tinggalkan Komentar Batalkan Balasan