Di halaman ini Anda akan menemukan penjelasan tentang matriks-matriks sejenis, disebut juga matriks-matriks sejenis. Selain itu, kami tunjukkan contoh jelas dari dua matriks serupa dan semua properti dari matriks jenis ini sehingga Anda tidak perlu ragu. Terakhir, Anda bahkan dapat melihat hubungannya dengan matriks-matriks yang kongruen.
Apa yang dimaksud dengan matriks serupa (atau serupa)?
Pengertian matriks sejenis adalah sebagai berikut:
dua matriks
![]()
Dan
![]()
serupa (atau serupa) jika terdapat matriks
![]()
yang memenuhi kondisi berikut:
![]()
Atau setara:
![]()
Faktanya, matriks
![]()
bertindak sebagai matriks perubahan basis. Oleh karena itu, yang dimaksud dengan persamaan ini adalah matriks
![]()
dapat dinyatakan dalam basis lain (
![]()
), yang memunculkan matriks
![]()
.
Istilah ini juga bisa disebut transformasi kesamaan , karena kita sebenarnya mentransformasikan matriks
![]()
dalam matriks
![]()
.
Jelas matriksnya
![]()
matriks tersebut harus berupa matriks beraturan atau tidak berdegenerasi (determinan bukan nol).
Di sisi lain, kita dapat menunjukkan bahwa dua matriks serupa dengan ekspresi berikut:
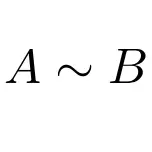
Kelas matriks ini lebih penting daripada yang terlihat pada aljabar linier. Mereka terutama digunakan untuk matriks yang dapat didiagonalisasi, karena prosedur untuk mendiagonalisasi matriks apa pun didasarkan pada konsep kesamaan matriks.
Faktanya, proses mendiagonalisasi suatu matriks melibatkan penghitungan matriks serupa yang sekaligus merupakan matriks diagonal. Anda dapat melihat cara melakukannya di cara mendiagonalisasi matriks .
Contoh matriks sejenis atau sejenis
Kemudian kita akan melihat contoh matriks serupa berdimensi 2×2 untuk menyelesaikan asimilasi konsepnya.
- Matriks persegi A dan B sebangun satu sama lain melalui matriks inversi P:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4978e1117b69063b63256a0663eaf207_l3.png)
![Rendered by QuickLaTeX.com \displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6344f1d5a14dd381ab105bcb52827455_l3.png)
Untuk menunjukkan bahwa matriks-matriks tersebut saling sebangun, pertama-tama kita harus menghitung invers matriks dari P:
![Rendered by QuickLaTeX.com \displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49a4a995246e782635e2e2b43302798_l3.png)
Dan sekarang kita memeriksa kemiripannya dengan melakukan perkalian matriks yang mendefinisikan kemiripan dua matriks:
![]()
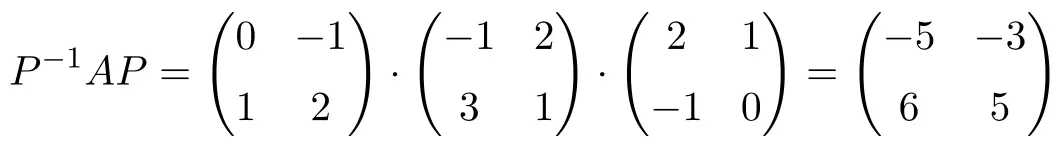
![]()
✅
Ya, relasi kemiripannya terpenuhi, jadi matriks-matriksnya sebangun.
Properti matriks serupa
Dua matriks A dan B yang serupa mempunyai ciri-ciri sebagai berikut:
- Pangkat yang sama.
![]()
- determinan kedua matriks tersebut sama.
![]()
- Pelacakan yang sama.
![]()
- Nilai eigen (atau nilai eigen) yang sama. Namun, vektor eigen (atau vektor eigen) biasanya berbeda.
- Polinomial karakteristik dan polinomial minimum yang sama.
- Transposisi suatu matriks mirip dengan matriks aslinya.
- Matriks B dapat dicari dengan menerapkan operasi elementer pada baris-baris matriks A, dan sebaliknya.
- Jelas sekali kemiripannya tercermin. Artinya, jika A mirip dengan B, maka B juga mirip dengan A.
- Selain itu, kemiripan matriks juga bersifat simetris. Dengan kata lain, jika dengan matriks P dapat diperoleh matriks yang sebangun dengan A (B), maka matriks yang sebangun dengan B (A) juga dapat diperoleh dengan matriks P yang sama:
![]()
![]()
- Selain itu, kesamaan bersifat transitif. Jadi jika matriks A sebangun dengan matriks B dan matriks B sebangun dengan matriks C, maka matriks A juga sebangun dengan matriks C.
![Rendered by QuickLaTeX.com \left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9f845ee4a4c9e72220ecb4033ea9640_l3.png)
- Terakhir, setiap dadu mirip dengan dadu gigi gergaji. Dan dari sifat ini kita dapat menyimpulkan akibat wajar berikut: setiap matriks persegi sebangun dengan matriks segitiga.
matriks yang kongruen
Di sisi lain, ada juga hubungan lain yang sangat mirip antara matriks, tetapi bukan dengan matriks invers, melainkan dengan matriks transpos. Ini disebut kongruensi .
Dua matriks A dan B kongruen jika terdapat matriks P yang dapat dibalik dan memenuhi persamaan berikut:
![]()
Seperti yang Anda lihat, ini adalah analog dari matriks serupa tetapi matriksnya ditransposisikan.